经典DP - 走方格

不同路径的数目(一)_牛客题霸_牛客网

状态：

子状态：从(0,0) 到达 (1,0),(1,1),(2,1),...(m-1,n-1) 的路径数

F(i,j): 从 (0,0) 到达 F(i,j) 的路径数

状态递推：

F(i,j) = F(i-1,j) + F(i,j-1)

初始化：

特殊情况：第0 行和第 0 列

F(0,i) = 1

F(i,0) = 1

返回结果：

F(m-1,n-1)


class Solution {
public:

    int uniquePaths(int m, int n) {
        if(m<1||n<1) return 0;

        vector<vector<int>> ret(m,vector<int>(n,1));

        for(int i=1;i<m;i++)
            for(int j=1;j<n;j++) 
                ret[i][j]=ret[i-1][j]+ret[i][j-1];
        return ret[m-1][n-1];
    }
};

走方格2.0

带权值的最小路径和_牛客题霸_牛客网

状态：

        子状态：从(0,0) 到达 (1,0),(1,1),(2,1),...(m-1,n-1) 的最短路径

        F(i,j): 从 (0,0) 到达 F(i,j) 的最短路径

状态递推：

        F(i,j) = min{F(i-1,j) , F(i,j-1)} + (i,j)

初始化：

        F(0,0) = (0,0)

        特殊情况：第0 行和第 0 列

        F(0,i) = F(0,i-1) + (0,i)

        F(i,0) = F(i-1,0) + (i,0)

返回结果：

        F(m-1,n-1)


class Solution {
public:

    int minPathSum(vector<vector<int> >& grid) {
        if(grid.empty()||grid[0].empty()) return 0;

        int m=grid.size();
        int n=grid[0].size();
        vector<vector<int>> ret(m,vector<int>(n,0));

        ret[0][0]=grid[0][0];
        for(int i=1;i!=m;i++) ret[i][0]=ret[i-1][0]+grid[i][0];
        for(int i=1;i!=n;i++) ret[0][i]=ret[0][i-1]+grid[0][i];

        for(int i=1;i<m;i++)
            for(int j=1;j<n;j++){
                ret[i][j]=min(ret[i-1][j],ret[i][j-1])+grid[i][j];
            }
        return ret[m-1][n-1];
    }
};

分割回文串

分割回文串-ii_牛客题霸_牛客网

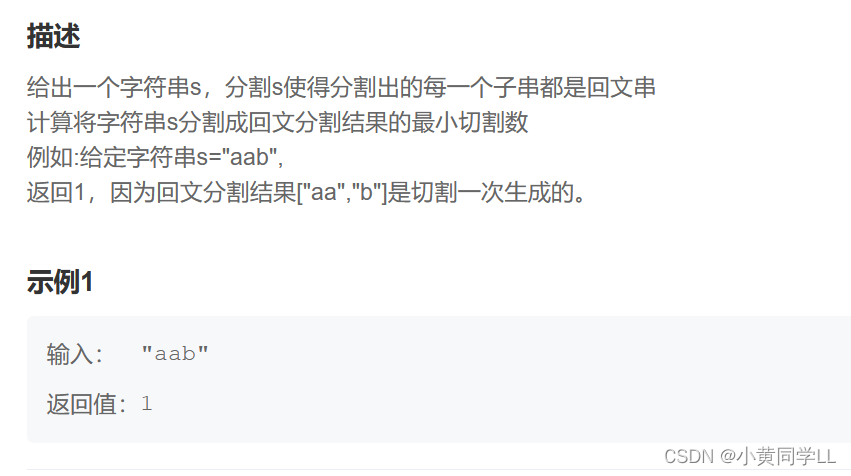
状态：

        子状态：到第1,2,3,...,n 个字符需要的最小分割数

        F(i): 到第 i个字符需要的最小分割数

状态递推：

        F(i) = min{F(i), 1 + F(j)}, 当 j<i && j+1到 i 是回文串时

        上式表示如果从j+1 到 i 判断为回文字符串，且已经知道从第 1 个字符

        到第j 个字符的最小切割数，那么只需要再切一次，就可以保证

        1-->j, j+1-->i都为回文串。

初始化：

        F(i) = i - 1

        上式表示到第i 个字符需要的最大分割数

        比如单个字符只需要切0 次，因为单子符都为回文串

        2个字符最大需要 1 次， 3 个 2 次 ......

返回结果：

        F(n)

举个栗子：对于字符串"aabaa",对于当 j<i && j+1到i是回文串才更新的情况

f[0]=-1;则字符串“a”有min（f[1]，1+f[0]）==0;

对字符串“aa”有min（f[2]，1+f[0]）==min（1,0）==0；

对字符串“aab”有min（f[3]，1+f[1]）==min（2,1）==1；

对字符串“aaba”有min（f[4]，1+f[1]）==min（3,1）==1；（a|aba）

.......

沿途会遍历所有分割方法，取最小值

class Solution {
  public:
    int minCut(string s) {
        if (s.empty()) return 0;
        int len = s.size();
        vector<int> cut;
        // F(i)初始化
        // F(0）= -1，必要项，如果没有这一项，对于重叠字符串“aaaaa”会产生错误的结果
        for (int i = 0; i < 1 + len; ++i) {
            cut.push_back(i - 1);
            //最大分割数随字符增加
        }
        for (int i = 1; i < 1 + len; ++i) {
            for (int j = 0; j < i; ++j) {
                // F(i) = min{F(i), 1 + F(j)}, 当 j<i && j+1到i是回文串才更新
                if (isPalindrome(s, j, i - 1)) {
                    cut[i] = min(cut[i], 1 + cut[j]);
                }
            }
        }
        return cut[len];
    }
    //判断是否回文串
    bool isPalindrome(string s, int i, int j) {
        while (i < j) {
            if (s[i] != s[j]) {
                return false;
            }
            i++;
            j--;
        }
        return true;
    }
};

上述方法两次循环时间复杂度是 O(n^2),

判断回文串时间复杂度是 O(n),

所以总时间复杂度为 O(n^3)

对于过长的字符串，在 OJ 的时候会出现 TLE(Time Limit Exceeded)

分割回文串 - 回文优化

状态：

        从第一个字符到第二个字符是不是回文串，第1-3 ，第 2-5 ， ...

        F(i,j): 字符区间 [i,j] 是否为回文串

状态递推：

        F(i,j): true->{s[i]==s[j] && F(i+1,j-1)} 否则false

        上式表示如果字符区间首尾字符相同且在去掉区间首尾字符后字符区间仍为回文串，

        则原字符区间为回文串

        从递推公式中可以看到第i 处需要用到第 i+1 处的信息，所以 i 应该从字符串末尾遍历

初始化：

        F(i,j) = false

返回结果：

        矩阵F(n,n), 只更新一半值（ i <= j）， n^2 / 2

举个栗子：

我们看递推公式发现 true->{s[i]==s[j] && F(i+1,j-1)}更新所需要的状态是下一行的前一列，也就是说要从下往上更新

for (int i = len - 1; i >= 0; --i) {//从最后一行开始更新
    for (int j = i; j < len; ++j) {
        if (j == i) {
        // 一个字符
            mat[i][j] = true;
        } 
        else if (j == i + 1) {
        // 只有两个
            mat[i][j] = (s[i] == s[j]);
        } 
        else {
            mat[i][j] = ((s[i] == s[j]) && mat[i + 1][j - 1]);
        }
    }

class Solution {
  public:
    int minCut(string s) {
        if (s.empty()) return 0;
        int len = s.size();
        vector<int> cut;
        for (int i = 0; i < 1 + len; ++i) {
            cut.push_back(i - 1);
        }

        vector<vector<bool> > mat = getMat(s);//dp回文串

        for (int i = 1; i < 1 + len; ++i) {
            for (int j = 0; j < i; ++j) {
                if (mat[j][i - 1]) {
                    cut[i] = min(cut[i], 1 + cut[j]);
                }
            }
        }
        return cut[len];
    }
    vector<vector<bool> > getMat(string s) {
        int len = s.size();
        vector<vector<bool> > mat = vector<vector<bool> >(len, vector<bool>(len,
                                    false));
        for (int i = len - 1; i >= 0; --i) {
            for (int j = i; j < len; ++j) {
                if (j == i) mat[i][j] = true;
                else if (j == i + 1) mat[i][j] = (s[i] == s[j]);
                else mat[i][j] = ((s[i] == s[j]) && mat[i + 1][j - 1]);
                
            }
        }
        return mat;
    }
};

判断回文串的方法可以继续优化，使总体时间复杂度将为O(n^2)