新的时期,人力资源和社会保障事业进入新一轮的制度创新和加快发展阶段。把对各项人力资源和社会保障业务的支持和服务纳入信息化建设,通过 “数字人社”信息化建设项目,是充分利用新一代信息技术,有效整合各类信息资源,持续推动市人社信息化建设、支撑人社事业发展的有效途径;有利于促进人社业务精细化管理,促进公共服务均等化、普惠性和可及性,打通服务群众“最后一公里”,增强群众对政府公共服务的获得感、认同度和满意度。可为创新市人力资源和社会保障工作长效机制奠定基础。
4月24日,人社部规财司司长张立新调研成都高新区中和街道、成都市武侯区晋阳街道人社公共服务标准化工作。

成都高新区中和街道


成都市武侯区晋阳街道
值得一提的是,本次参观的两处街道均有璞华技术加持。其中,璞华为成都高新区中和街道提供仲裁智能化服务,助力成都市武侯区晋阳街道实现人社标准化。
成都高新区
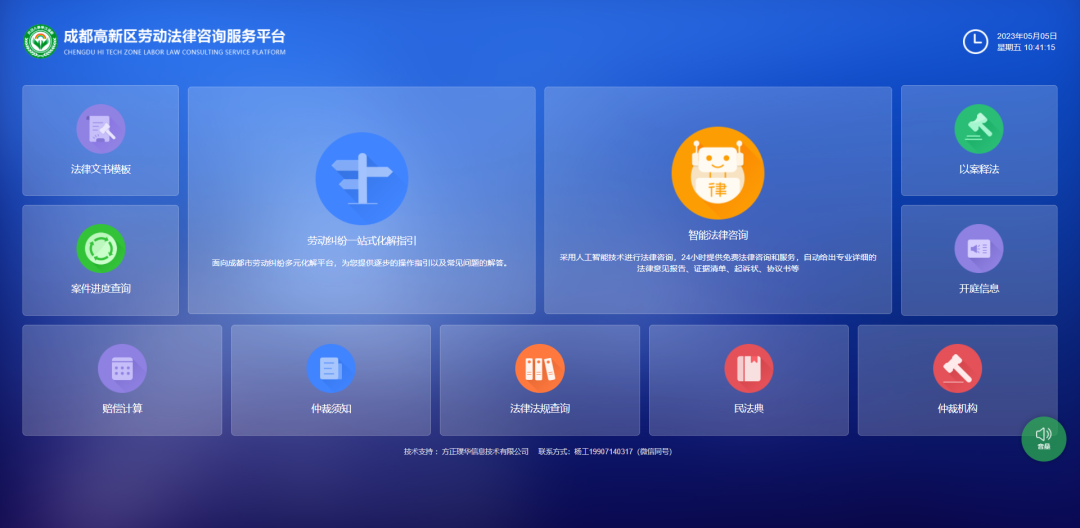
依托璞华仲裁智慧树,成都高新区劳动人事争议仲裁信息管理平台通过信息化、标准化、智能化的办案系统,实现对仲裁案件的全程跟踪和管理。同时达成了和成都高新区办案系统联动,把单个机制的效用发挥到极致,当事人不仅可以通过平台查看近期开庭一览,还可以查询办案进度和体验各类辅助功能。
“及时有效的权益维护让广大劳动者获得感、幸福感、安全感更加充实、更有保障、更可持续。”成都高新区人社厅相关负责人介绍。各项举措有效拓宽了当事人维权渠道,不断提高劳动争议处理质效,更让当事人在每一起案件中都能感受到公平正义。
通过科技赋能,璞华携手成都高新区做到完善办案机制和提升办案能力同频共振、同向发力,促进成都高新区人社体系办案水平提升确保办案质效提升!
成都市武侯区


2023年4月20日,璞华“人社综合服务自助平台”在成都市武侯区晋阳街道便民中心落地,作为武侯人社新的服务触点正式开始提供服务。
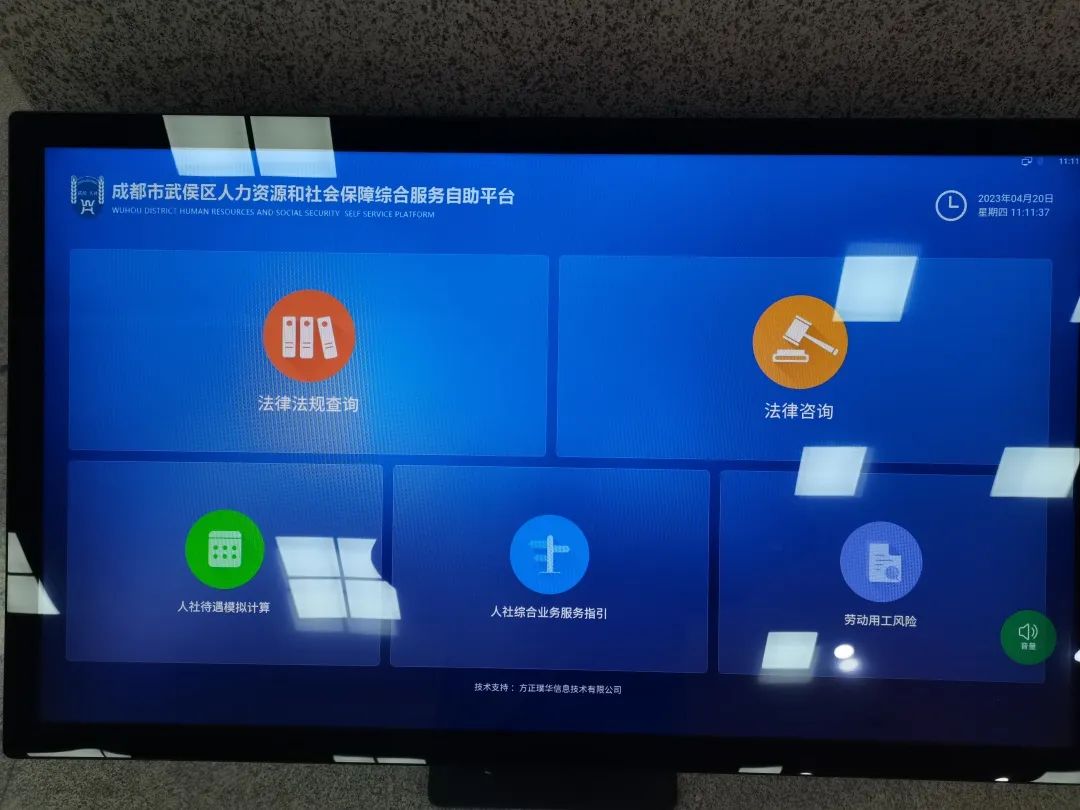
人社综合咨询服务自助平台创新嵌入同标准待遇计算公式及领取标准,提供人社法律综合咨询、相关待遇计算、业务办理一次性告知书查询推送等多元服务,满足“标准明、看得懂、算得清”人社政策的需求,以多样化应用功能赋能人社领域基本公共服务标准化建设,满足群众近距离享受人社便捷化、标准化服务的需求。
璞华积极投身人社行业信息化建设
自2016年以来,璞华基于在仲裁领域的丰富实践经验为贵州、四川、湖北等各地人社信息化建设提供多维度的技术服务支撑,不仅满足多地区、多层级、多业务的需要,助力全省人社一体化、业务在线化、治理数据化、服务智能化奠定了坚实基础,以技术为根基服务人社体系信息化、智能化、智慧化的发展。
近年来,璞华更是积极投身人社行业建设,在提供先进技术和优秀产品的同时,组建了专业、稳定的行业服务团队,并与合作伙伴通力协作,打造出全面智能的劳动人事法律自助咨询服务平台解决方案,助力人社行业智慧化升级驶入快车道。
未来,璞华将继续携手产业链生态伙伴共同深入探索人社行业信息化、数字化、智能化建设,持续完善人社行业产品,助力政务服务水平更上一层楼。