题目链接

P3865 ST 表

题目描述

这是一道 ST 表经典题——静态区间最大值

请注意最大数据时限只有 0.8s，数据强度不低，请务必保证你的每次查询复杂度为 $O(1)$。若使用更高时间复杂度算法不保证能通过。

如果您认为您的代码时间复杂度正确但是 TLE，可以尝试使用快速读入：

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

函数返回值为读入的第一个整数。

快速读入作用仅为加快读入，并非强制使用。

题目描述

给定一个长度为 $N$ 的数列，和 $ M $ 次询问，求出每一次询问的区间内数字的最大值。

输入格式

第一行包含两个整数 $N,M$，分别表示数列的长度和询问的个数。

第二行包含 $N$ 个整数（记为 $a_i$），依次表示数列的第 $i$ 项。

接下来 $M$ 行，每行包含两个整数 $l_i,r_i$，表示查询的区间为 $[l_i,r_i]$。

输出格式

输出包含 $M$ 行，每行一个整数，依次表示每一次询问的结果。

样例 #1

样例输入 #1

8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8

样例输出 #1

9
9
7
7
9
8
7
9

提示

对于 $30\%$ 的数据，满足 $1\le N,M\le 10$。

对于 $70\%$ 的数据，满足 $1\le N,M\le {10}^5$。

对于 $100\%$ 的数据，满足 $1\le N\le {10}^5$，$1\le M\le 2\times {10}^6$，$a_i\in [0,{10}^9]$，$1\le l_i\le r_i\le N$。

算法思想：ST表

先来了解几个概念：倍增，ST表，RMQ

倍增

倍增就是成倍增加。若问题的状态空间特别大，则一步步递推求解时间复杂度太高，可以通过倍增的思想，只考察$2$的整数次幂位置，$2,4,\mathrm{8...}$，快速缩小求解范围，知道找到解。

ST表

ST(Sparse Table，稀疏表)算法采用了倍增的思想，在$O(nlogn)$时间里构造一个二维表，可以在$O(1)$的时间查找$[L,R]$区间的最值，即RMQ(Range Minimum/Maximum Query)问题。

基本原理

设$f[i,j]$表示区间$[i,i+2^j-1]$的最值，即从$i$开始，长度为$2^j$的区间的最大值或者最小值，如下图所示：

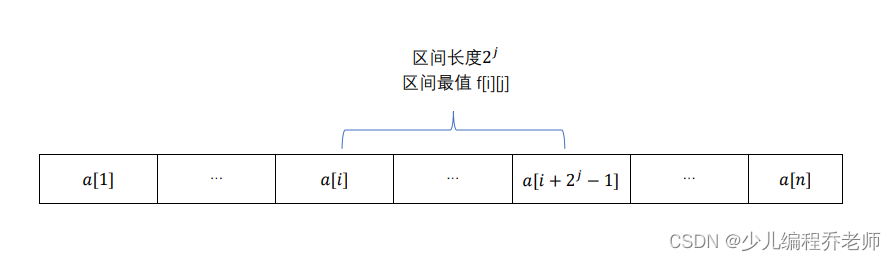
长度为$2^j$的区间可以被分成两个长度为$2^{j-1}$的子区间，然后可以得到递推公式： f [ i ] [ j ] = m a x { f [ i , j − 1 ] , f [ i + 2 j − 1 , j − 1 ] } f[i][j]=max\{f[i,j-1],f[i+2^{j-1},j-1]\} f[i][j]=max{f[i,j−1],f[i+2j−1,j−1]}。如下图所示：

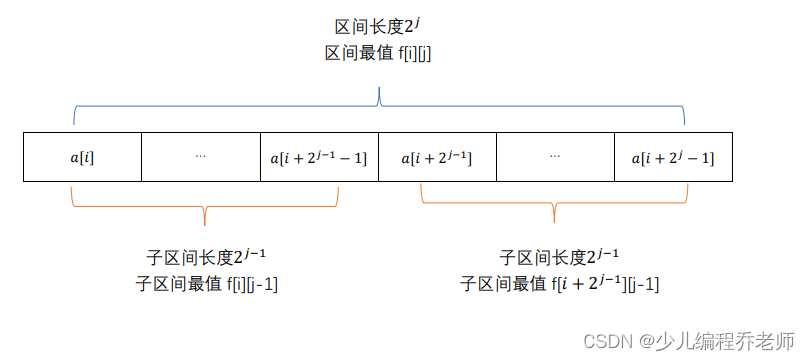
创建ST表

$f[i,j]$表示区间$[i,i+2^j-1]$的最值，区间长度为$2^j$，若数组的长度$n$，最大区间长度$2^j\le n$，则$j\le \lfloor lo{g}_{2}n\rfloor$。

void create() {
    //初始状态
    //f[i][0]表示从i开始长度为2^0的区间最值为a[i]本身
    for(int i = 1; i <= n; i ++) f[i][0] = a[i];
    int k = log2(n);
    //枚举区间长度的指数j
    for(int j = 1; j <= k; j ++)
        for(int i = 1; i + (1 << j) - 1 <= n; i ++)
            f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}

例如，有10个元素的数组 a [ 1...10 ] = { 5 , 3 , 2 , 7 , 9 , 8 , 10 , 1 , 3 , 15 } a[1...10]=\{5,3,2,7,9, 8,10,1,3,15\} a[1...10]={5,3,2,7,9,8,10,1,3,15}

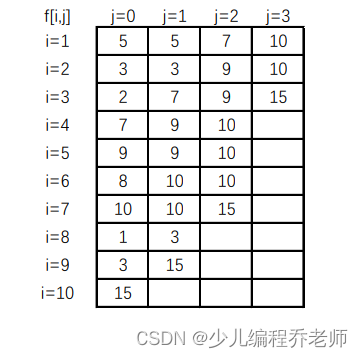
查询ST表

查询区间$[L,R]$的最值，首先需要计算的区间长度为$R-L+1$，那么$2^j\le R-L+1$，因此设$j=lo{g}_2(R-L+1)$。
那么要查询区间$[L,R]$的最值，则可以将查询区间分为两个，取两个区间的最值即可。这两个区间分别为：

• 从$L$向后的$2^j$个数
• 从$R$向前的$2^j$个数

这两个区间可能有重叠，但对求最值没有影响。

//利用ST表查询区间[L,R]的最大值
int query(int L, int R) {
    int j = log2(R - L + 1);
    return max(f[L][j], f[R - (1 << j) + 1][j]);
}

时间复杂度

• 创建ST表：$O(nlogn)$
• 查询ST表：$O(1)$

代码实现

#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 1e5 + 10, M = 100;
int n, a[N], f[N][M];
//创建ST表
void create() {
    //初始状态
    //f[i][0]表示从i开始长度为2^0的区间最值为a[i]本身
    for(int i = 1; i <= n; i ++) f[i][0] = a[i];
    int k = log2(n);
    //枚举区间长度指数j
    for(int j = 1; j <= k; j ++)
        for(int i = 1; i + (1 << j) - 1 <= n; i ++)
            f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
//利用ST表查询区间[L,R]的最大值
int query(int L, int R) {
    int j = log2(R - L + 1);
    return max(f[L][j], f[R - (1 << j) + 1][j]);
}
int main()
{
    int m;
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) scanf("%d", a + i);;
    create();
    while(m --) {
        int L, R;
        scanf("%d%d", &L, &R);
        printf("%d\n", query(L, R));
    }
}

总结

RMQ（区间最值查询）问题有多种解决方法：

• ST表预处理的时间复杂度为$O(nlogn)$，查询时间复杂度为：$O(1)$，但是只能静态查询，不支持修改。
• 线段树处理的时间复杂度为$O(nlogn)$，查询时间复杂度为：$O(logn)$，支持实时修改。