🚀 算法题 🚀

🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样✨
🌲 作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯

🚀 算法题 🚀

🚗 知识回顾

大家在学习这道题目之前，可以先去看一下零钱兑换1，再看这个题目就更容易理解了。
博客的地址放到这里了，可以先去学习一下这到题目。

• 【LeetCode: 322. 零钱兑换 | 暴力递归=＞记忆化搜索=＞动态规划 | 背包模型】

🚩 题目链接

• 518. 零钱兑换 II

⛲ 题目描述

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。
示例 3：

输入：amount = 10, coins = [10]
输出：1

提示：

1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000

🌟 求解思路&实现代码&运行结果

---

⚡ 暴力法

🥦 求解思路

1. 我们来简单的概括一下题目的意思，题目要求我们可以从coins数组中进行选择，每一个硬币可以多次选择，凑成amount有多少方案数呢？
2. 比如此时我们从0到index(数组中某一个位置)位置一共凑齐了sum，sum小于amount，那么接下来我们该怎么办呢？我们是不是要从index位置继续开始，凑齐剩下值的方案数。所以我们使用递归来解决该问题。
3. 有了基本的思路，接下来我们就来通过代码来实现一下。

🥦 实现代码

class Solution {

    public int change(int amount, int[] coins) {
        return process(0,amount,coins);
    }

    public int process(int index,int amount,int[] coins){
        if(amount<0) return 0;
        if(amount==0) return 1;
        int sum=0;
        for(int i=index;i<coins.length;i++){
            sum+=process(i,amount-coins[i],coins);
        }
        return sum;
    }
}

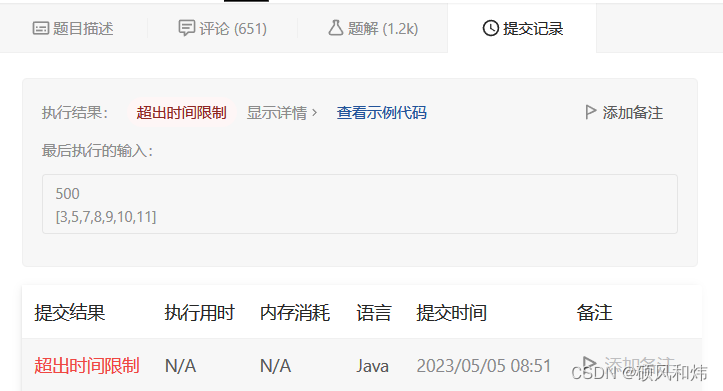
🥦 运行结果

时间超限了，不要紧张，我们来继续优化它！

---

⚡ 记忆化搜索

🥦 求解思路

1. 因为在递归的过程中，会重复的出现一些多次计算的结果，我们通过开辟一个数组，将结果提前缓存下来，算过的直接返回，避免重复计算，通过空间来去换我们的时间。

🥦 实现代码

class Solution {

    int[][] dp=new int[5050][5050];

    public int change(int amount, int[] coins) {
        for(int i=0;i<5050;i++){
            Arrays.fill(dp[i],-1);
        }
        return process(0,amount,coins);
    }

    public int process(int index,int amount,int[] coins){
        if(amount<0) return 0;
        if(amount==0){
            dp[index][amount]=1;
            return dp[index][amount];
        }
        if(dp[index][amount]!=-1) return dp[index][amount];
        int sum=0;
        for(int i=index;i<coins.length;i++){
            sum+=process(i,amount-coins[i],coins);
        }
        dp[index][amount]=sum;
        return dp[index][amount];
    }
}

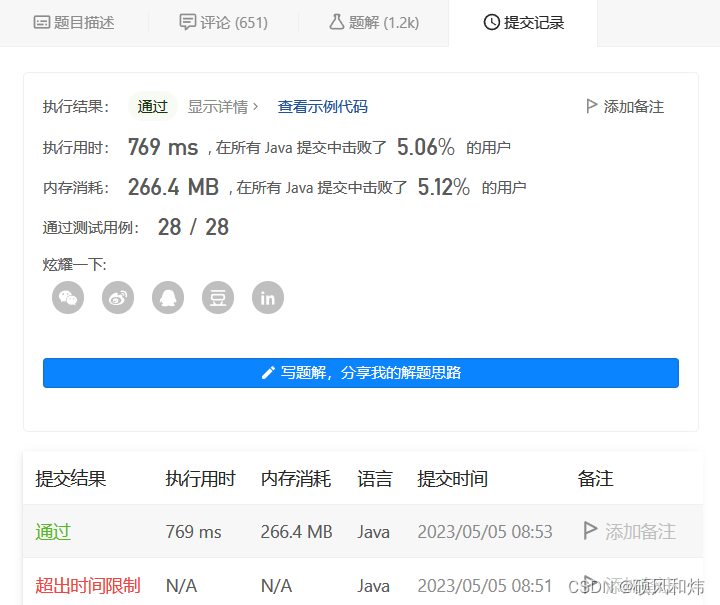
🥦 运行结果

我们发现，通过加一个缓存表，时间复杂度发生了翻天覆地的变化，真是不可思议！

---

⚡ 动态规划

🥦 求解思路

1. 有了递归，有了记忆化搜索，接下来就是动态规划了，直接上手。

🥦 实现代码

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp=new int[amount+1];
        dp[0]=1;
        for(int v:coins){
            for(int target=1;target<=amount;target++){
                if(target>=v){
                    dp[target]+=dp[target-v];
                }
            }
        }
        return dp[amount];
    }
}

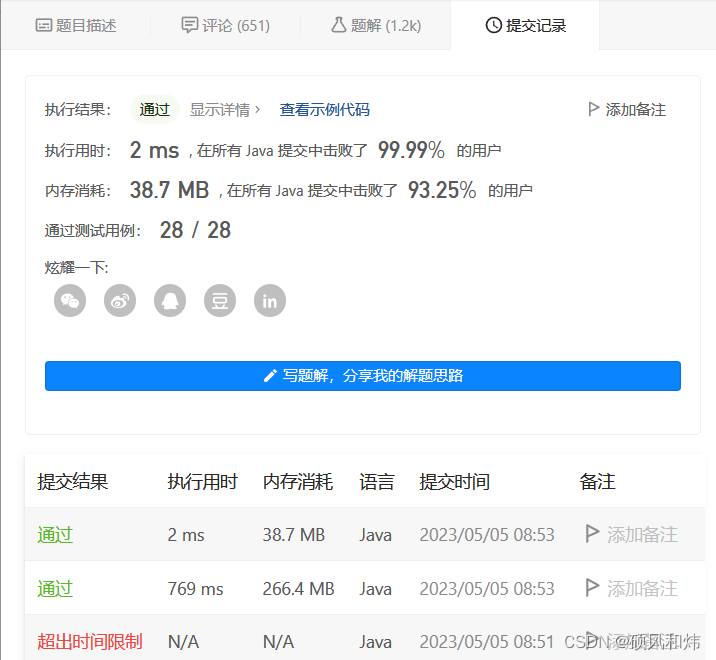
🥦 运行结果

---

💬 共勉

最后，我想和大家分享一句一直激励我的座右铭，希望可以与大家共勉！