引入
函数既可以嵌套定义也可以嵌套调用。嵌套定义指的是在定义一个函数时在该函数内部定义另一个函数;嵌套调用指的是在调用一个函数的过程中函数内部有调用另一个函数。而函数的递归调用指的是在调用一个函数的过程中又直接或者间接的调用该函数本身。
函数递归介绍
函数递归就是函数的递归调用,是函数嵌套调用的一种特殊形式,具体就是指在调用一个函数的过程中直接或者间接的调用到本身,递归的本质就是循环做重复的事情。
在调用func的过程中又调用func,这就是直接调用函数本身;
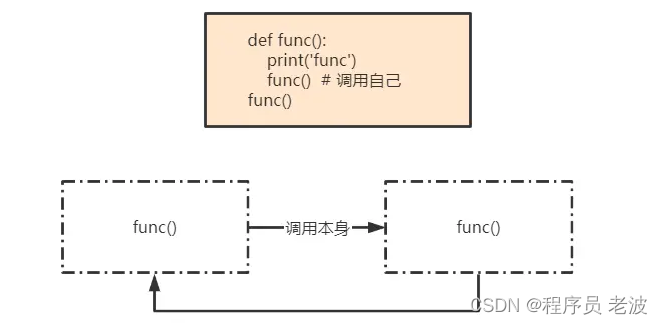
在调用func的过程中调用foo,而在调用foo的过程中又调用func,这就是间接调用func本身。
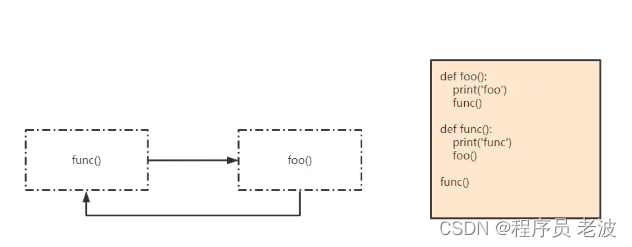
通过上面的分析,两种情况下的函数递归调用都是一个无限循环的过程,Python为了防止函数递归进入无限循环对函数递归调用的深度做了限制,一旦超出限制就会抛出异常。
def foo():
print('foo')
func()
def func():
print('func')
foo()
func()
'''
程序运行结果:
RecursionError: maximum recursion depth exceeded while calling a Python object(超过最大递归深度)
'''
因此为了避免函数递归调用报错,就必须在满足某中条件的情况下结束对函数的递归调用。
def foo(n):
if n == 1:
print('递归结束')
return
else:
foo(n-1)
foo(2)
函数递归原理及使用
通过一个简单的小学数学题说明递归的原理及使用。
小一比小二多一个苹果,小二比小三多一个苹果,小三比小四多一个苹果,小四有两个苹果,问小一有几个苹果?
这个题目非常简单,解答思路如下:
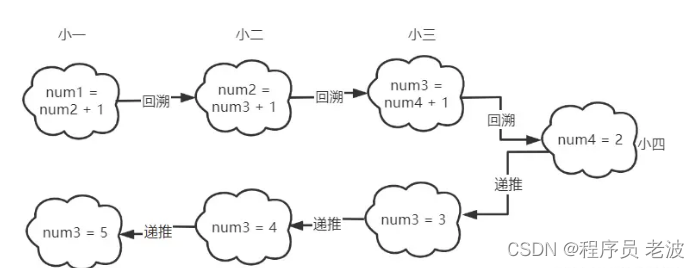
要想知道小一的苹果数量就需要知道小二的苹果数量,而小二的苹果数量又取决于小三,小三的苹果数量又是基于小四的苹果数量:
app_num(1) = app_num(2) + 1
app_num(2) = app_num(3) + 1
app_num(3) = app_num(4) + 1
app_num(4) = 2
因此可以总结出下面的结论:
app_num(4) = 2
app_num(x) = app_num(x+1) + 1
很明显是一个重复调用同一种方法的过程,只是参数不同,也就是一个递归的过程,通过上面的分析可以将递归过程分为两个阶段 - 回溯和递推。
回溯阶段:想要计算小一(x=1)的苹果数量就需要回溯得到小二(x+1)的苹果,以此类推,直到得到小四的苹果个数,此时app_num(4)已知,就无需再向前回溯。
递推阶段:从小四的苹果数量可以推算出小三的苹果数量,从小三的苹果数量可以推算出小二的,以此类推,一直推算出小一的苹果数量为止,递归结束。需要注意的是,递归一定要有结束条件,这里当x=1就是结束条件。
递归的本质就是在做重复的事情,理论上说递归可以解决的问题循环也都可以解决,只不过是在某种情况下使用递归更容易实现。
def apple_num(x):
if x == 4: # 结束递归的条件
return 2
return apple_num(x+1) + 1
apple_num1 = apple_num(1)
print(apple_num1) # 5
Practice
一个嵌套多层的列表要求打印出所有的元素。
list1 = [[[1, 2], [3, 4], [5, [6, 7], [8, 9, 10], 11, 12], 13]]
def func(items):
for elements in items:
if type(elements) is list:
func(elements)
else:
print(elements)
func(list1)
有一个按照从小到大顺序排列的数字列表,需要从该数字列表中找到我们想要的数字,如何更高效?
# 使用二分法:先取出列表的中间位置的值,与需要的数字进行比较,如果中间位置的值大于需要的值,那么就在中间值的左侧2 进行比较,如果小于,那么就在中间值的右侧进行比较,如果刚好等于,就输出值。然后对上述步骤进行循环
list1 = [0,2,5,7,9,11,34]
find_num = 2
def func(find_num,list1):
# 输出每次切分后生成的list1
print(list1)
mid_index = len(list1) // 2
if find_num > list1[mid_index]:
list1 = list1[mid_index+1:]
func(find_num,list1)
elif find_num < list1[mid_index]:
list1 = list1[:mid_index]
func(find_num,list1)
elif find_num == list1[mid_index]:
print(f'找到了{list1[mid_index]},索引为{mid_index}')
elif len(list1) == 0:
print('不存在这个值')
return
func(find_num,list1)