( 数组和矩阵) 766. 托普利茨矩阵 —

( 数组和矩阵) 766. 托普利茨矩阵 ——【Leetcode每日一题】

news2024/11/13 9:23:50

❓766. 托普利茨矩阵

难度：简单

给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵，返回 true ；否则，返回 false 。

如果矩阵上每一条由左上到右下的对角线上的元素都相同，那么这个矩阵是 托普利茨矩阵 。

示例 1：

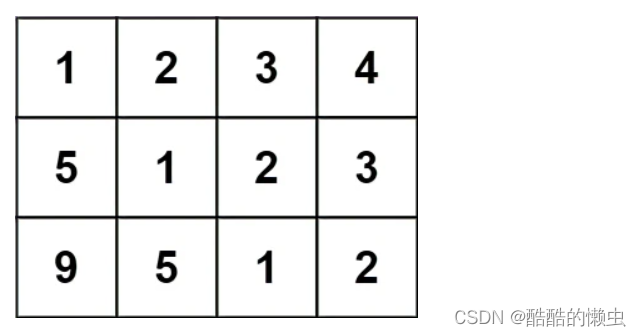
在这里插入图片描述

输入：matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
输出：true
解释：
在上述矩阵中, 其对角线为:
“[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”。
各条对角线上的所有元素均相同, 因此答案是 True 。

示例 2：

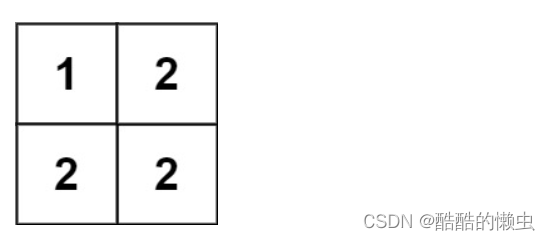
在这里插入图片描述

输入：matrix = [[1,2],[2,2]]
输出：false
解释：
对角线 “[1, 2]” 上的元素不同。

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 20
0 <= matrix[i][j] <= 99

进阶：

如果矩阵存储在磁盘上，并且内存有限，以至于一次最多只能将矩阵的一行加载到内存中，该怎么办？
如果矩阵太大，以至于一次只能将不完整的一行加载到内存中，该怎么办？

💡思路：

根据定义，当且仅当矩阵中每个元素都与其左上角相邻的元素（如果存在）相等时，该矩阵为托普利茨矩阵。

因此，我们遍历该矩阵，将每一个元素和它左上角的元素相比对即可。

进阶问题

问题1，一次最多只能将矩阵的一行加载到内存中：

我们将每一行复制到一个连续数组中，随后在读取下一行时，就与内存中此前保存的数组进行比较。

问题2，一次只能将不完整的一行加载到内存中：

我们将整个矩阵竖直切分成若干子矩阵，并保证两个相邻的矩阵至少有一列或一行是重合的，然后判断每个子矩阵是否符合要求。

🍁代码：(Java、C++)

Java

class Solution {
    public boolean isToeplitzMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] != matrix[i - 1][j - 1]) {
                    return false;
                }
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool isToeplitzMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] != matrix[i - 1][j - 1]) {
                    return false;
                }
            }
        }
        return true;
    }
};