0.引言

  因科研等多场景需要进行绘图处理，笔者对SPSS进行了学习，本文通过《SPSS统计分析从入门到精通》及其配套素材结合网上相关资料进行学习笔记总结，本文对回归分析进行阐述。

1.线性回归分析

  （1）准备数据
  

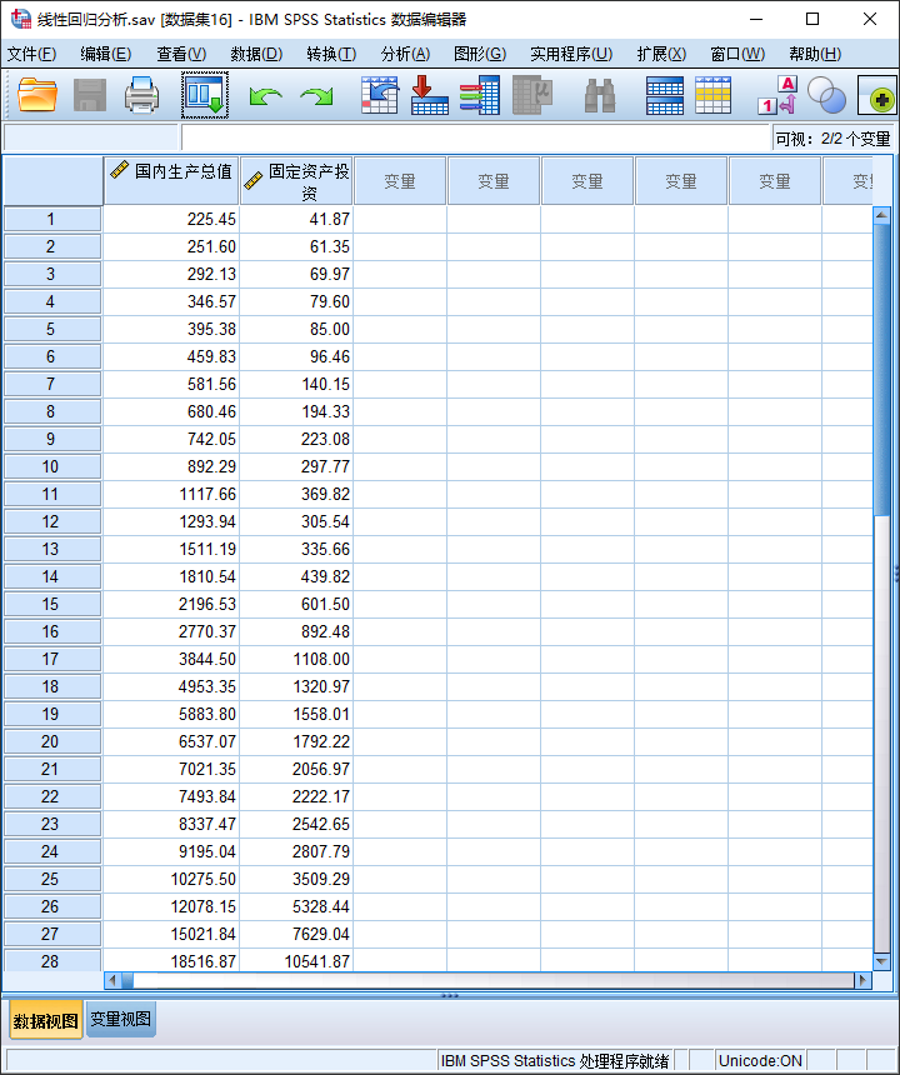
  （2）操作步骤
  ①在菜单栏中选择“分析|回归|线性”；
  ②将“GDP”选入“因变量”列表框中，将“FAI”选入“自变量”列表框中；
  ③单击“统计”，选中“估计值”“模型拟合”和“德宾-沃森”，单击“继续”；
  ④单击“图”，选中“直方图”和“正态概率图”，单击“继续”；
  ⑤单击“选项”，选中“在方程中包含常量“，单击”继续“；
  ⑥单击“确定”，执行线性回归分析。

  （3）操作结果
  ①查看输入/除去的变量
  

  ②查看模型摘要
  

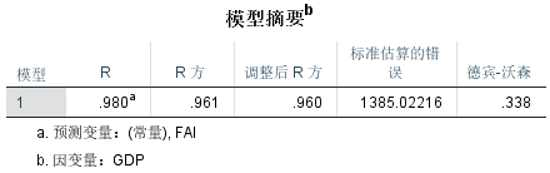
  ③查看ANOVA
  

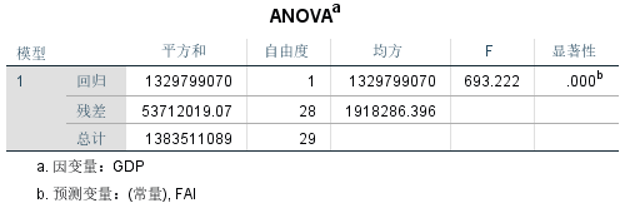
  ④查看系数
  

  ⑤查看残差统计
  

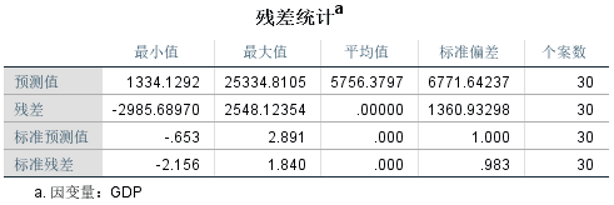
  ⑥查看直方图
  

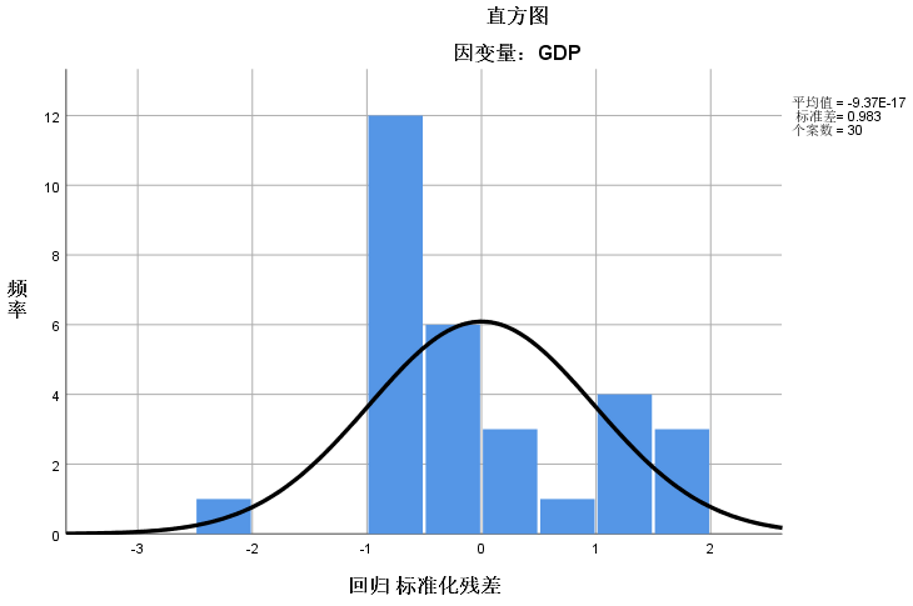
  ⑦查看正态概率图
  

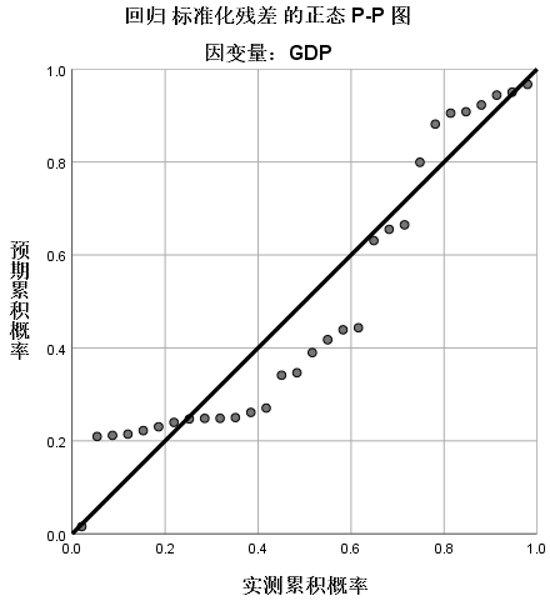
2.曲线回归分析

  （1）准备数据
  

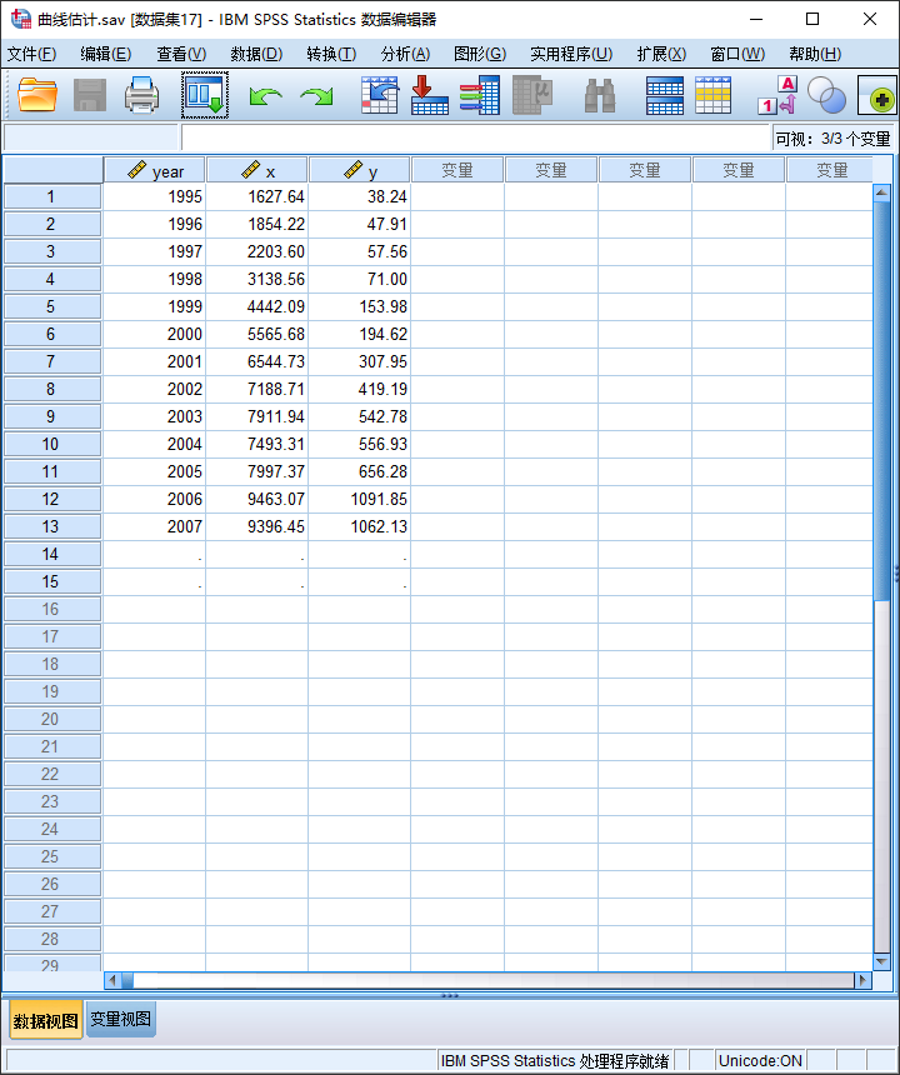
  （2）操作步骤
  ①在菜单栏中选择“分析|回归|曲线估算”；
  ②将Y选入“因变量”列表框中，将X选入“变量”列表框中；
  ③在“模型”中选中“线性”“对数”和“二次”，单击“继续”；
  ④单击“确定”，执行曲线回归分析。

  （3）操作结果
  ①查看模型描述
  

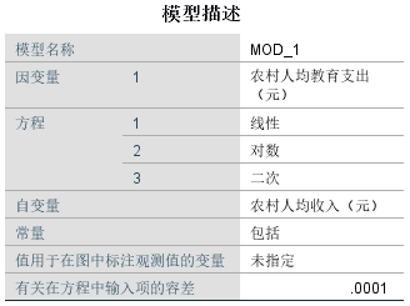
  ②查看个案处理摘要
  

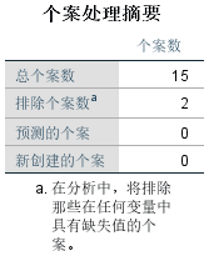
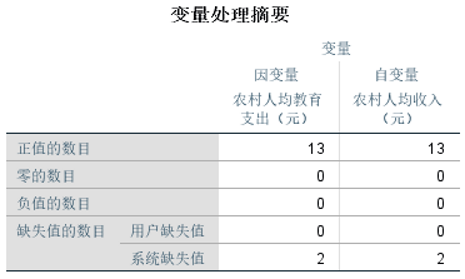
  ③查看变量处理摘要
  

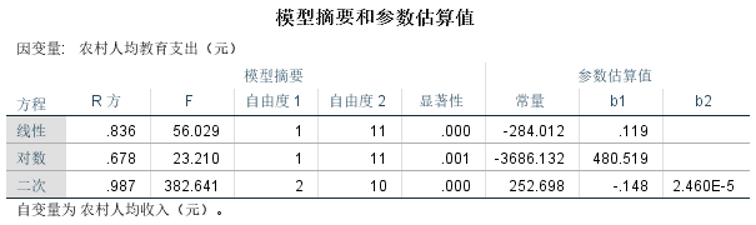
  ④查看模型摘要和参赛估算值
  

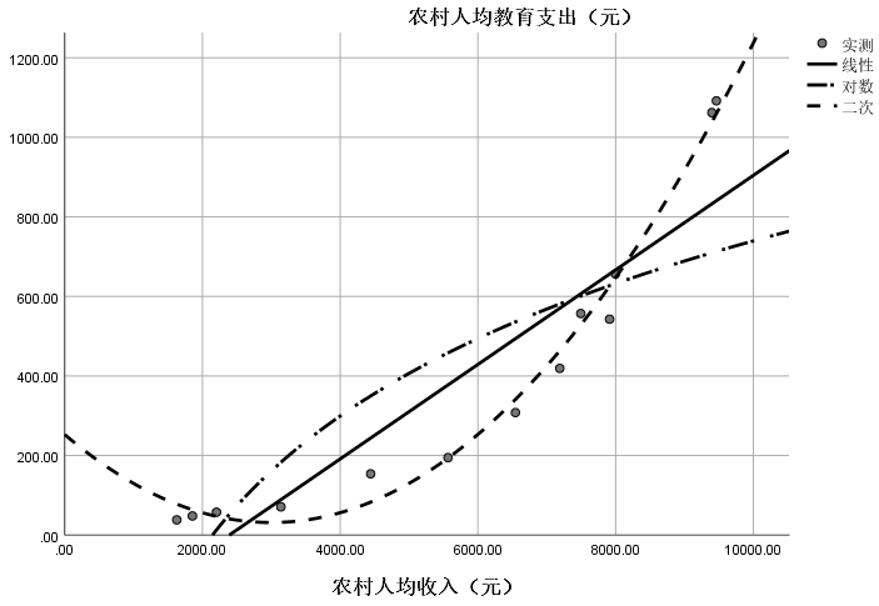
  ⑤查看农村人均教育支出
  

3.非线性回归分析

  （1）准备数据
  

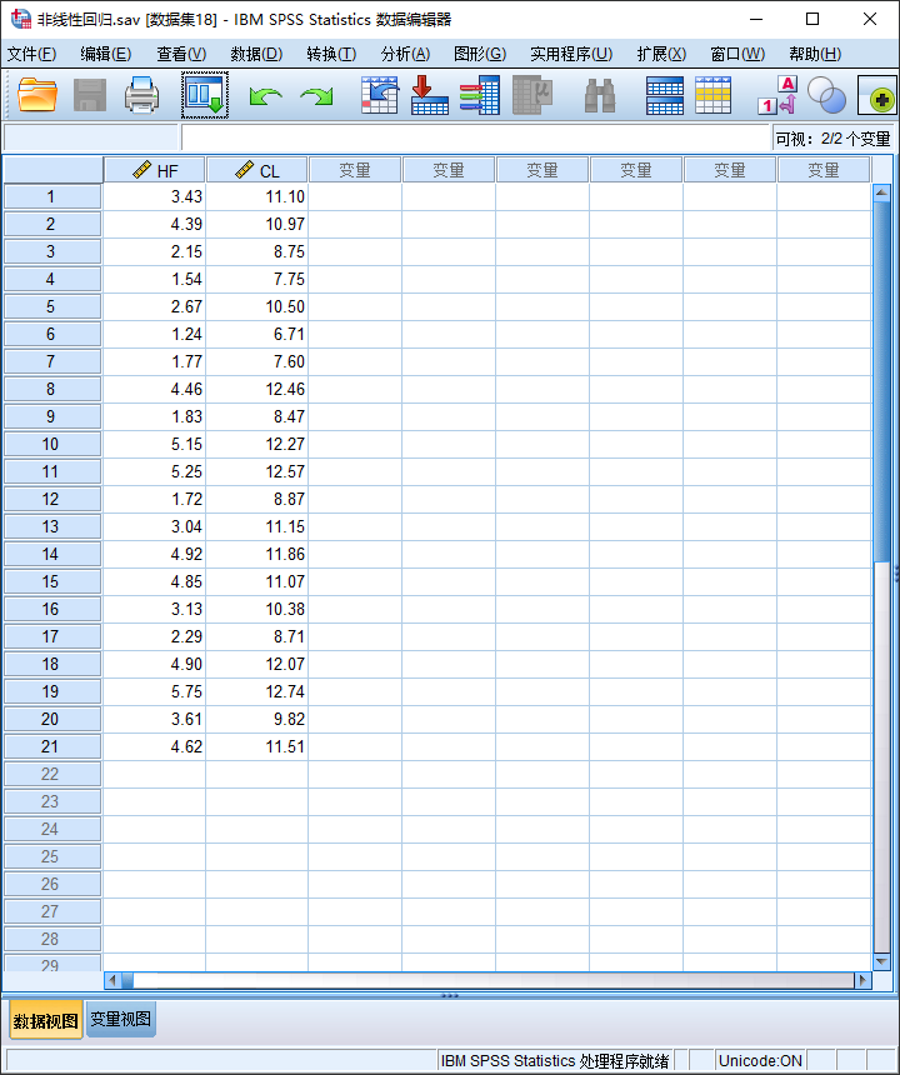
  （2）操作步骤
  ①在菜单栏中选择“分析|回归|非线性”；
  ②从源变量列表框中选择“CL”变量，将其选入“因变量”列表框中，设置模型表达式为a+bEXP(cHF)；
  ③单击“参数”，设置参数的开始值a=13、b=-6.5、c=-1.5（通过两变量的散点图看出）；
  ④单击保存，选中“残差”，单击“继续”；
  ⑤单击“确定”，执行非线性回归分析。

  （3）操作结果
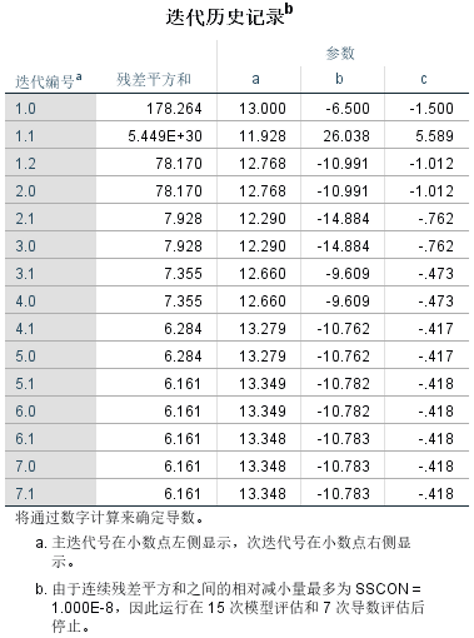
  ①查看迭代历史记录
  

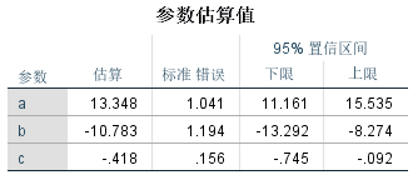
  ②参数估算值
  

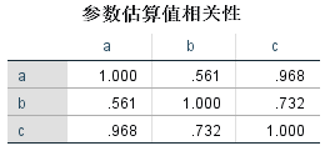
  ③查看参数估算相关性
  

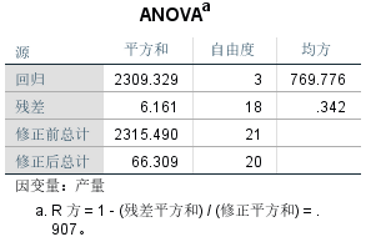
  ④查看ANOVA
  

4.Logistic回归分析

  （1）准备数据
  

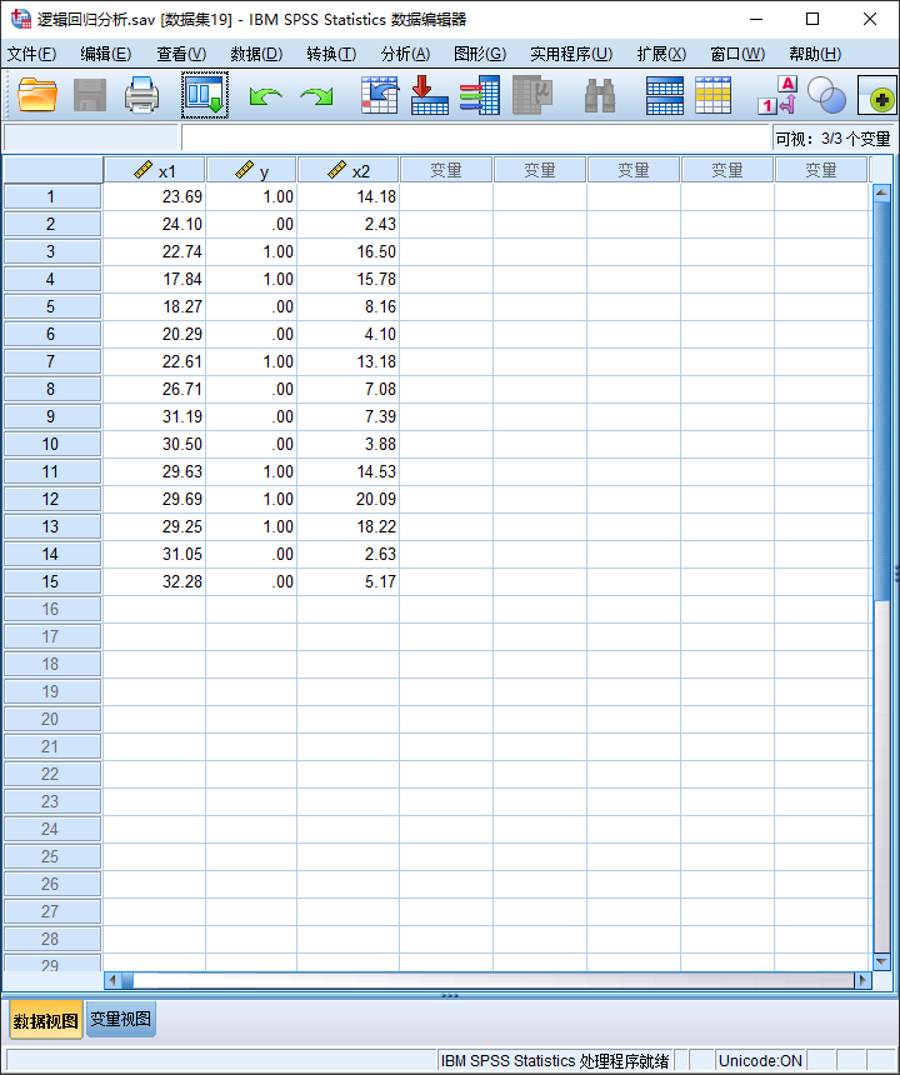
  （2）操作步骤
  ①在菜单栏中选择“分析|回归|二元Logistic”；
  ②将“y”选入“因变量”列表框中，将“x1”和“x2”选入“协变量”列表框中；
  ③单击“选项”，选中“分类图”，单击“继续”；
  ④单击“确定”，执行二元Logistic分析。

  （3）操作结果
  ①查看个案处理摘要
  

  ②查看因变量编码
  

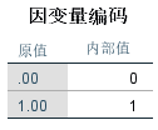
  ③查看块0：起始块
  

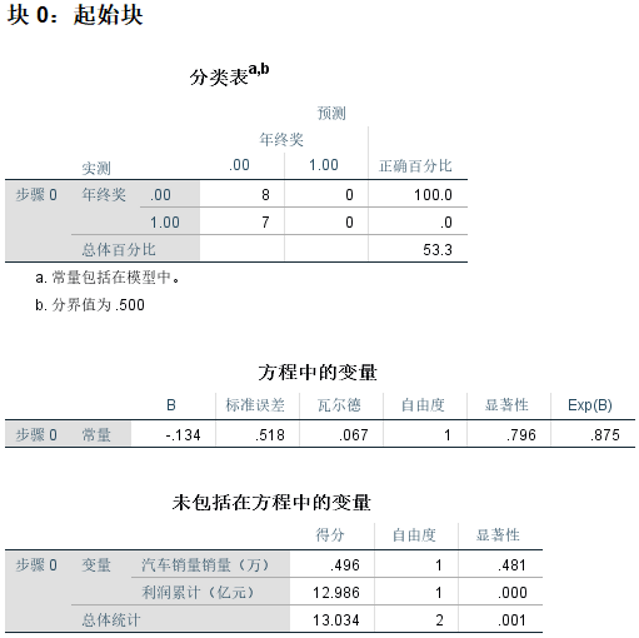
  ④查看块1：方法=输入
  

5.有序回归分析

  （1）准备数据
  

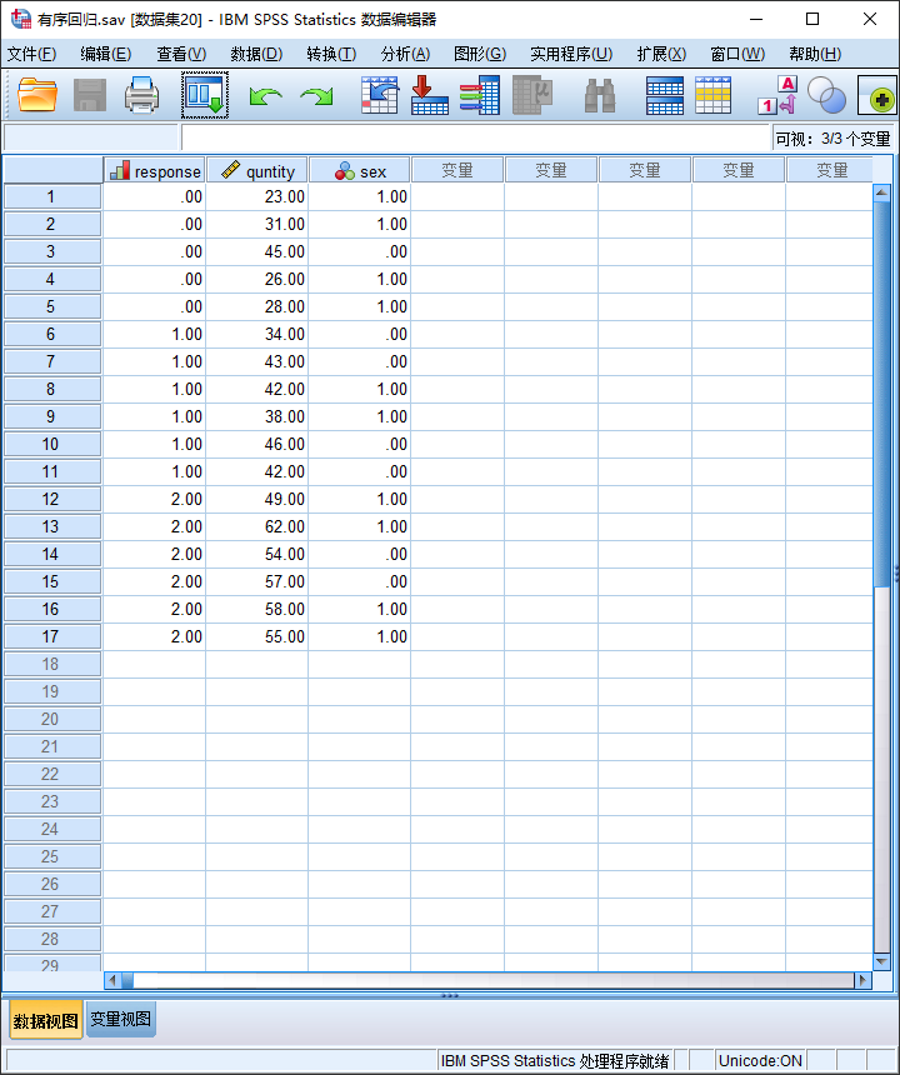
  （2）操作步骤
  ①在菜单栏中选择“分析|回归|有序”；
  ②将“response”选入“因变量”列表框中，将“quntity”选入“因子”列表框中，将“sex”选入“协变量”列表框中；
  ③单击“确定”，执行有序回归分析。

  （3）操作结果
  ①查看个案处理摘要
  

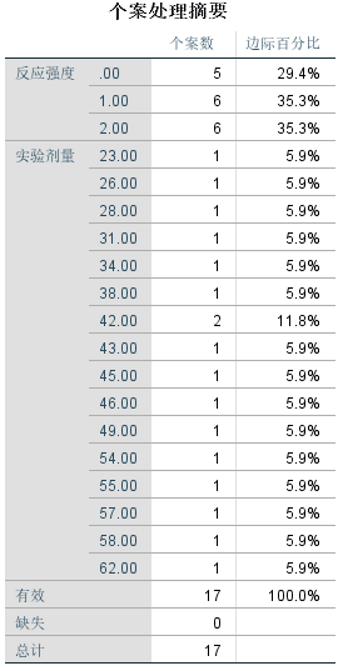
  ②查看模型拟合信息
  

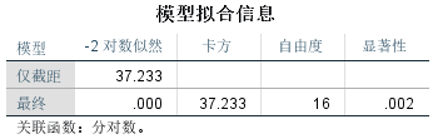
  ③查看拟合优度
  

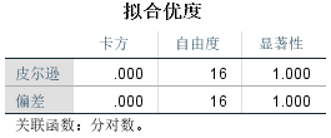
  ④查看伪R方
  

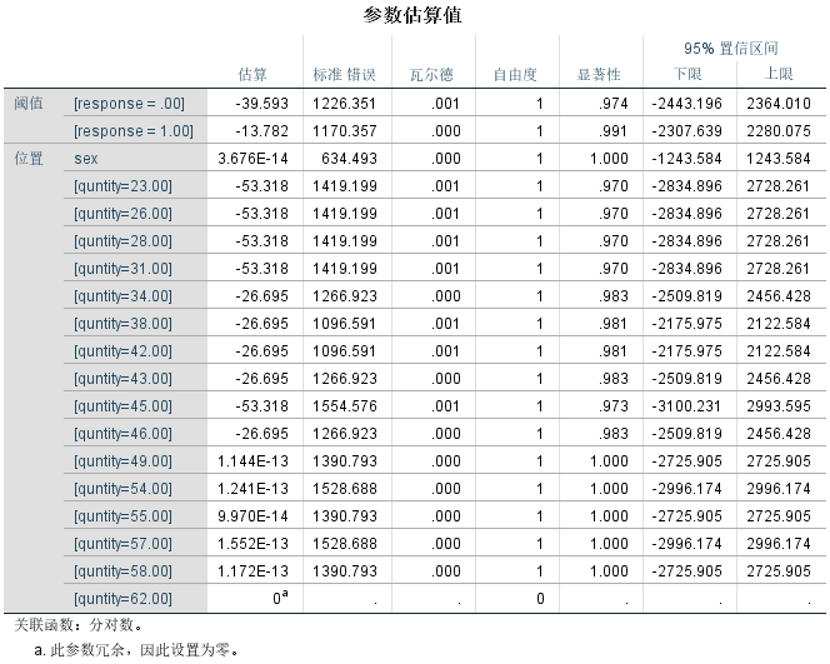
  ⑤查看参数估算值
  

6.概率回归分析

  （1）准备数据
  

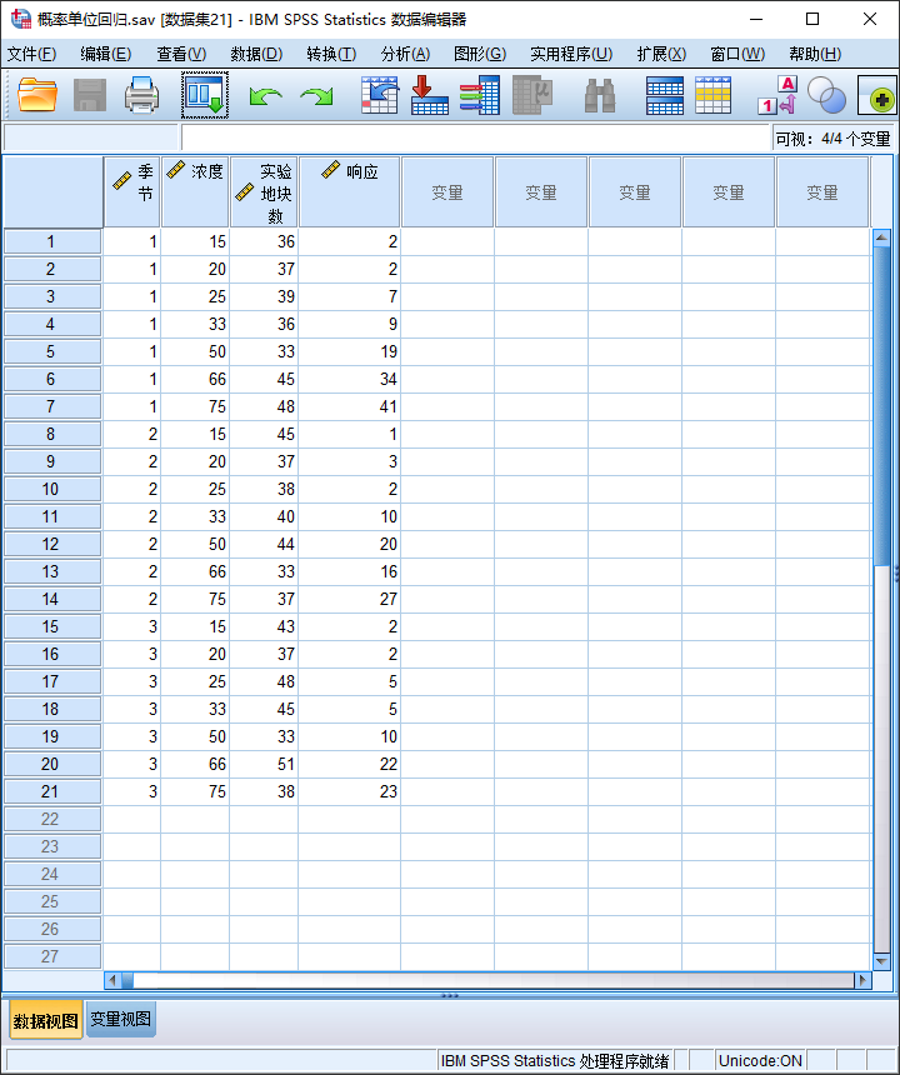
  （2）操作步骤
  ①在菜单栏中选择“分析|回归|概率”；
  ②将“响应“变量选入”响应频率“列表框中、将“季节”选入“因子”列表框中，将“实验地块数”选入“实测值总数”列表框汇总，将“浓度”选入“协变量”列表框中，然后单击“定义范围”，将“最小值”文本框输入1，在“最大值”文本框输入3，在“转换”下拉列表框中选择“自然对数”选项；
  ③单击“选项”，选中“平行检验”和“根据数据计算”，单击“继续”；
  ④单击“确定”，执行概率回归分析。

  （3）操作结果
  

7.加权回归分析

  （1）准备数据
  

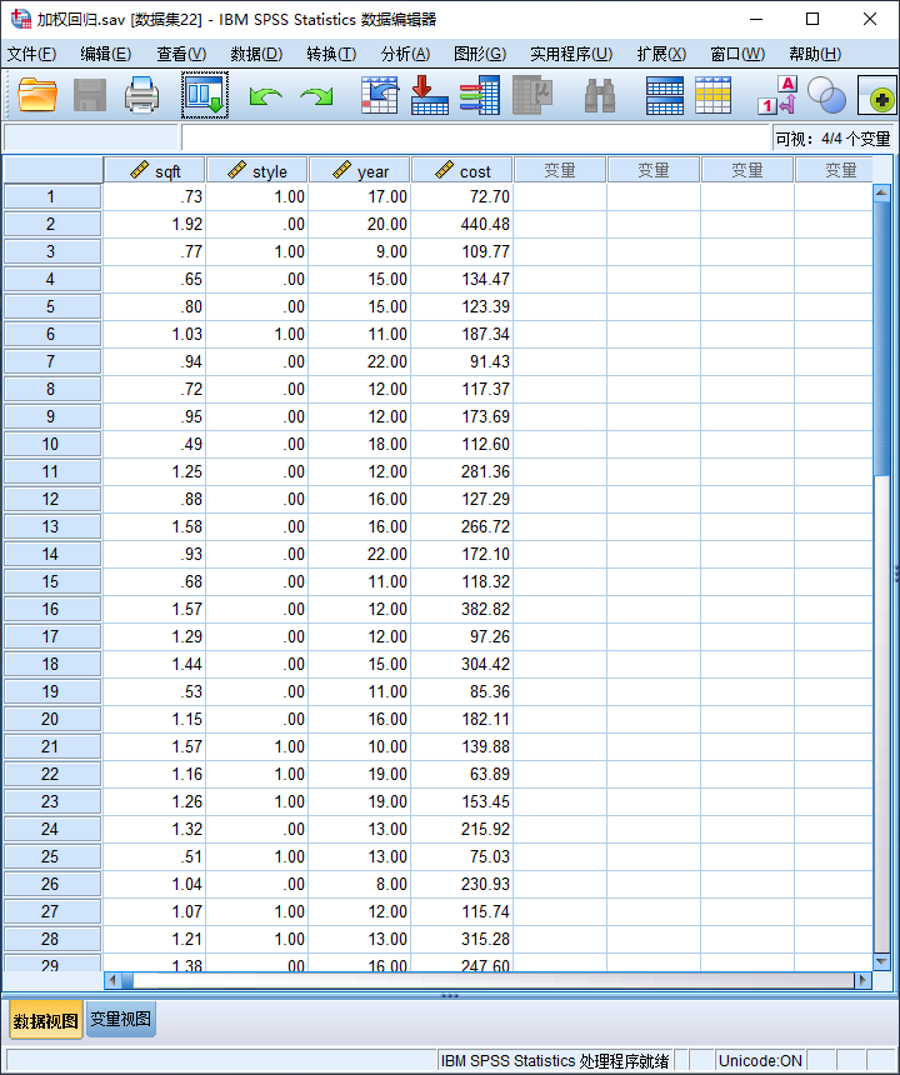
  （2）操作步骤
  ①在菜单栏中选择“分析|回归|权重估算”；
  ②从源变量列表框中选择“sqft”“style”和“year”变量，将其选入“自变量”列表框中，从源变量列表框中选择“cost”变量，将其置入“因变量”列表框中；
  ③从源变量列表框中选择“sqft”变量，将其置入“权重变量”列表框中，在“幂的范围”文本框中输入加权指数的初始值与结束值2和5，在“按”文本框中输入加权指数的步长0.5；
  ④单击“确定”，执行权重估算回归分析。

  （3）操作结果
  

参考资料：
[1] 机电工程有志青年. spss教程：线性回归分析; 2013-11-20 [accessed 2023-05-04].
[2] adminms. 用SPSS进行曲线回归分析实例; 2010-12-18 [accessed 2023-05-04].
[3] weixin_39988476. spss非线性回归分析步骤_SPSS篇—回归分析; 2020-11-21 [accessed 2023-05-04].
[4] Xkd_tianshi. spss二分类的logistic回归的操作和分析方法; 2018-03-25 [accessed 2023-05-04].
[5] 数据小兵. 用SPSS做有序多分类logistic回归分析; 2019-11-06 [accessed 2023-05-04].
[6] 侠胆医心. 有序回归的SPSS分析与解释; 2017-05-30 [accessed 2023-05-04].
[7] IBM SPSS. 怎样使用SPSS的概率回归方法分析数据; 2021-04-27 [accessed 2023-05-04].
[8] PY_smallH. SPSS----加权回归分析你了解多少（随笔笔记）; 2021-10-15 [accessed 2023-05-04].