LC-2106. 摘水果（滑动窗口）

2106. 摘水果

难度困难78

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作一步。你总共可以走最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

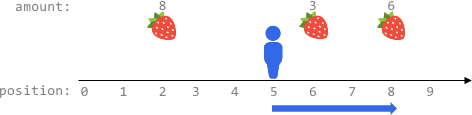
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：
- 向右移动到位置 6 ，摘到 3 个水果
- 向右移动到位置 8 ，摘到 6 个水果
移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

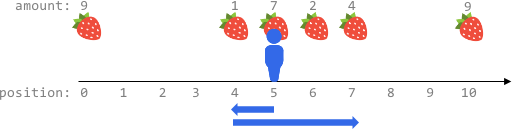
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：
- 在初始位置 5 ，摘到 7 个水果
- 向左移动到位置 4 ，摘到 1 个水果
- 向右移动到位置 6 ，摘到 2 个水果
- 向右移动到位置 7 ，摘到 4 个水果
移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

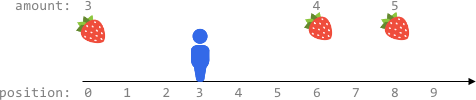
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：

1 <= fruits.length <= 105
fruits[i].length == 2
0 <= startPos, positioni <= 2 * 105
对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0 开始计数）
1 <= amounti <= 104
0 <= k <= 2 * 105

滑动窗口

题解：https://leetcode.cn/problems/maximum-fruits-harvested-after-at-most-k-steps/solution/hua-dong-chuang-kou-jian-ji-xie-fa-pytho-1c2d/

设向左走最远可以到达 fruts[left][0] ，这可以用枚举或者二分查找得出，其中 left 是最小的满足fruits[left][0] > startPos - k的下标，

假设位置不超过 startPos 的最近水果在 fruits[right][0]，那么当 right 增加时，left 不可能减少，有单调性，因此可以用同向双指针（滑动窗口）解决。

如何判断 left 是否需要增加呢?

如果先向右再向左，那么移动距离为(fruits[right][0] - startPos) + (fruits[right][0] - fruits[left][0])

如果先向左再向右，那么移动距离为
(startPos - fruits[right][0]) + (fruits[right][0] - fruits[left][0])

如果上面两个式子均大于k，就说明 fruits[left][0] 太远了，需要增加left.

对于 right，它必须小于n，且满足fruits[right][0] <= startPos + k
移动 left 和 right 的同时，维护窗内的水果数量 s，同时用 s 更新答案的最大值

class Solution:
    # 区间和问题如果不是其中有负数，则优先用滑窗解决！！！
    def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:
        left = bisect_left(fruits, [startPos - k]) # 向左最远能到 fruits[left][0]
        right = bisect_left(fruits, [startPos + 1]) # startPos 右边最近水果（因为下面求的是左闭右开区间）

        ans = s = sum(c for _, c in fruits[left: right]) # 从 fruits[left][0] 到 startPos 的水果数
        while right < len(fruits) and fruits[right][0] <= startPos + k: 
            s += fruits[right][1] # 枚举最右位置为 fruits[right][0]
            while fruits[right][0] * 2 - fruits[left][0] - startPos > k and \
                  fruits[right][0] - fruits[left][0] * 2 + startPos > k:
                s -= fruits[left][1]  # fruits[left][0] 无法到达
                left += 1
            ans = max(ans, s)  # 更新答案最大值
            right += 1  # 继续枚举下一个最右位置
        return ans