题目:
给你一个下标从 0 开始的二维整数数组 nums 。
返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数,返回 0 。
注意:
- 如果某个整数大于
1,且不存在除1和自身之外的正整数因子,则认为该整数是一个质数。 - 如果存在整数
i,使得nums[i][i] = val或者nums[i][nums.length - i - 1]= val,则认为整数val位于nums的一条对角线上。
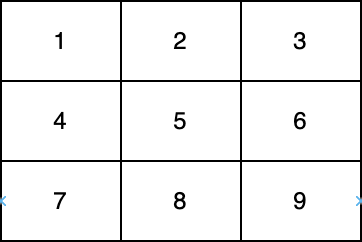
在上图中,一条对角线是 [1,5,9] ,而另一条对角线是 [3,5,7] 。
示例 1:
输入:nums = [[1,2,3],[5,6,7],[9,10,11]] 输出:11 解释:数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数,故返回 11 。
示例 2:
输入:nums = [[1,2,3],[5,17,7],[9,11,10]] 输出:17 解释:数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数,故返回 17 。
提示:
1 <= nums.length <= 300nums.length == numsi.length1 <= nums[i][j] <= 4*106
代码:
class Solution:
def diagonalPrime(self, nums: List[List[int]]) -> int:
num_list = []
# 寻找主对角线数据
for i in range(len(nums)):
num_list.append(nums[i][i])
num_list.append(nums[i][len(nums)-i-1])
# 对主对角线数据进行排序
num_list.sort()
print(num_list)
if num_list[len(num_list)-1] == 1:
return 0
for i in range(len(num_list)):
flag = True
number = num_list[len(num_list)-1-i]
for i in range(2, number):
if number % i == 0:
flag = False
break
if flag == True:
return number
return 0
这段代码定义了一个名为Solution的类,并在其中定义了一个名为diagonalPrime的方法。该方法接受一个二维列表nums作为输入,表示一个方阵。方法首先提取矩阵的对角线元素(包括主对角线和反对角线),并将它们存储在一个名为num_list的列表中。然后,它将num_list按升序排序。
接下来,该方法检查num_list中最大的元素是否为1。如果是,则返回0。
如果最大元素不是1,则该方法按相反的顺序迭代num_list,检查每个元素是否为质数。如果找到一个元素是质数,该方法返回该元素。如果在迭代完整个列表后没有找到质数,该方法返回0。
结果: