实验二主要使用隐式积分法以及PBD法完成布料仿真

完整项目已上传至github。

---

基于物理的方法

首先介绍一下弹簧系统

弹簧系统

单个弹簧

一个理想弹簧满足虎克定律：弹簧力尽力恢复原长，下面分别一端点为固定点(左图)和两端都不为固定点(右图)的能量$E(\vec{x})$与力关于位矢的函数$\vec{F}(\vec{x})$。对于两端点都不是固定点情况(这个系统受两个端点的位矢影响)， F ⃗ ( x ⃗ ) = { f i ⃗ ( x ⃗ ) , f j ⃗ ( x ⃗ ) } \vec{F}(\vec{x})=\{\vec{f_i}(\vec{x}),\vec{f_j}(\vec{x})\} F (x )={fi​ ​(x ),fj​ ​(x )}。这里的 x ⃗ = { x i ⃗ , x j ⃗ } \vec{x}=\{\vec{x_i},\vec{x_j}\} x ={xi​ ​,xj​ ​}。

多个弹簧

当有多个弹簧时，能量和力可以被简单累加(对于包含$\overrightarrow{x_i}$的系统)，注意不同的系统不是直接累加的。对于$x_i$的力$\overrightarrow{f_i}$可以通过能量$E$对位矢$\overrightarrow{x_i}$求梯度再取负数就能得到。

弹簧网络

结构化弹簧网络(Structured Spring Networks)

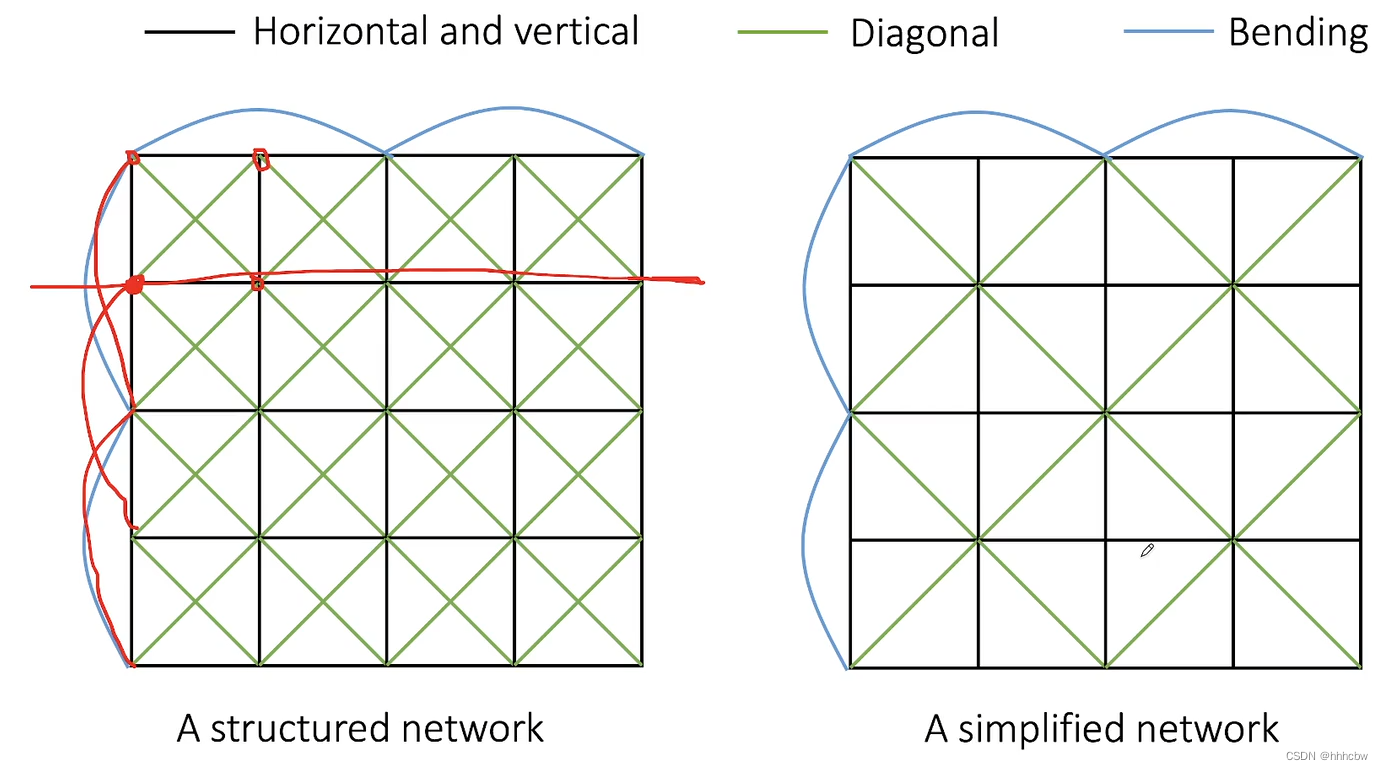
我们在横向与纵向(Horizontal and vertical)添加弹簧可以抵抗横向与纵向的拉伸(streching)。在对角增加弹簧可以抵抗在对角(diagonal)方向上的皱褶(实际应用中可以简化为只在一个小格子的其中一个对角线上添加弹簧)。跳过一个顶点连接的弹簧，抵抗沿中间的长边产生大的翻折(Bending)。

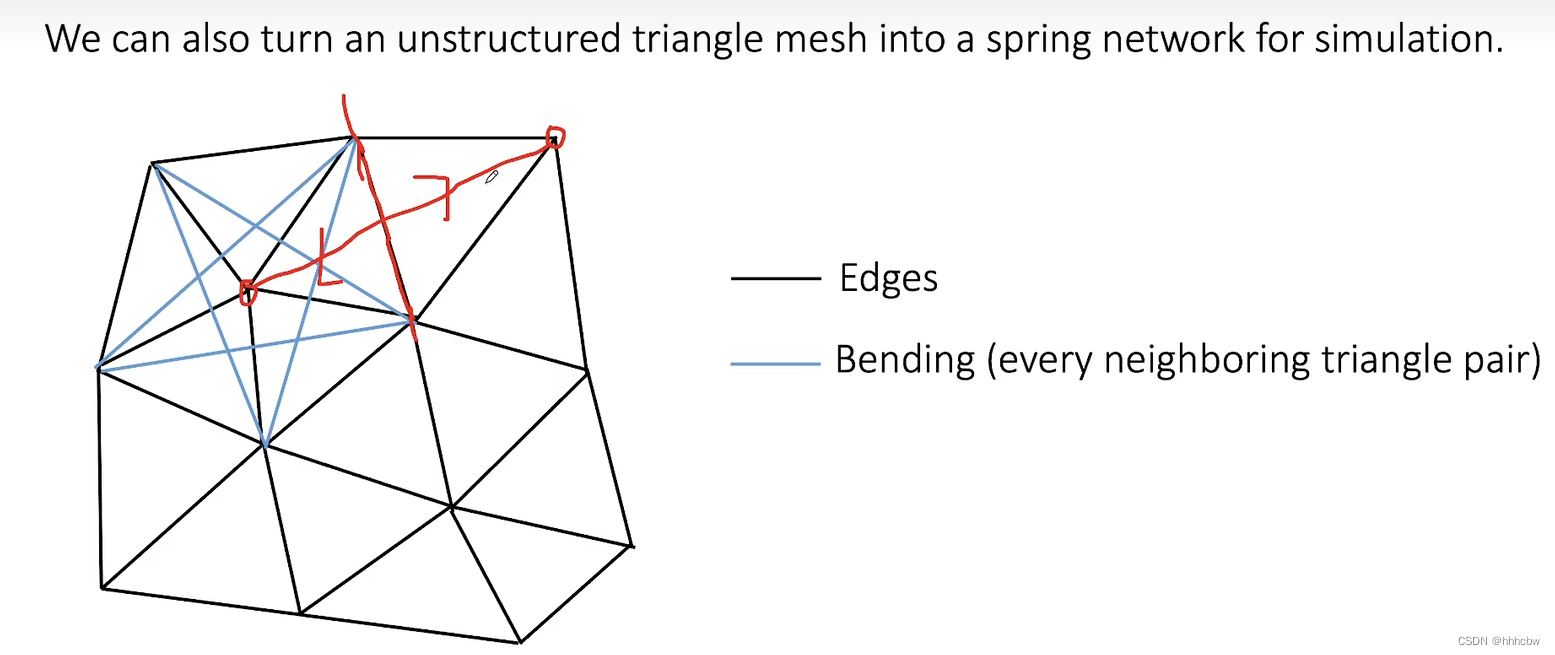
非结构化弹簧网络(Unstructured Spring Networks)

对于不规则形状的三角形 Mesh 布料，同样在三角网格的每个边上都加一根弹簧，然后跨过所有内部边添加弹簧(称任意两个相邻三角形的公共边为内部边，两个相邻三角形组成一个四边形，新添加的弹簧为这个四边形的对角线)来抵抗弯曲。

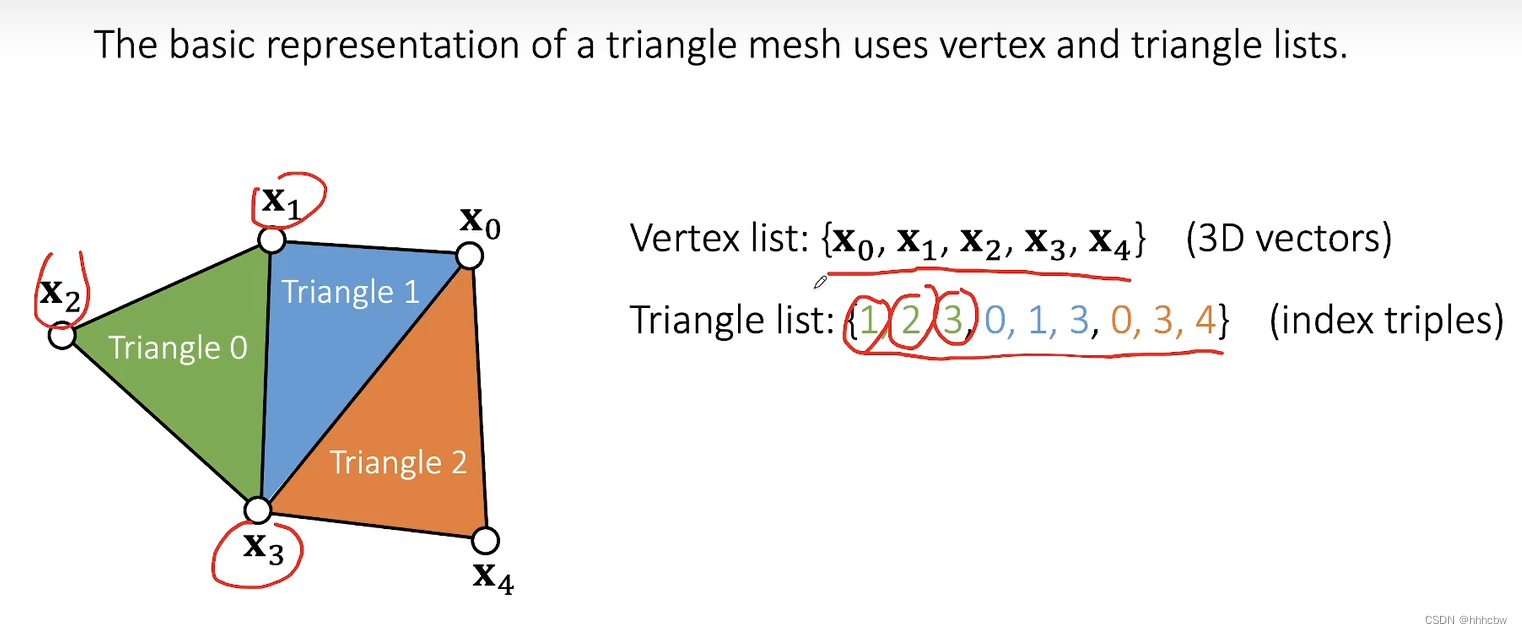
三角网格表示

基础的三角形网格使用表示使用顶点和三角形列表，顶点列表存放顶点位置，三角形列表存放每个三角形三个顶点在顶点列表的索引。

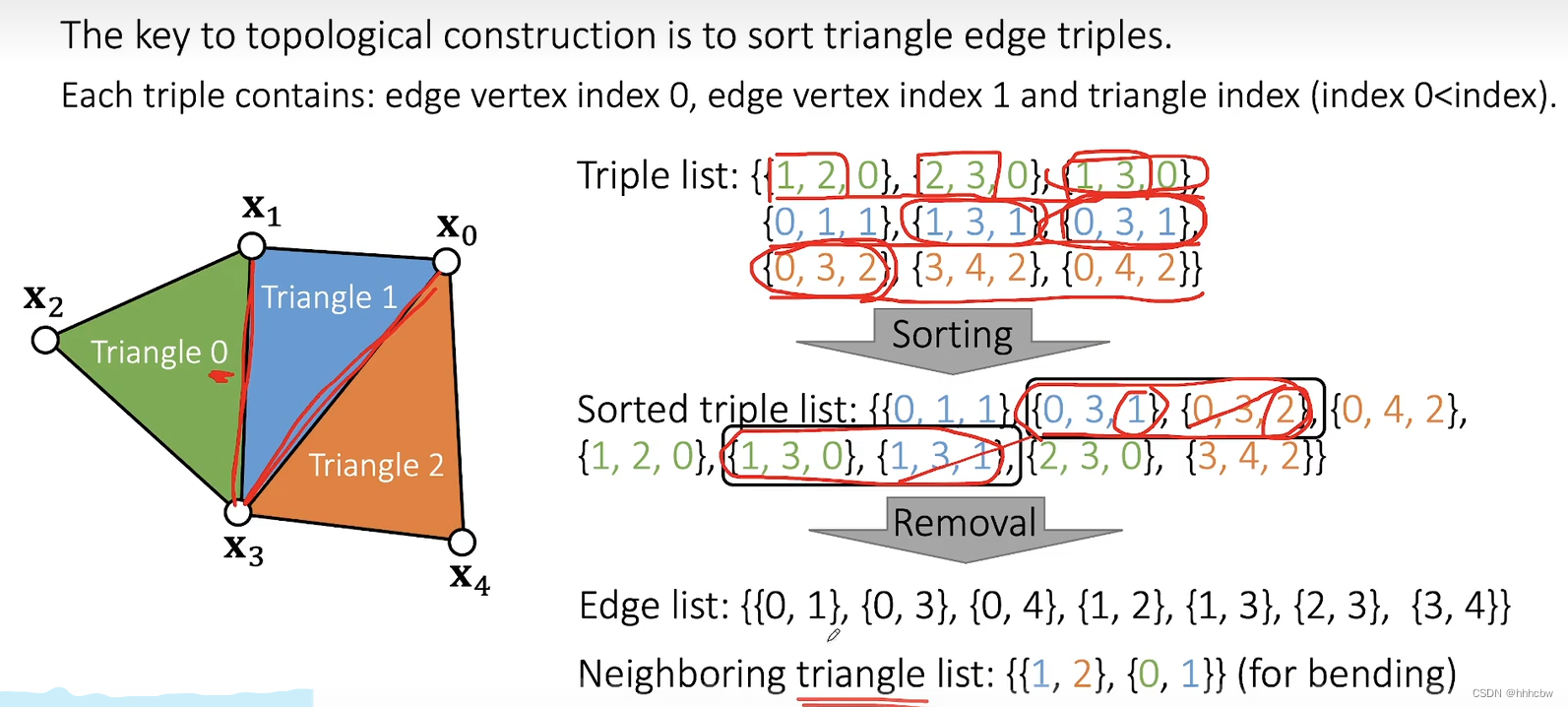
但如果只存储这些信息，我们在计算每条边的对应弹簧系统的力与能量会把内部边重复计算。因此还需要构建一个三元组的列表，其中每个三元组的三个元素分别为边两个顶点的索引及三角形的索引。然后进行一次排序(按两个顶点索引大小，以小的顶点为主序)，这样我们就可以找到所有内部边，将重复的剔除，得到最后的边列表。再计算相邻三角形对，就可以在之后用于bending的计算了。

代码

上述内容，在实验中的代码如下(没考虑bending)，这里网格的大小为 21x21，X[] 存放网格中每个顶点的位置，UV[] 存放每个顶点在纹理中的位置，triangles[] 存放每个三角形对应顶点的索引(在X[]的索引)，_E[] 存放每条边中的顶点的索引(此时还未去除重复边)。我们对 _E[] 排序去除重复边得到 E[]，L[] 为每根弹簧的原长。

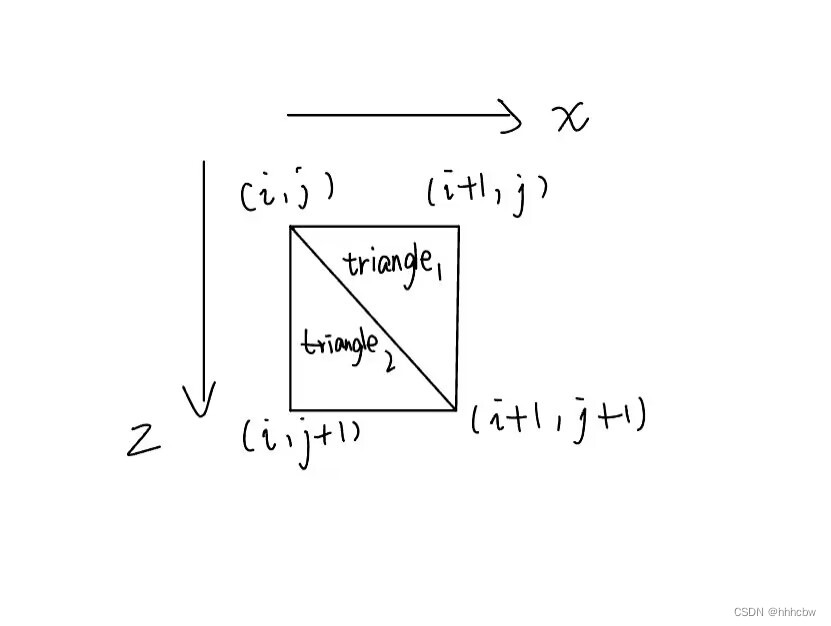
		Mesh mesh = GetComponent<MeshFilter>().mesh;

        //Resize the mesh.
        int n = 21;
        Vector3[] X = new Vector3[n * n];
        Vector2[] UV = new Vector2[n * n];
        int[] triangles = new int[(n - 1) * (n - 1) * 6];
        for (int j = 0; j < n; j++)
            for (int i = 0; i < n; i++)
            {
                X[j * n + i] = new Vector3(5 - 10.0f * i / (n - 1), 0, 5 - 10.0f * j / (n - 1));
                UV[j * n + i] = new Vector3(i / (n - 1.0f), j / (n - 1.0f));
            }
        int t = 0;
        for (int j = 0; j < n - 1; j++)
            for (int i = 0; i < n - 1; i++)
            {
                triangles[t * 6 + 0] = j * n + i;
                triangles[t * 6 + 1] = j * n + i + 1;
                triangles[t * 6 + 2] = (j + 1) * n + i + 1;
                triangles[t * 6 + 3] = j * n + i;
                triangles[t * 6 + 4] = (j + 1) * n + i + 1;
                triangles[t * 6 + 5] = (j + 1) * n + i;
                t++;
            }
        mesh.vertices = X;
        mesh.triangles = triangles;
        mesh.uv = UV;
        mesh.RecalculateNormals();

        //Construct the original E
        int[] _E = new int[triangles.Length * 2];
        for (int i = 0; i < triangles.Length; i += 3)
        {
            _E[i * 2 + 0] = triangles[i + 0];
            _E[i * 2 + 1] = triangles[i + 1];
            _E[i * 2 + 2] = triangles[i + 1];
            _E[i * 2 + 3] = triangles[i + 2];
            _E[i * 2 + 4] = triangles[i + 2];
            _E[i * 2 + 5] = triangles[i + 0];
        }
        //Reorder the original edge list
        for (int i = 0; i < _E.Length; i += 2)
            if (_E[i] > _E[i + 1])
                Swap(ref _E[i], ref _E[i + 1]);
        //Sort the original edge list using quicksort
        Quick_Sort(ref _E, 0, _E.Length / 2 - 1);

        int e_number = 0;
        for (int i = 0; i < _E.Length; i += 2)
            if (i == 0 || _E[i + 0] != _E[i - 2] || _E[i + 1] != _E[i - 1])
                e_number++;

        E = new int[e_number * 2];
        for (int i = 0, e = 0; i < _E.Length; i += 2)
            if (i == 0 || _E[i + 0] != _E[i - 2] || _E[i + 1] != _E[i - 1])
            {
                E[e * 2 + 0] = _E[i + 0];
                E[e * 2 + 1] = _E[i + 1];
                e++;
            }

        L = new float[E.Length / 2];
        for (int e = 0; e < E.Length / 2; e++)
        {
            int v0 = E[e * 2 + 0];
            int v1 = E[e * 2 + 1];
            L[e] = (X[v0] - X[v1]).magnitude;
        }

---

求解质量弹簧系统的显示积分法

在对隐式积分法进行说明之前，也介绍下显示积分法。显示积分法就是对当前状态计算出力，然后更新每个顶点的速度与位置。

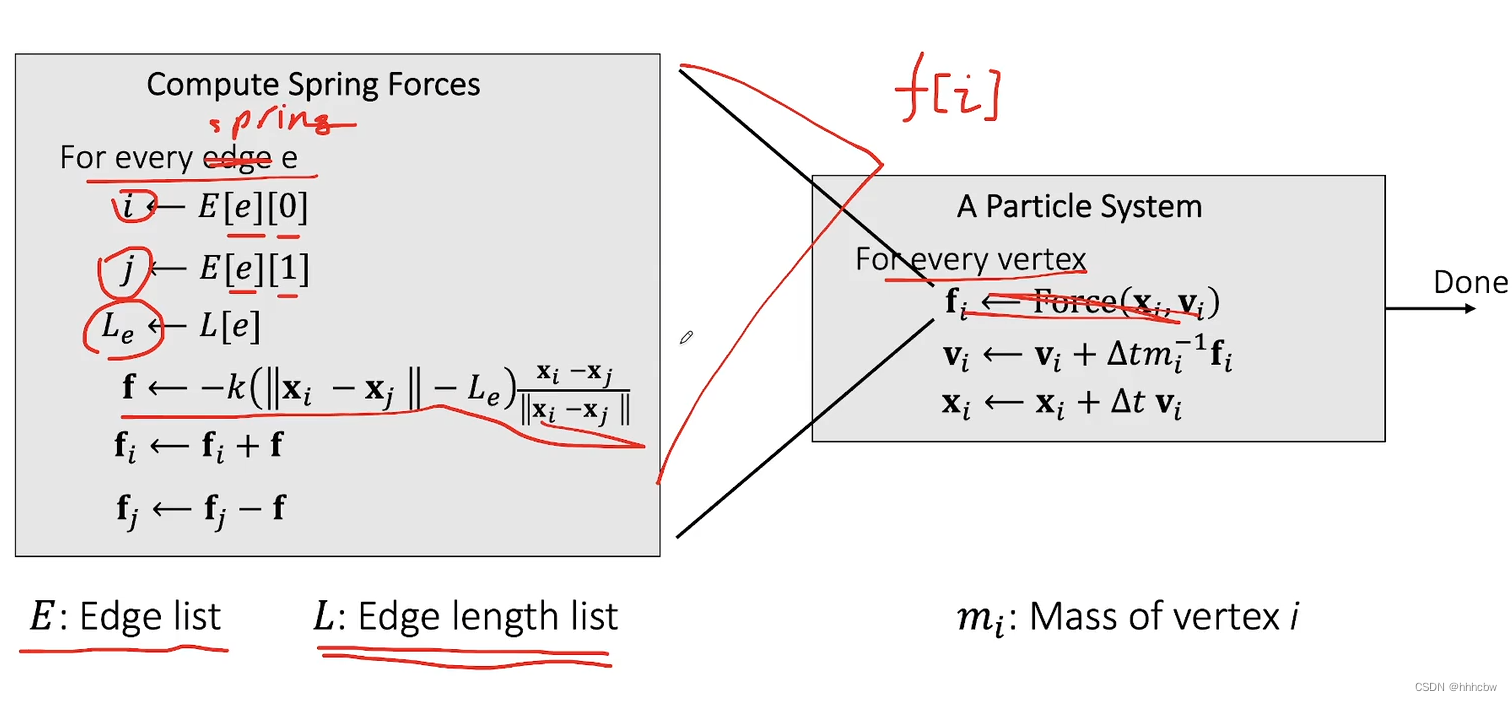
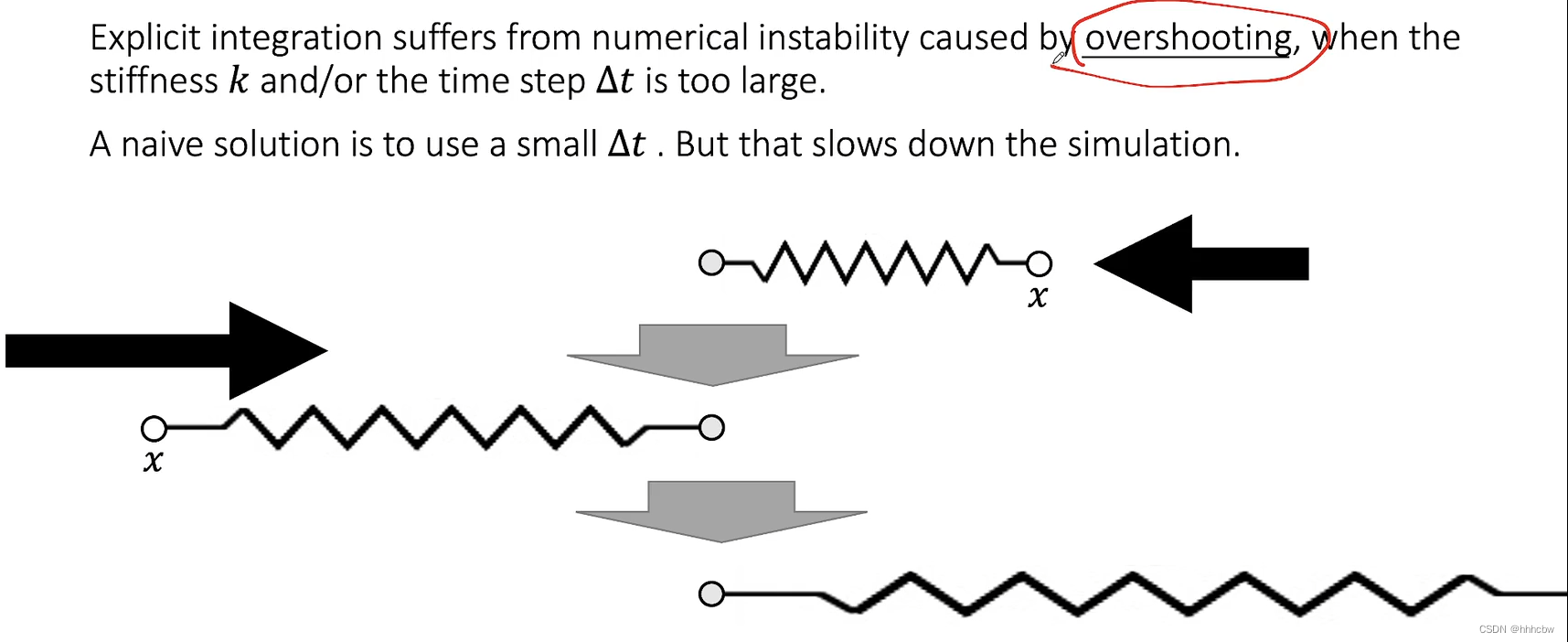
而使用隐式积分会因为overshooting导致数值不稳定， 因为$△t$不是无穷小，所以产生了莫名的能量；真实世界中当弹簧形变量缩小时弹力会逐渐减小，而离散的积分方法假定了一个时间步内受力都相同。当时间步长太大，或者弹性系数 k 太大时就会在一个时间步内产生过度的位移。

---

隐式积分法

显式积分是数值不稳定的，因此考虑使用隐式积分法。隐式积分法更新速度时用的是新的位置受到的力，也就是说当弹簧缩小时，显式积分用的弹力一定大于这个时间步内的平均弹力，而隐式积分用的力小于一个时间步内的平均弹力，因此隐式积分法在数值上更稳定一些。如果力只与端点的位置有关，那么$\vec{f}$只依赖$\overrightarrow{x^{[1]}}$。

我们对上面的等式进行转化，将其等价于求解一个优化问题

牛顿法

我们要求解优化问题 $x^{[1]}=argmin\vec{F}(\vec{x})$。就是寻找一个 ${\vec{F}}^{\prime }(\vec{x})=0$ 的点 $\vec{x}$，我们将 $\overrightarrow{F^{\prime }}(\vec{x})$ 使用泰勒展开，保留前两项，之后就可以转化为求解线性方程组的问题，使用求线性方程组解的方法即可。

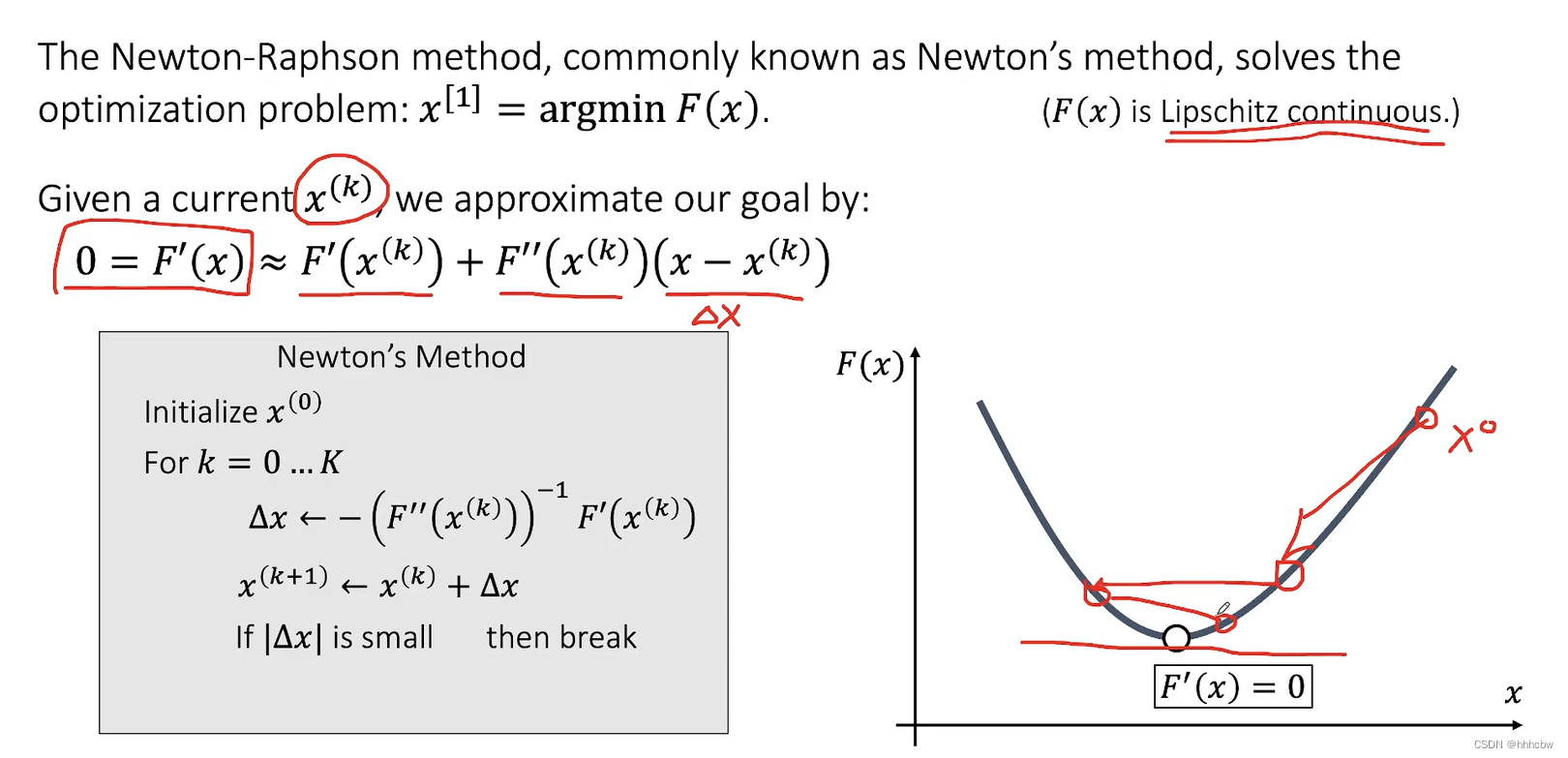
当然，$\overrightarrow{F^{\prime }}(\vec{x})=0$ 的点也可能是极大值点，因此需要二阶导判断。当然，如果这个函数的二阶导恒大于0，那么此时肯定是极小值点。

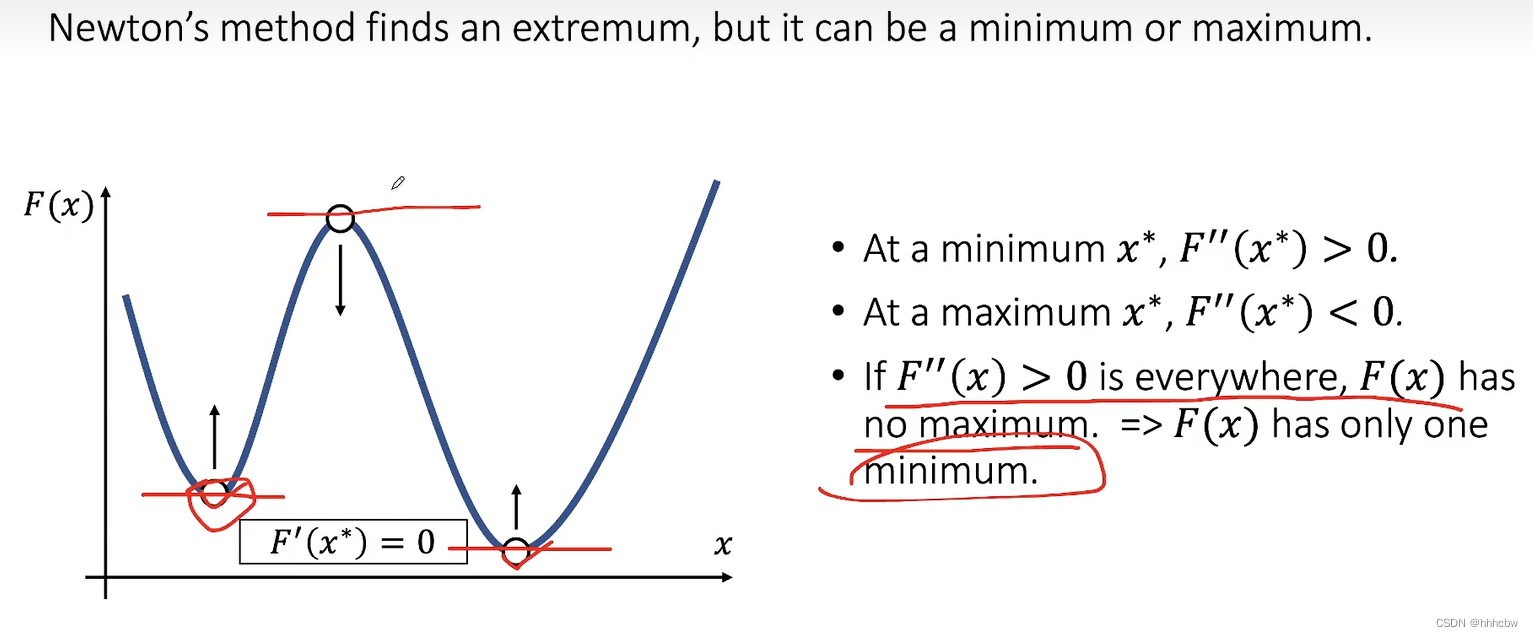
使用牛顿法的仿真过程

需要特别说明这里的海森矩阵，当海森矩阵对称正定，A(左边的矩阵)就正定，就一定能收敛(这也是作业中为什么可以使用一个魔法矩阵来代替的原因)，这里的海森矩阵，当弹簧是拉伸的时候，就一定是对称正定的。如果是压缩，则不一定对称正定。


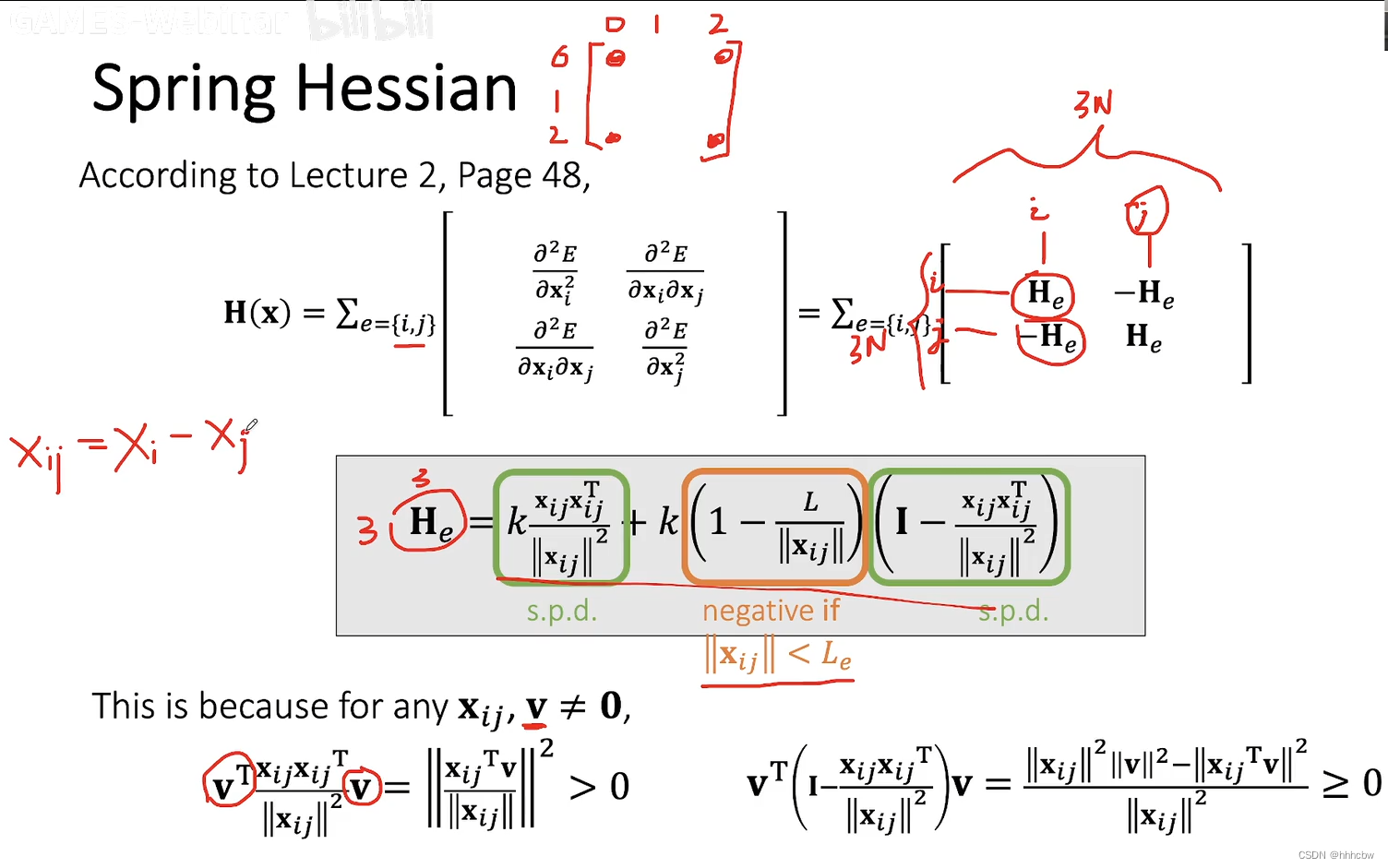
且 $△t$ 越小，左边的矩阵A越正定。

正定有唯一解，非正定不一定没有唯一解(不是必要条件)

而且当弹簧挤压的时候，其不一定向哪弯曲，所以非正定产生的现象也可解释。一维肯定正定。

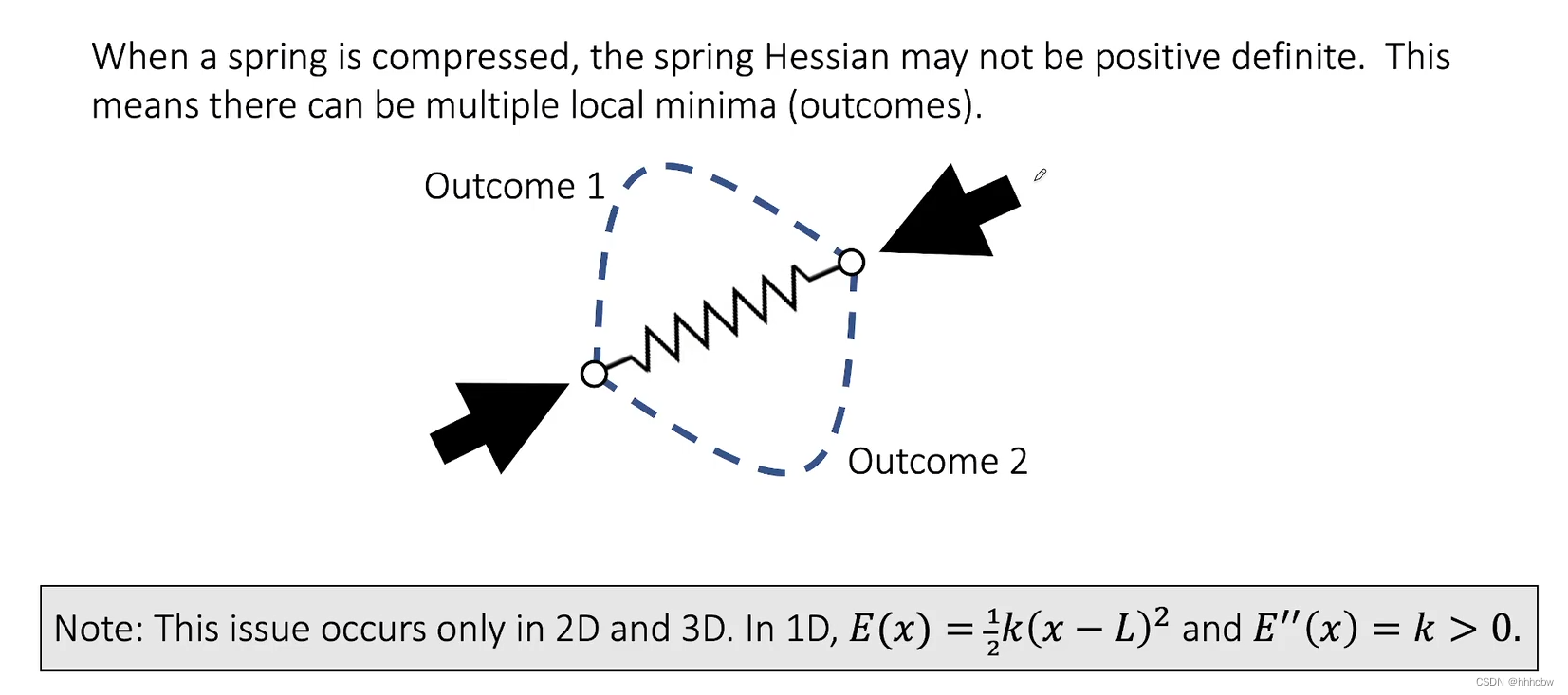
正定有时候是出于算法稳定性的角度考虑的，所以如果不正定，可以直接把后面的项删掉，保证正定(作业直接使用一个magic matrix)

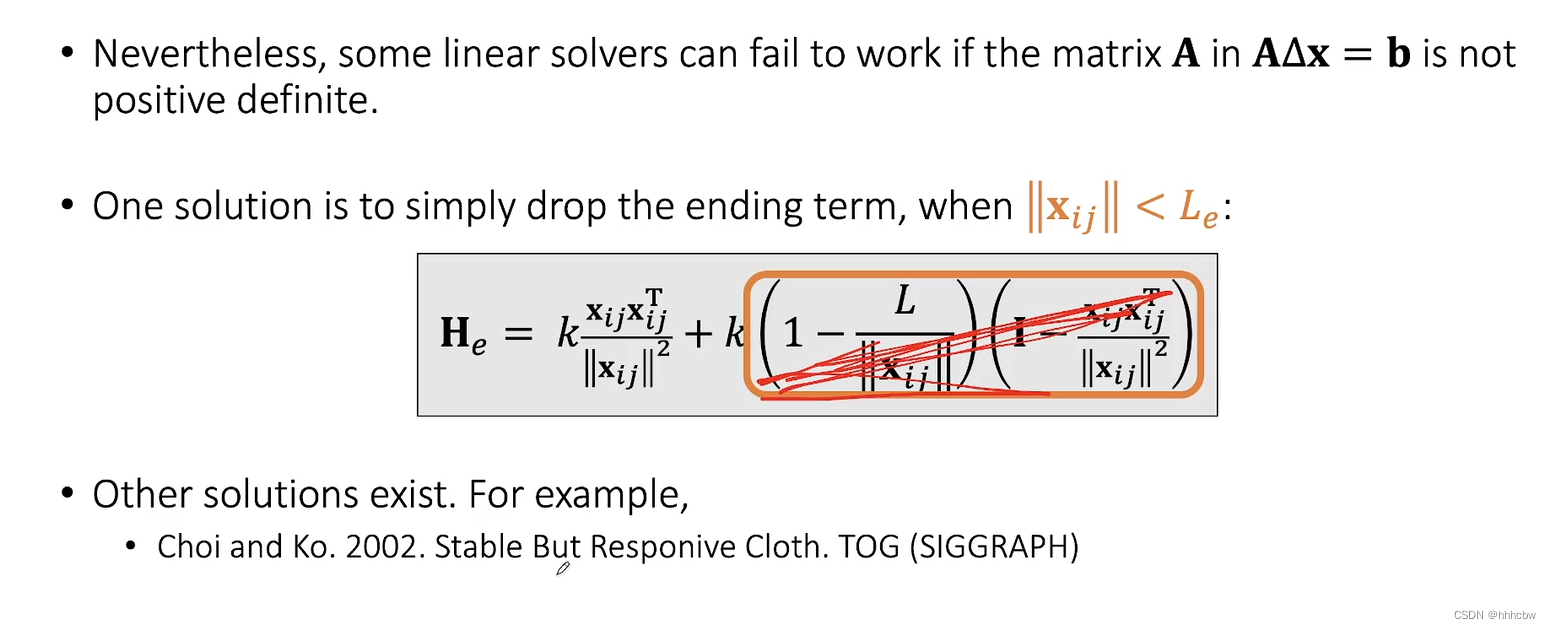
Jacobi迭代

上面我们通过牛顿法，把优化问题转化为解一个线性系统，解线性系统分为直接法(高斯消元等)与迭代法。直接法对 A 的要求小，适合在 CPU 上做，有一定内存开销。迭代法对 A 有一定要求，例如要求 A 正定，但可以在 GPU 上实现，有一些加速方法。

Jacobi迭代就是其中一种迭代法，$\alpha =1$要求 A 是对角占优的。$\alpha$ 取其他值，可以使对 A 的要求没那么高。

其可以使用切比雪夫加速

代码

这里的 G[] 取负号，就是等式右边的项

        float omega = 1.0f;
        for (int k = 0; k < 32; k++)
        {
            //if (k == 0) omega = 1.0f;
            //else if (k == 1) omega = 2.0f / (2.0f - rho * rho);
            //else omega = 4.0f / (4.0f - rho * rho * omega);

            Get_Gradient(X, X_hat, t, G);

            //Update X by gradient.
            for (int i = 0; i < X.Length; i++)
            {
                if (i == 0 || i == 20) continue;
                Vector3 new_x = omega * (X[i] + (1.0f / (mass / (t * t) + 4.0f * spring_k)) * -G[i]) + (1.0f-omega) * last_X[i];
                last_X[i] = X[i];
                X[i] = new_x;
            }
        }

Get_Gradient() 部分如下

    void Get_Gradient(Vector3[] X, Vector3[] X_hat, float t, Vector3[] G)
    {
        //Momentum and Gravity.
        for (int i = 0; i < X.Length; i++)
        {
            G[i] = mass * (X[i] - X_hat[i]) / (t * t) - mass * gravity;
        }
        //Spring Force.
        for (int e = 0; e < L.Length; e++)
        {
            int i = E[e * 2];
            int j = E[e * 2 + 1];
            G[i] = G[i] + spring_k * (1 - L[e] / (X[i] - X[j]).magnitude) * (X[i] - X[j]);
            G[j] = G[j] - spring_k * (1 - L[e] / (X[i] - X[j]).magnitude) * (X[i] - X[j]);
        }
    }

结果

---

Position Based Dynamics

刚度问题(Stiffness Issue)

真实世界中的布料拉伸超过一定程度后，对拉伸具有很强的抵抗。基于胡可定律的弹簧模型中需要增大弹性系数k来模拟这种现象，但这会造成显式积分和隐式积分都出现问题，增大了模拟计算量。基于约束的方法被提出的动机就是想要解决这个问题。

单个弹簧

假设弹簧的弹性系数无限大，那么弹簧的长度就成了一个约束，即弹簧的形变量 $\varphi (\vec{x})=0$，下图中的 $\Omega$ 是满足这个约束的空间。当约束被破坏时，KaTeX parse error: Expected '}', got 'EOF' at end of input: …c{x}={\vec{x_i},KaTeX parse error: Expected 'EOF', got '}' at position 10: \vec{x_j}}̲ 在 $\Omega$ 外，我们做一个投影操作把 $\vec{x}$ 以最近的距离移动到 $\Omega$ 的边界上使弹簧恢复原长。


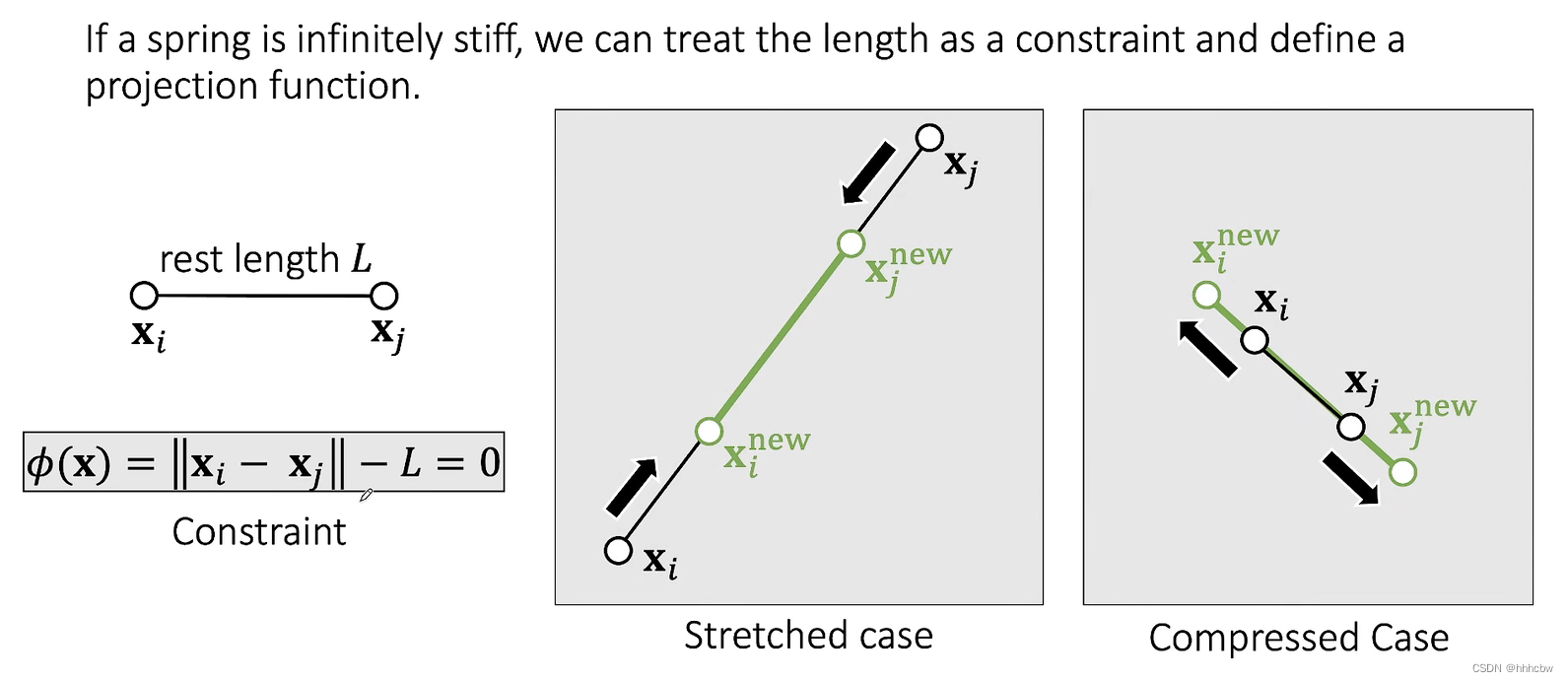
更新公式如下，其中 $m_i$ 是端点的质量，默认情况下两端质量相同，拉伸后两个端点都向着中心点移动。如果希望让其中一个端点被固定住不动，只需要把那个端点的质量设为无限大。

当然还可以加其他约束(比如弯曲力约束)，在实验中并没有考虑这些，就不细说了，想了解的可以进一步看PBD的论文。

多个弹簧

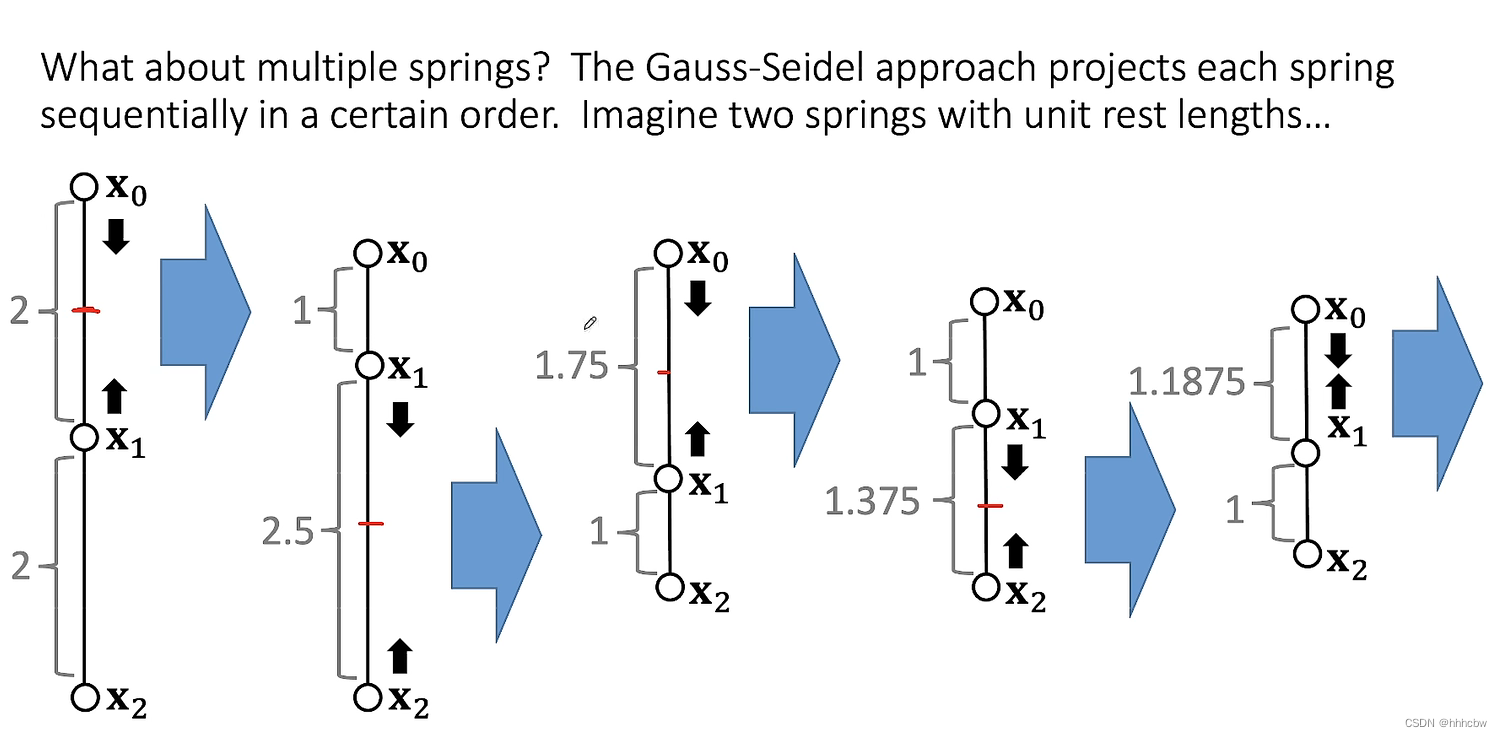
Guass-Seidel 方法

Guass-Seidel 方法就是依次按每个弹簧更新两个顶点的位置。 存在计算顺序影响最后结果的问题(可能会造成bias问题，整个布料歪向一边，也可能会影响算法收敛的速度)；迭代次数越多，越能更好地满足所有弹簧的约束。Gauss-Seidel方法虽然名字交 Gauss-Seidel，但与数学中的 Gauss-Seidel 其实不一样，实际所做操作更接近于随机梯度下降算法。

Jacobi 方法

对每个顶点的更新求和之后再取平均值，这就解决了偏向性问题，且容易并行

仿真过程

迭代次数越多，越没弹性；网格很大，需要更多次数的迭代才收敛，即弹性会变大。这里速度是叠加的原因是x已经是被速度更新后的x，所以计算差值的时候没有考虑原有的速度，所以要把原有的速度加上来

PBD的优点及缺点

• 优点：容易并行；容易实现；低分辨率效率高(一般1000个点以下效率很好)；通用性好；
• 缺点：没有物理解释；高分辨率效率不好。
  

代码

代码非常直观，就是一个对力求和取平均的过程。

    void Strain_Limiting()
    {
        Mesh mesh = GetComponent<MeshFilter>().mesh;
        Vector3[] vertices = mesh.vertices;
        Vector3[] sum_x = new Vector3[vertices.Length];
        int[] sum_n = new int[vertices.Length];
        //Apply PBD here.
        for (int i = 0; i < vertices.Length; i++)
        {
            sum_x[i] = new Vector3(0, 0, 0);
            sum_n[i] = 0;
        }
        for (int e = 0; e < L.Length; e++)
        {
            int i = E[e * 2];
            int j = E[e * 2 + 1];
            Vector3 xij = vertices[i] - vertices[j];
            sum_x[i] = sum_x[i] + 0.5f * (vertices[i] + vertices[j] + L[e] * xij * (1.0f / xij.magnitude));
            sum_x[j] = sum_x[j] + 0.5f * (vertices[i] + vertices[j] - L[e] * xij * (1.0f / xij.magnitude));
            sum_n[i]++;
            sum_n[j]++;
        }
        for (int i = 0; i < vertices.Length; i++)
        {
            if (i == 0 || i == 20) continue;
            V[i] = V[i] + (1.0f / t) * ((0.2f * vertices[i] + sum_x[i]) / (0.2f + (float)sum_n[i]) - vertices[i]);
            vertices[i] = (0.2f * vertices[i] + sum_x[i]) / (0.2f + (float)sum_n[i]);
        }
        mesh.vertices = vertices;
    }

结果