前言

本文记录自己刷，牛客网的面试必刷TOP101，地址：面试必刷TOP101–二分查找.排序。题目从BM17----BM22，总共有六道题目。

提示：以下是本篇文章正文内容

二分查找/排序

1、BM17 二分查找-I

题目：

请实现无重复数字的升序数组的二分查找。
给定一个元素升序的、无重复数字的整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标（下标从 0 开始），否则返回 -1。

代码实现：

public class BM17 {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * @param nums   int整型一维数组
     * @param target int整型
     * @return int整型
     */
    public int search(int[] nums, int target) {
        // write code here
        if (nums == null || nums.length < 1) {
            return -1;
        }
        int left = 0, right = nums.length - 1;
        int mid = 0;
        while (left <= right) {
            mid = left + (right - left) / 2;
            if (target == nums[mid]) {
                return mid;
            } else if (target < nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
}

2、BM18 二维数组中的查找

题目：

在一个二维数组array中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

代码实现：

public class BM18 {
    /**
     * @param target : 目标值
     * @param array  ： 二维数组
     * @return 返回是否能在二维数组中找到目标值，true就是可以找到目标值，false则为找不到目标值
     */
    public boolean Find(int target, int[][] array) {
        if (array == null || array[0].length == 0 || target < array[0][0]) {
            return false;
        }
        int m = array.length;// 二维数组行数
        int n = array[0].length; // 二维数组的列数
        // 从左上角开始找
        int i = 0, j = n - 1;
        while (i < m && j >= 0) {
            if (target == array[i][j]) {
                return true;
            } else if (target < array[i][j]) {
                j--;
            } else {
                i++;
            }
        }
        return false;
    }
}

3、BM19 寻找峰值

题目：

给定一个长度为n的数组nums，请你找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。
- 峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于。
- 假设 nums[-1] = nums[n] = −∞
- 对于所有有效的 i 都有 nums[i] != nums[i + 1]
- 可以使用O(logN)的时间复杂度实现此问题吗？

思路：

好的，我又不会了，我记得是用单调性，但是我不会啊。
参考视频：第十九天：寻找峰值;
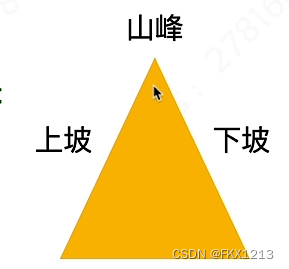
因为数组最左边的元素和最右边的元素都是负无穷大，所以元素维护的形状是一个山一样的，就分为两种情形：
- 上坡：上坡就一定会走到峰顶
- 下坡：下坡就不一定会走到峰顶
并且，必须在while循环的条件中，使用小于，当出现等于就跳出循环

代码实现：

public class BM19 {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * @param nums int整型一维数组
     * @return int整型
     */
    public int findPeakElement(int[] nums) {
        // write code here
        int left = 0, right = nums.length - 1;
        int mid = 0;
        //
        while (left < right) {
            mid = left + (right - left) / 2;
            if (nums[mid] < nums[mid + 1]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return right;
    }
}

4、BM20 数组中的逆序对

题目：

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。
输入一个数组,求出这个数组中的逆序对的总数P。
并将P对1000000007取模的结果输出。即输出P mod 1000000007。
要求：空间复杂度 O(n)，时间复杂度 O(nlogn)。

思路：

我还是不会，无语。
参考视频：小米，shopee都让现场手撕了｜ 51. 数组中的逆序对。
根据时间复杂度，就可以想到使用归并排序；
在最后将两个有序数组进行归并的时候，记录逆序对的个数；

代码实现：

public class BM20 {
    // 数组逆序对
    public int InversePairs(int[] array) {
        // 使用归并排序，记录逆序对
        mergeSort(array, 0, array.length - 1);
        return count;
    }

    int count = 0;

    public void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = left + (right - left) / 2;
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);
            merge(arr, left, mid, right);
        }
    }

    void merge(int[] arr, int left, int mid, int right) {
        int[] help = new int[right - left + 1];
        int index = 0;

        int i = left, j = mid + 1;
        while (i <= mid && j <= right) {
            if (arr[i] <= arr[j]) {
                help[index++] = arr[i++];
            } else {
                count += mid - i + 1;
                count %= 1000000007;
                help[index++] = arr[j++];
            }
        }
        while (i <= mid) {
            help[index++] = arr[i++];
        }
        while (j <= right) {
            help[index++] = arr[j++];
        }
        for (index = 0; index <= right - left; index++) {
            arr[left + index] = help[index];
        }
    }
    
}

5、BM21 旋转数组的最小数字

题目：

有一个长度为 n 的非降序数组，比如[1,2,3,4,5]，将它进行旋转，即把一个数组最开始的若干个元素搬到数组的末尾，变成一个旋转数组，比如变成了[3,4,5,1,2]，或者[4,5,1,2,3]这样的。
请问，给定这样一个旋转数组，求数组中的最小值。

思路：

对于这种旋转数组，最重要的就是找到旋转点；
二分取中间的值，和两端进行比较，比较后缩小区间范围。

代码实现：

public class BM21 {
    public int minNumberInRotateArray(int[] array) {
        int left = 0, right = array.length - 1;

        while (left < right) {
            int mid = left + (right - left) / 2;

            if (array[mid] > array[right]) {
                left = mid + 1;
            } else if (array[mid] < array[right]) {
                right = mid;
            } else {
                right--;
            }
        }

        return array[right];
    }
}

6、BM22 比较版本号

题目：

牛客项目发布项目版本时会有版本号，比如1.02.11，2.14.4等等。
现在给你2个版本号version1和version2，请你比较他们的大小
版本号是由修订号组成，修订号与修订号之间由一个"."连接。1个修订号可能有多位数字组成，修订号可能包含前导0，且是合法的。例如，1.02.11，0.1，0.2都是合法的版本号
每个版本号至少包含1个修订号。
修订号从左到右编号，下标从0开始，最左边的修订号下标为0，下一个修订号下标为1，以此类推。
比较规则：
- 一. 比较版本号时，请按从左到右的顺序依次比较它们的修订号。比较修订号时，只需比较忽略任何前导零后的整数值。比如"0.1"和"0.01"的版本号是相等的
- 二. 如果版本号没有指定某个下标处的修订号，则该修订号视为0。例如，“1.1"的版本号小于"1.1.1”。因为"1.1"的版本号相当于"1.1.0"，第3位修订号的下标为0，小于1
- 三. version1 > version2 返回1，如果 version1 < version2 返回-1，不然返回0.

思路：

这道题居然都需要想，真无语啊我。
将字符串划分为数组，比较大小。

代码实现：

public class BM22 {
    /**
     * @param version1 : 版本号一
     * @param version2 ： 版本号二
     * @return version1 > version2 返回1，如果 version1 < version2 返回-1，不然返回0.
     */
    public int compare(String version1, String version2) {
        // write code here
        // 分割版本号
        String[] v1 = version1.split("\\.");
        String[] v2 = version2.split("\\.");

        for (int i = 0; i < v1.length || i < v2.length; i++) {
            int x = i < v1.length ? Integer.valueOf(v1[i]) : 0;
            int y = i < v2.length ? Integer.valueOf(v2[i]) : 0;
            if (x < y) {
                return -1;
            } else if (x > y) {
                return 1;
            }
        }
        return 0;
    }
}