光栅化过程:将一系列变换后的三角形转换为像素的过程。
三角形在图形学中得到很多的应用。
- 最基础的多边形(边数最少)。
- 任何多边形都可以拆成三角形。
- 性质:三角形内部一定是平面的。三角形内外部定义非常清楚。
- 定义三个顶点后,三角形内可以插值。
光栅化中最重要的一步:判断三角形与一个像素(中心点)的位置关系
采样:
- 一个函数离散化的过程。
- 采样可以是一维,二维,三维的。光栅化属于二维采样。
光栅化的方法:
给一个三角形,来判断像素中心是否在三角形内。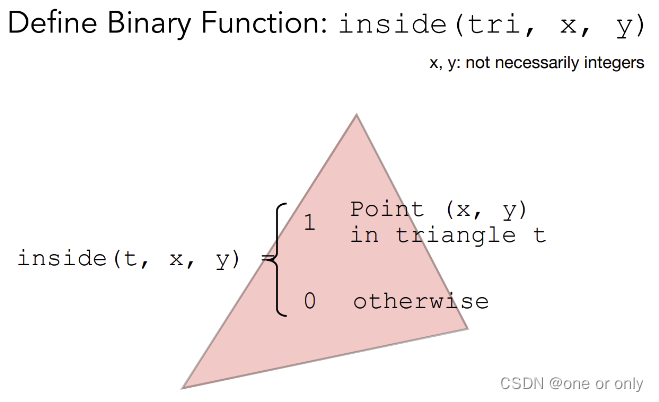
三角形转换为像素的过程,实际上就是判断像素跟三角形的关系。更确切地说,像素的中心点是否在三角形内。而一个点是否在三角形内,就可以使用向量的叉积方式判断。
for(int x = 0; x < xMax; ++x)
for(int y = 0; y < yMax; ++y)
image[x][y] = inside(tri, x + 0.5, y + 0.5);
通过上面的函数,我们就知道了坐标点(x, y)是否在在三角形内。这个求解的过程,我们一般将它称为采样(像素中心对屏幕的采样)。所以,采样通俗的理解就是给定一个线性函数,通过输入一些值,最后获得输出值的过程。
从上面的for循环,我们知道基本上是遍历了屏幕上的每个像素。在这里就可以做一个简单的优化。先判断是否在三角形所组成的长方形内(既取三角形的三个顶点横坐标和纵坐标的最小最大值)。我们就可以只判断长方形内的像素。
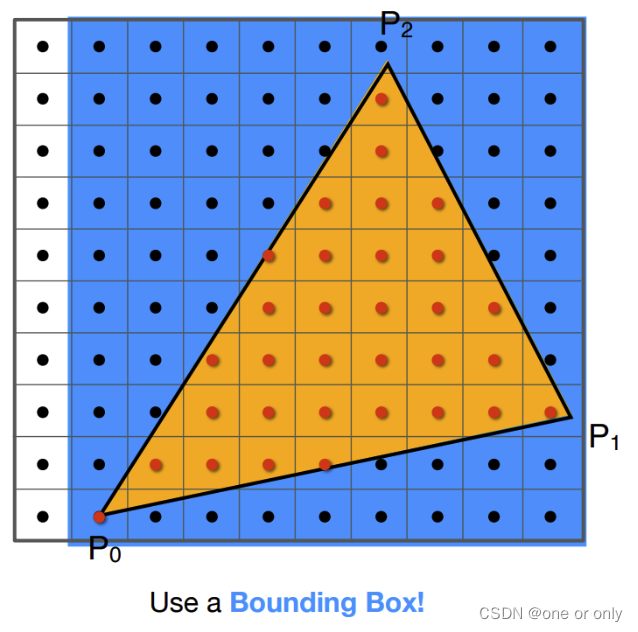
蓝色区域表示三角形的包围盒,只有在这个区域内的像素,才去做上面的for循环;即不需要每一个像素都从(0-width/height)走一遍)。
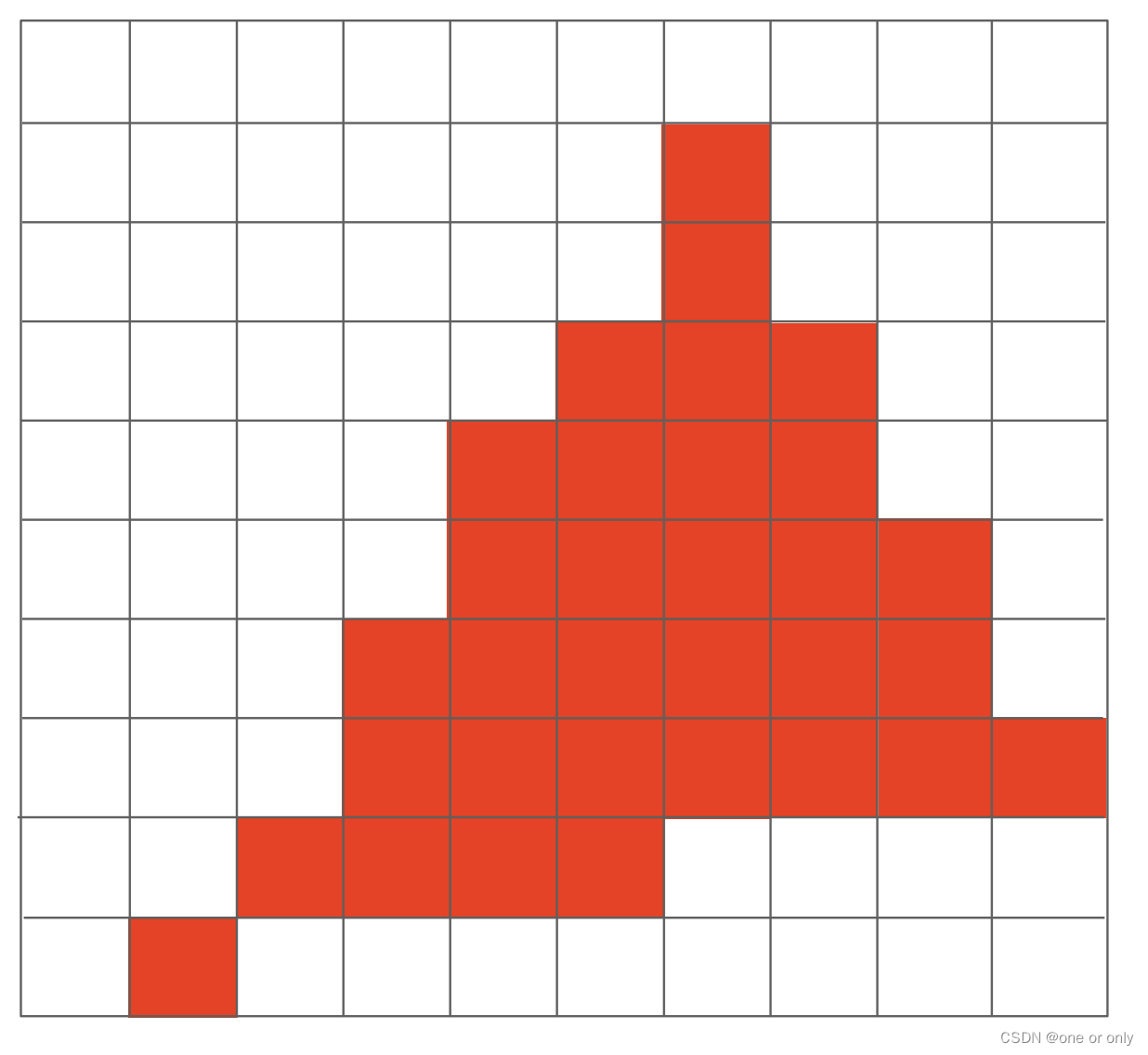
经过光栅化的过程,可以获得以下的结果。但是,以上的结果,明显比原本的三角形差的比较远,而且斜边不规则(这就是我们说的锯齿)。