邻接矩阵存储结构

• 用矩阵表示表示图中各个顶点之间的邻接关系和权值。如图$G=(V,E)$，其中有N个结点，使用$NxN$的矩阵表示。
  
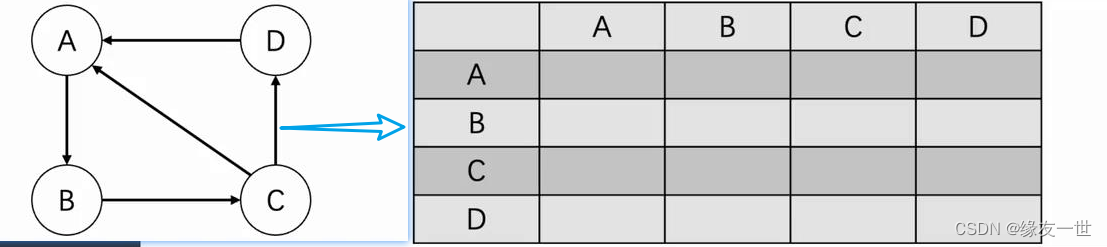
• 不带权值的图

$$G_{ij}=\{\begin{array}{l}1,无向图(v_i,v_j)或有向图的<v_i,v_j>是图中的边\\ 0,无向图的(v_i,v_j)或有向图的<v_i,v_j>不是图中的边\end{array}$$

• 举例
  
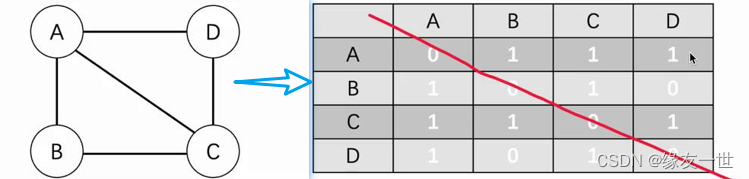
• 由于无向图没有方向之分，顶点之间是相互连接的，所以无向图的邻接矩阵必定是一个对称矩阵。
• 无向图的邻接矩阵是一个对称矩阵，存储时为节约时间，我们只存放上半部分。
• 带权值的图
  $$G_{ij}=\{\begin{array}{l}{w}_{ij},无向图的(v_i,v_j)或有向图<v_i,v_j>是图中的边\\ 0或\infty ,无向图的(v_i,v_j)或有向图的<v_i,v_j>不是图中的边\end{array}$$
  

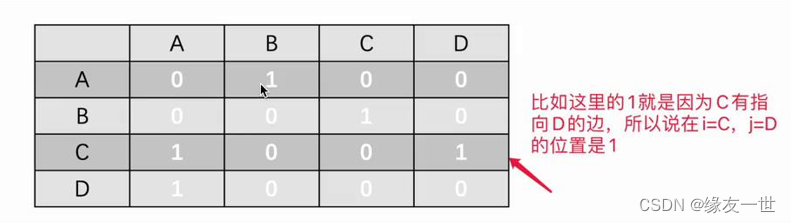
总结

• 对于无向图，邻接矩阵的第$i$行非$0$（或非$\infty$）的个数就是第$i$个顶点的度
• 对于有向图，邻接矩阵的第$i$行非$0$（或非$\infty$）的个数就是第$i$个顶点的出度（横向表示出度，纵向表示入度）

代码实现·有向图

#include<stdio.h>
#include<stdlib.h>
typedef char E;//定点存放的数据类型
#define MaxVertex 5
typedef struct MatrixGraph {
    int vertexCount;//顶点数
    int edgeCount;//边数
    int matrix[MaxVertex][MaxVertex];//矩阵的长，宽
    E data[MaxVertex];//各个顶点对应的数据
}* Graph;

//创建矩阵
Graph Create();
//添加各个顶点的数据
void addVertex(Graph graph,E element);
//存储边的关系
void addEdge(Graph graph,int i,int j);

#include "Map.h"
//创建矩阵
Graph Create() {
    //将结构体创建出来，注意使用动态内存，否则函数结束，栈空间会被回收
    //结构体中的数组也会创建出来
    Graph graph= (Graph)malloc(sizeof(struct MatrixGraph));
    graph->vertexCount=0;
    graph->edgeCount=0;
    //因为内存中的数据随机值，所以将其初始化为0，方便后续的使用
    for(int i=0;i<MaxVertex;i++) {
        for(int j=0;j<MaxVertex;j++) {
            graph->matrix[i][j]=0;
        }
    }
    return graph;
}

//添加各个顶点的数据
void addVertex(Graph graph,E element) {
    //当结点数量大于等于节点数时，结束函数
    if(graph->vertexCount>=MaxVertex) return;
    //采用后置加加的方式，将元素存储进去
    graph->data[graph->vertexCount++]=element;
}

//存储边的关系
void addEdge(Graph graph,int i,int j) {
    //初始化时已经将全部的数据置为0
    if(graph->matrix[i][j]==0) {
        //注意如果时无向图的话，就将[i][j]和[j][i]都置为1
        graph->matrix[i][j]=1;
        graph->edgeCount++;//边的条数+1
    }
}
//打印邻接矩阵
void printGraph(Graph graph) {
    for(int i=-1;i<graph->vertexCount;i++) {
        for(int j=-1;j<graph->vertexCount;j++) {
            if(j==-1) {//打印第一行的字母
                printf("%c",'A'+i);
            }else if(i==-1) {//打印从第二行起的首字母
                printf("%3c",'A'+j);
            }else {//打印矩阵的内容
                printf("%3d",graph->matrix[i][j]);
            }
        }
        putchar('\n');
    }
}

#include "Map.h"
int main() {
    Graph graph=Create();
    for(int c='A';c<='D';c++)
        addVertex(graph,(char)c);
    addEdge(graph,0,1);//A->B
    addEdge(graph,1,2);//B->C
    addEdge(graph,2,3);//C->D
    addEdge(graph,3,0);//D->A
    addEdge(graph,2,0);//C->A
    printGraph(graph);
    return 0;
}

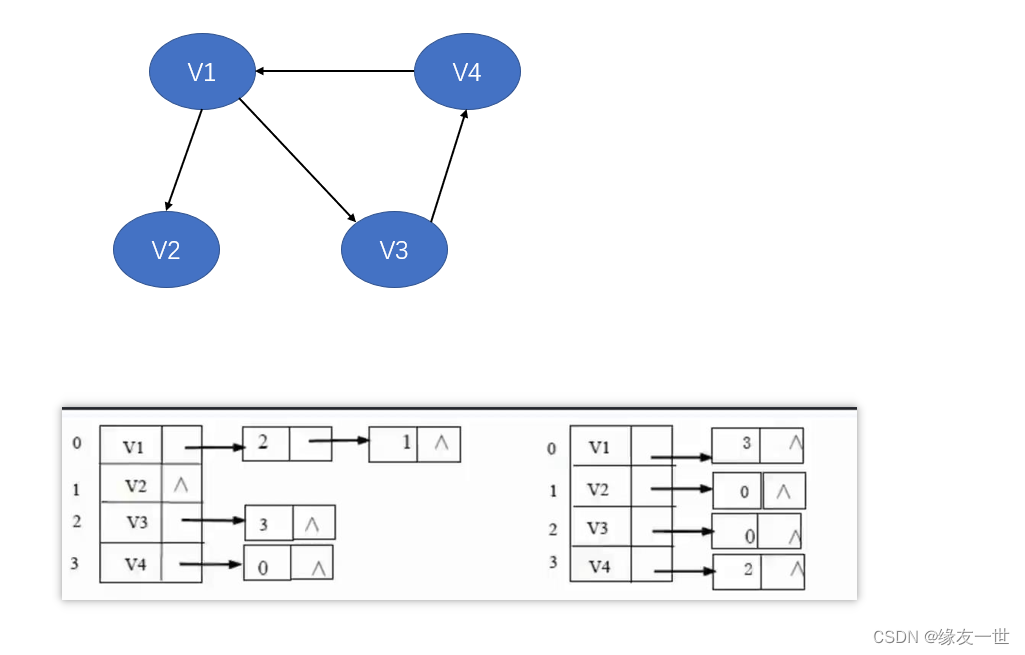
邻接表

• 对于图中的每个顶点。建立一个数组，存放一个头结点，与其邻接的顶点相连。
• 有向图
  
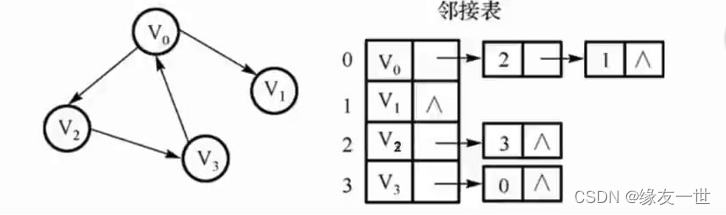
• 无向图
  

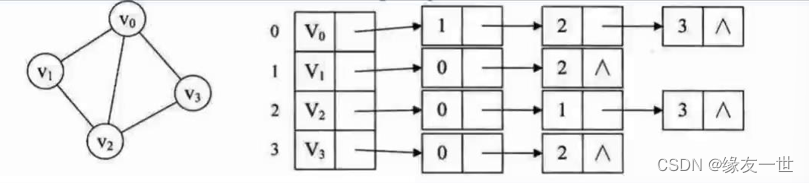
代码实现·有向图

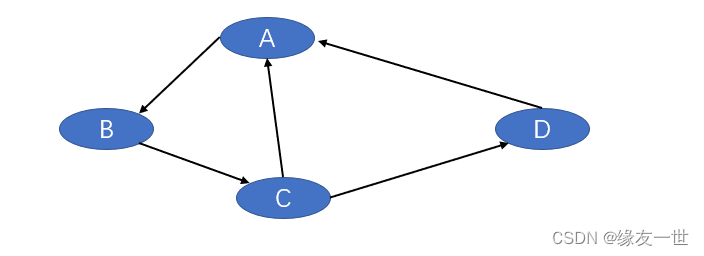
#include <stdio.h>
#include <stdlib.h>
#define MaxVertex 5
typedef char E;
//结点和头节点分开定义，普通结点记录邻接顶点信息
typedef struct node {
    int nextVertex;
    struct node *next;
} *Node;
//头节点记录元素
struct HeadNode {
    E element;
    struct node * next;
};

typedef struct AdjacencyGraph {
    int vertexCount;//顶点数
    int edgeCount;//边数
    struct HeadNode vertex[MaxVertex];
}* Graph;
//初始化
Graph create();
//添加顶点
void addVertex(Graph graph,E element);
//添加边的关系
void addEdge(Graph graph,int a,int b);
//打印邻接表
void printGraph(Graph graph);

#include "Map2.h"
//创建
Graph create() {
    Graph graph=(Graph) malloc(sizeof(struct AdjacencyGraph));
    graph->vertexCount=graph->edgeCount=0;
    return graph;
};
//添加顶点
void addVertex(Graph graph,E element) {
    if(graph->vertexCount>=MaxVertex) return;
    //添加新节点
    graph->vertex[graph->vertexCount].element=element;
    graph->vertex[graph->vertexCount].next=NULL;
    graph->vertexCount++;//顶点数更新
}
void addEdge(Graph graph,int a,int b) {
    //定义一个指向链表的头结点的下一结点指向
    Node node=graph->vertex[a].next;
    //开辟顶点空间
    Node newNode=(Node) malloc(sizeof(struct node));
    newNode->next=NULL;
    newNode->nextVertex=b;
    //如果头结点下面没有东西，就直接连接；否则，就遍历到最后一个结点后，添加新节点
    if(!node) {
        graph->vertex[a].next=newNode;//注意这里不能使用node，因为我们要真实地改变头节点的next指向
    }else {
        do{
            //如果已经连接到对应的结点，直接返回
            if(node->nextVertex==b) {
                free(newNode);
                newNode=NULL;
                return ;
            }
            //否则一直遍历到最后一个结点
            if(node->next) node=node->next;
            else break;//如果遭到了最后一个结点，直接结束
        }while(true);
        node->next=newNode;
    }
    graph->edgeCount++;//边数计数+1
}
//打印
void printGraph(Graph graph) {
    for(int i=0;i<graph->vertexCount;i++) {
        printf("%d | %c",i,graph->vertex[i].element);
        Node node=graph->vertex[i].next;
        while(node) {
            printf("-> %d",node->nextVertex);
            node=node->next;
        }
        printf("\n");
    }
}

#include "Map2.h"
int main() {
    Graph graph=create();
    for(int c='A';c<='D';c++) {
        addVertex(graph,(char)c);
    }
    addEdge(graph,0,1);//A->B
    addEdge(graph,1,2);//B->C
    addEdge(graph,2,3);//C->D
    addEdge(graph,3,0);//D->A
    addEdge(graph,2,0);//C->A
    printGraph(graph);
}

• 缺点：无法快速计算顶点的入度数。
• 解决方法：再用一组邻接表，专门记录入度的关系。
  

总结

• 邻接矩阵：适合稠密图
• 邻接表：适合稀疏图