目录
题目来源
题目描述
示例
提示
题目解析
算法源码
题目来源
239. 滑动窗口最大值 - 力扣(LeetCode)
题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例
| 输入 | nums = [1,3,-1,-3,5,3,6,7], k = 3 |
| 输出 | [3,3,5,5,6,7] |
| 说明 | 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7 |
| 输入 | nums = [1], k = 1 |
| 输出 | [1] |
| 说明 | 无 |
提示
- 1 <= nums.length <= 10^5
- -10^4 <= nums[i] <= 10^4
- 1 <= k <= nums.length
题目解析
本题最简单的思路其实就是定义一个长度为k的滑窗,然后每次求滑窗范围内最大值,但是这样的算法的时间复杂度为O((n - k + 1) * k),因此算法的性能比较差。
本题最佳解题思路是:单调队列。
单调队列在此处是用于维护滑窗的最大值的。
如下图是用例1的滑窗运动过程,和单调队列的变化

滑窗运动过程分为两块:
- 初始滑窗的形成过程(即只有新增尾部元素的过程)
- 滑窗的右移过程(即失去一个头部(绿色)元素,新增一个尾部元素)
我们假设滑窗的尾巴元素是tail,而新加入滑窗的元素是new,那么为了维护单调队列的单调性,本题是单调递减,只要滑窗的tail < new,那么就必须将tail出队,然后继续比较滑窗的新tail和new,直到滑窗的tail >= new了,或者滑窗为空了,此时将new加入到滑窗尾部。
上面逻辑对应单调队列的尾删操作、以及尾增操作。
另外,单调队列还有一个非常重要的头删操作。比如上图中如下两个过程
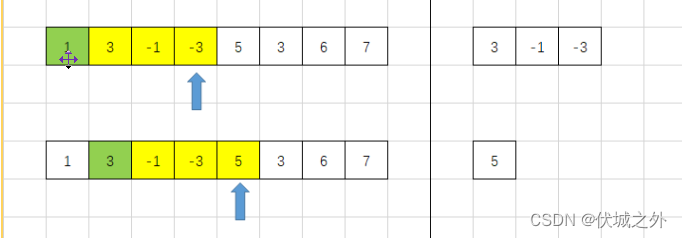
新滑窗失去了3元素,新增了5元素,那么其实此时单调队列[3, -1, -3]按顺序需要做如下两件事:
- 先删除队列的头元素3,此时单调队列变为[-1, -3]
- 然后再加入5到队列,此时单调队列变为[-1, -3, 5],为了维护单调性,因此依次尾删-3、-1,最后单调队列就只有[5]
从这个过程,我们发现单调队列中3元素,并不是为了维护单调性而被尾删的,而是被头删的。
为什么呢?
从上图两个黄色的滑窗,我们可以发现,滑窗移动过程中,失去了3元素,因此新滑窗需要删掉3元素。
这里我们可以对比下面过程来分析

上图中新滑窗失去了1元素,但是单调队列[3, -1]却没有执行头删,这是因为单调队列的头部元素3还在新滑窗中,因此不需要头删。
因此,只有新滑窗失去的元素 == 单调队列的头部元素 时,我们才需要进行单调队列的头删操作。
Java算法源码
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// queue 是单调队列
LinkedList<Integer> queue = new LinkedList<>();
// ans 记录题解,一共有nums.length - k + 1滑窗
int[] ans = new int[nums.length - k + 1];
// j 记录当前滑窗的序号
int j = 0;
// 初始滑窗
for (int i = 0; i < k; i++) {
while (queue.size() > 0 && queue.getLast() < nums[i]) {
queue.removeLast();
}
queue.add(nums[i]);
}
ans[j++] = queue.getFirst();
// 后续滑窗
for (int i = k; i < nums.length; i++) {
// nums[i-k] 是滑窗失去的元素
if (nums[i - k] == queue.getFirst()) {
queue.removeFirst(); // 单调队列头删
}
// nums[i] 是滑窗新增的元素
while (queue.size() > 0 && queue.getLast() < nums[i]) {
queue.removeLast(); // 单调队列尾删
}
queue.add(nums[i]); // 单调队列尾增
ans[j++] = queue.getFirst();
}
return ans;
}
}
JavaScript算法源码
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var maxSlidingWindow = function(nums, k) {
const queue = [];
const ans = [];
for(let i=0; i<k; i++) {
while(queue.length && queue.at(-1) < nums[i]) {
queue.pop();
}
queue.push(nums[i]);
}
ans.push(queue[0]);
for(let i=k; i<nums.length; i++) {
if(nums[i-k] == queue[0]) {
queue.shift();
}
while(queue.length && queue.at(-1) < nums[i]) {
queue.pop();
}
queue.push(nums[i]);
ans.push(queue[0]);
}
return ans;
};
上面JS使用的数组模拟的双端队列,因此shift()操作的性能非常差,下面代码中,我模拟了一个双端队列MyQueue,包含头部出队shift,尾部出队pop,尾部入队push,以及获取双端队列头部first和尾部值last。
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var maxSlidingWindow = function(nums, k) {
const queue = new MyQueue();
const ans = [];
for(let i=0; i<k; i++) {
while(queue.length && queue.last() < nums[i]) {
queue.pop();
}
queue.push(nums[i]);
}
ans.push(queue.first());
for(let i=k; i<nums.length; i++) {
if(nums[i-k] == queue.first()) {
queue.shift();
}
while(queue.length && queue.last() < nums[i]) {
queue.pop();
}
queue.push(nums[i]);
ans.push(queue.first());
}
return ans;
};
class MyQueue{
constructor() {
this.head = null;
this.tail = null;
this.length = 0;
}
push(val) {
const node = new Node(val);
if(this.length == 0) {
this.head = node;
this.tail = node;
} else {
this.tail.next = node
node.prev = this.tail
this.tail = node
}
this.length += 1;
}
pop() {
if(this.length > 0) {
this.tail = this.tail.prev;
if(this.tail) this.tail.next = null;
this.length -= 1;
}
}
shift() {
if(this.length > 0) {
this.head = this.head.next;
if(this.head) this.head.prev = null;
this.length -= 1;
}
}
last() {
return this.tail.val;
}
first() {
return this.head.val;
}
}
class Node {
constructor(val) {
this.val = val;
this.prev = null;
this.next = null;
}
}
Python算法源码
from collections import deque
class Solution(object):
def maxSlidingWindow(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
# dq 是单调队列
dq = deque()
# ans 记录题解,一共有nums.length - k + 1滑窗
ans = []
# 初始滑窗
for i in range(k):
while len(dq) > 0 and dq[-1] < nums[i]:
dq.pop()
dq.append(nums[i])
ans.append(dq[0])
# 后续滑窗
for i in range(k, len(nums)):
# nums[i-k] 是滑窗失去的元素
if nums[i - k] == dq[0]:
dq.popleft() # 单调队列头删
# nums[i] 是滑窗新增的元素
while len(dq) > 0 and dq[-1] < nums[i]:
dq.pop() # 单调队列尾删
dq.append(nums[i]) # 单调队列尾增
ans.append(dq[0])
return ans