1参考

1.1根轨迹图的绘制及分析
1.2计算机控制技术01-3.4离散系统的根轨迹分析法
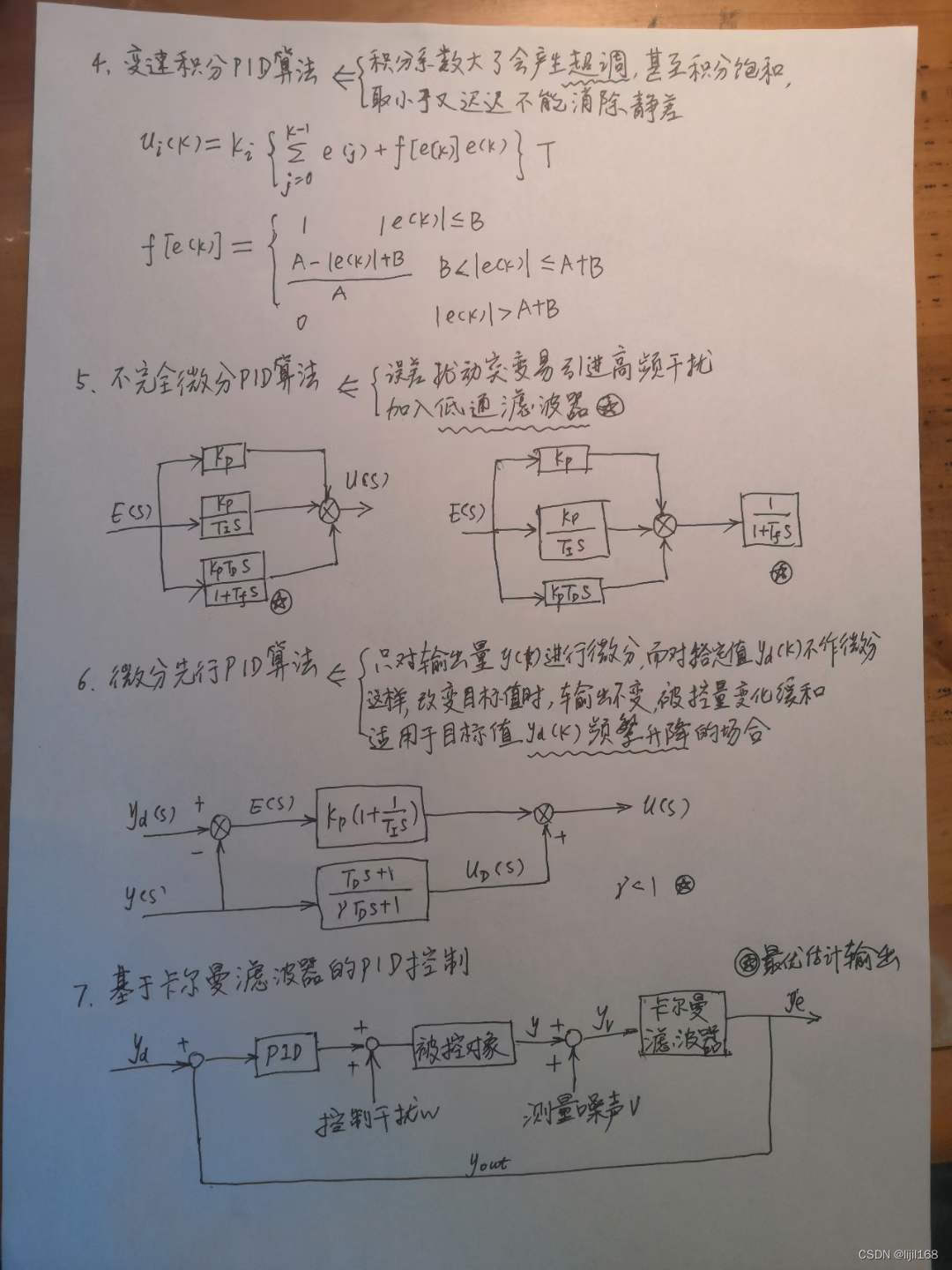
1.3PID控制算法学习笔记

2连续Ziegler-Nichols方法的PID整定

2.1整定方法

基于稳定性分析的频域响应PID整定方法：对于给定的被控对象传递函数，可以得到其根轨迹，对应穿越jw轴的点，增益Km为系统开始振荡时的增益K值，wn为振荡频率。
整定公式为：
kp=0.6 * km;
ki=kp * wm/pi;
kd=kp * pi/(4*wm);

2.2仿真示例

整定程序：

%PID Controler Based on Ziegler-Nichols
clear all;
close all;
sys=tf(400,[1,30,200,0]);
figure(1);
rlocus(sys);%画根轨迹图
[km,pole]=rlocfind(sys);%手动！！找系统开始震荡时的增益Km和对应的极点（穿越jw虚轴）
wm=imag(pole(2));%震荡频率

%由系统开始震荡时的增益Km和频率wn确定PID参数：
kp=0.6*km;
ki=kp*wm/pi;
kd=kp*pi/(4*wm);

figure(2);
grid on;
bode(sys,'r');
sys_pid=tf([kd,kp,ki],[1,0]);%PID控制器的传函
sysc=series(sys,sys_pid);%被控系统加上PID整定后的系统！！！
hold on;
bode(sysc,'b');

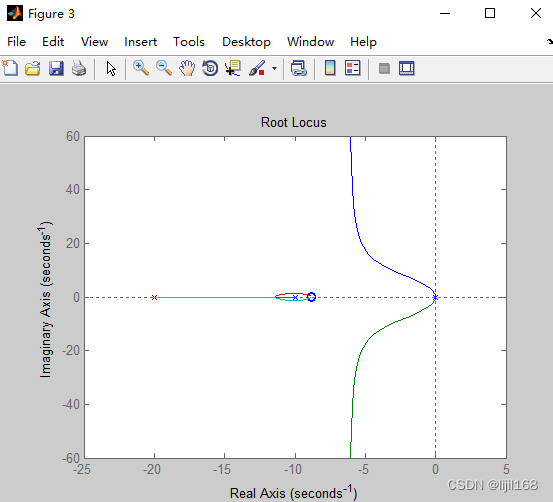
figure(3);
rlocus(sysc);

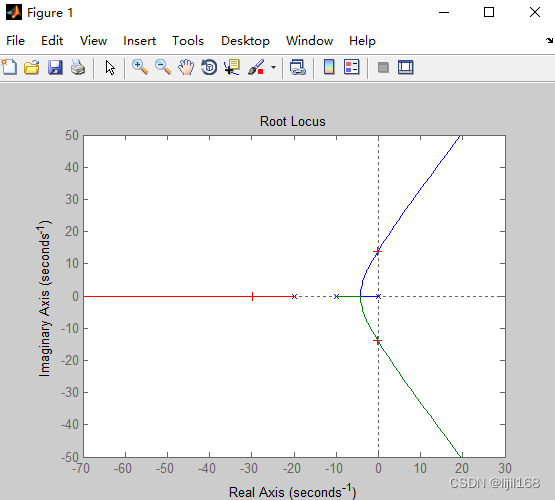
整定前系统根轨迹图见Figure1，系统有3个极点，根轨迹图有3根，从极点开始，终止与无限远（因为系统无0点，否则有终止于0点的线），**[km,pole]=rlocfind(sys);%手动！！找系统开始震荡时的增益Km和对应的极点（穿越jw虚轴）**当用鼠标选取与虚轴相交的点时，找到系统振荡开始的增益Km=14,对应的极点有三个（红色的点），振荡频率wm=14rad/s，根据整定公式可得Kp=8.8371;Ki=39.4847;Kd=0.4945。

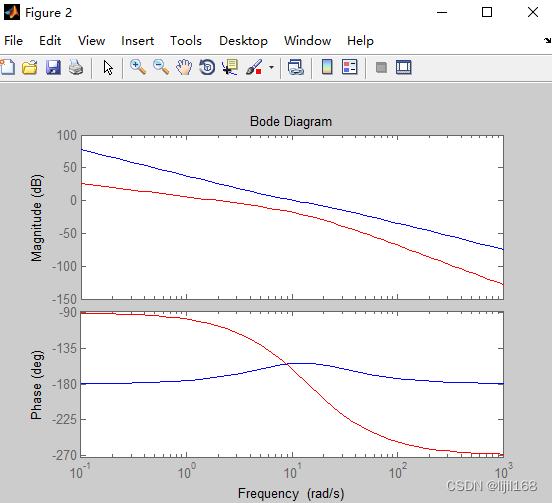
整定前后的系统伯德图见Figure2，整定后，频带拓宽，相移超前。

整定后的系统根轨迹图见Figure3，所有极点位于负半平面，系统达到完全稳定状态。