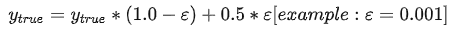闭包是一个新的关系，这个新的关系是由旧关系构造的

1、闭包(closure)的定义

包含一些给定对象，具有指定性质的最小集合

定义： 设R是集合 A 上的关系，若存在关系 R 的具有性质 P 的闭包，则此闭包是集合 A 上包含R的具有性质 P 的关系 S，并且 S 是每一个包含R的具有性质 P 的 A×A 的子集

❗ 简单来说，求 R 的具有性质P的闭包就是把R 与满足性质 P 的关系的集合取并（∪）

2、不同类型的闭包

1. 自反闭包(reflexive closure)

自反闭包： 包含给定关系R的最小自反关系，称为R的自反闭包。记作 r ( R )

(1) R ⊆ r( R )
(2) r( R )是自反的
(3) ∀S( (R⊆S ∧ S自反) → r( R )⊆S )

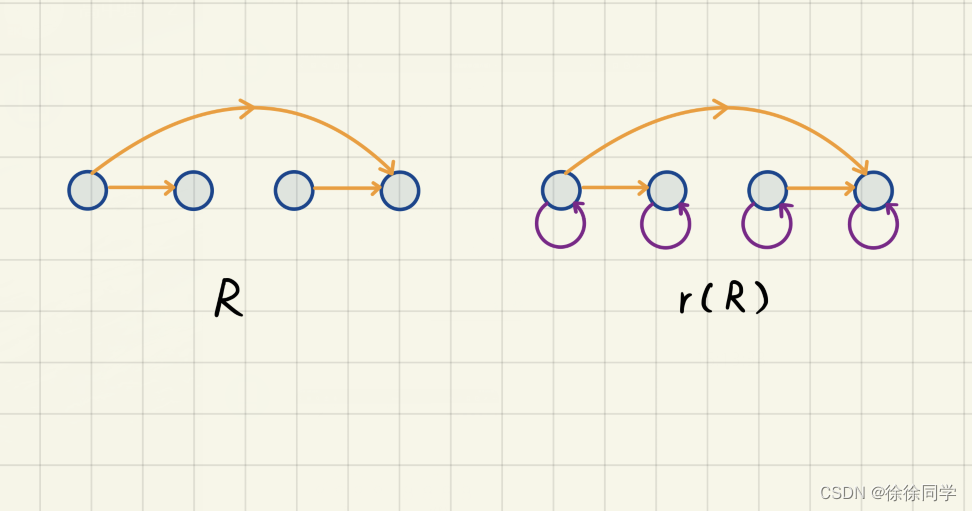
！ 加上自己到自己的环

📘例：
整数集上的关系R={ (a，b) l a < b } 的自反闭包是什么？

解：
R的自反闭包是 { (a,b) l a < b } U { (a,a) l a∈Z } = { (a,b) l a ≤ b }

2. 对称闭包(symmetric closure)

对称闭包： 包含给定关系R的最小对称关系，称为R的对称闭包。记作s( R )

(1) R ⊆ s( R )
(2) s( R )是对称的
(3) ∀S( (R⊆S ∧ S对称) → s( R )⊆S )

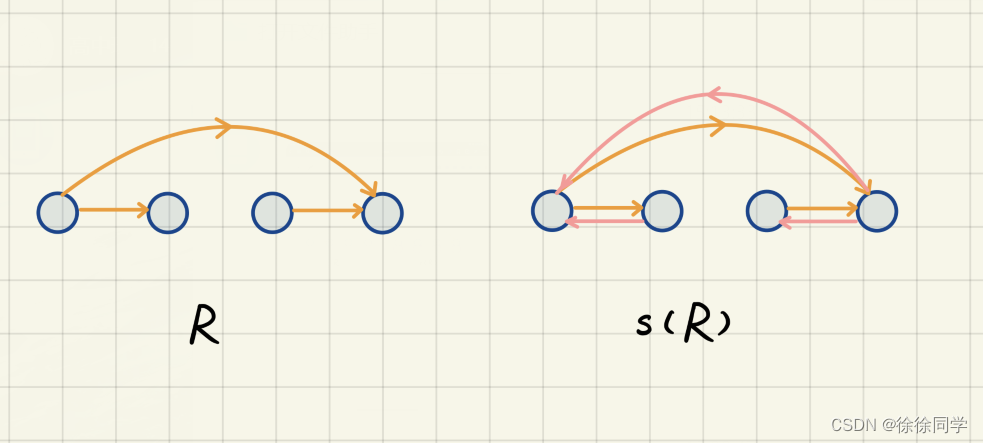
！ 每条边有回路

3. 传递闭包(transitive closure)

传递闭包： 包含给定关系R的最小传递关系，称为R的传递闭包。记作t( R )

(1) R ⊆ t( R )
(2) t ( R )是传递的
(3) ∀S( (R⊆S ∧ S传递) → t( R )⊆S )

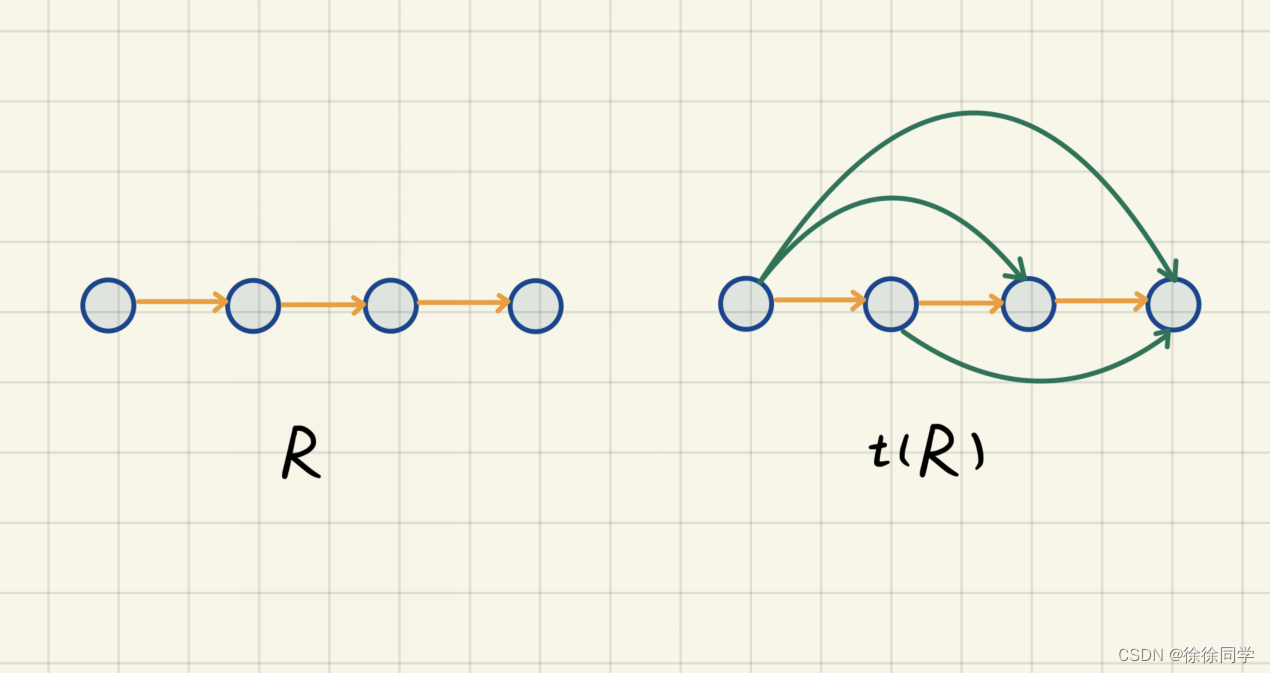
3、闭包的几个定理

定理1

设 R ⊆ A × A 且 A ≠ ∅，则

(1) R自反 ⇔ r( R ) = R
(2) R对称 ⇔ s( R ) = R
(3) R传递 ⇔ t( R ) = R

证明：
(1) R ⊆ R ∧ R自反 ⇒ r( R ) ⊆ R
又 R ⊆ r( R )
∴ r( R ) = R

(2)(3) 完全类似

定理2

设 R₁⊆R₂⊆A×A 且 A≠∅, 则

(1) r( R₁ ) ⊆ r( R₂ )
(2) s( R₁ ) ⊆ s( R₂ )
(3) t( R₁ ) ⊆ t( R₂ )

证明：
(1) R₁⊆R₂ ⊆ r( R₂ )自反，
∴ r( R₁ ) ⊆ r( R₂ )

(2)(3) 类似

定理3 - R1∪R2

设 R₁，R₂⊆A×A 且 A≠∅, 则

(1) r( R₁∪R₂) = r( R₁ )∪r( R₂ )
(2) s( R₁∪R₂ ) = s( R₁ )∪s( R₂)
(3) t( R₁∪R₂) ⊇ t( R₁ )∪t( R₂ )

证明(1)：
(1) r( R₁∪R₂) = r( R₁ )∪r( R₂ )

利用定理2，
r( R₁∪R₂) ⊇ r( R₁)∪r(R₂)
r( R₁)∪r(R₂)自反且包含 R₁∪R₂
∴ r( R₁∪R₂) ⊆ r( R₁)∪r(R₂)
∴ r( R₁∪R₂) = r( R₁ )∪r( R₂ )

证明(2)：
(2) s( R₁∪R₂ ) = s( R₁ )∪s( R₂)

利用定理2,
s(R₁∪R₂ ) ⊇ s(R₁ )∪s(R₂ )
s(R₁)∪s(R₂ )对称且包含R₁∪R₂
∴ s(R₁∪R₂ ) ⊆ s(R₁)∪s(R₂)
∴ s( R₁∪R₂ ) = s(R₁ )∪s( R₂ )

证明(3)：
(3) t( R₁∪R₂) ⊇ t( R₁ )∪t( R₂ )
利用定理2
t(R₁∪R₂ )⊇t(R₁ )∪t(R₂ ).
反例: t(R₁∪R₂ )⊃t(R₁ )∪t(R₂ )
简单来说，R₁并R₂后，有可能边增加了，自然传递关系会增加

定理4

设 R ⊆ A×A 且 A≠∅, 则

(1) r( R ) = R∪I_A （I_A是A的自反关系）
(2) s( R ) = R∪R_-1
(3) t( R ) = R∪R²∪R³∪…

(3)的推论：设 R⊆A×A 且 0<|A|<∞（A是有穷集）， 则∃l ∈N, 使
得 t( R ) = R∪R²∪R³∪…∪R^l ;

对比：
R自反 ⇔ I_A⊆R
R对称 ⇔ R=R^-1
R传递 ⇔ R₂⊆R

定理5

设R⊆A×A且A≠∅，则

(1) R自反 ⇒ s( R )和t( R )自反
(2) R对称 ⇒ r( R )和t( R )对称
(3) R传递 ⇒ r( R )传递

📘例题：

设 A = { a,b,c,d }，R = { <a,b>,<b,a>,<b,c>,<c,d> }
求 r( R ), s( R ), t( R )

解：

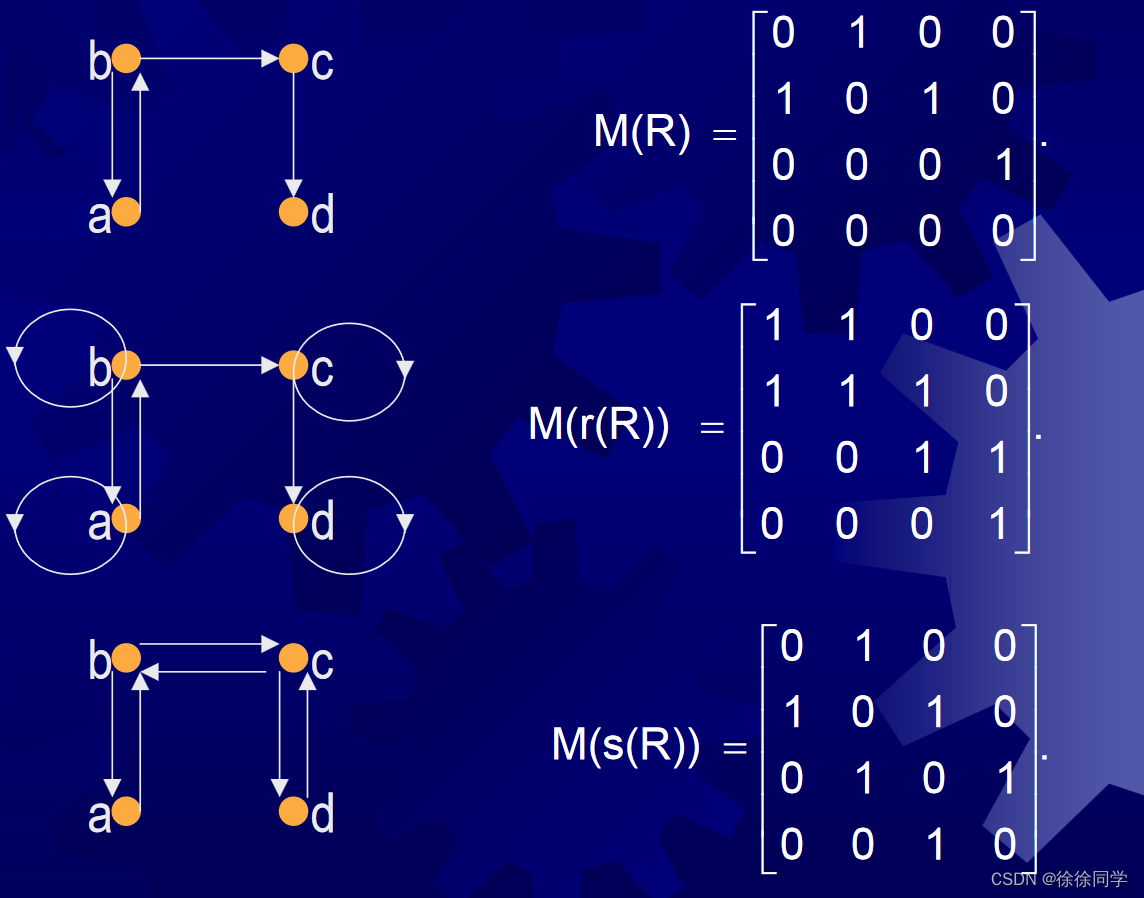求传递闭包：

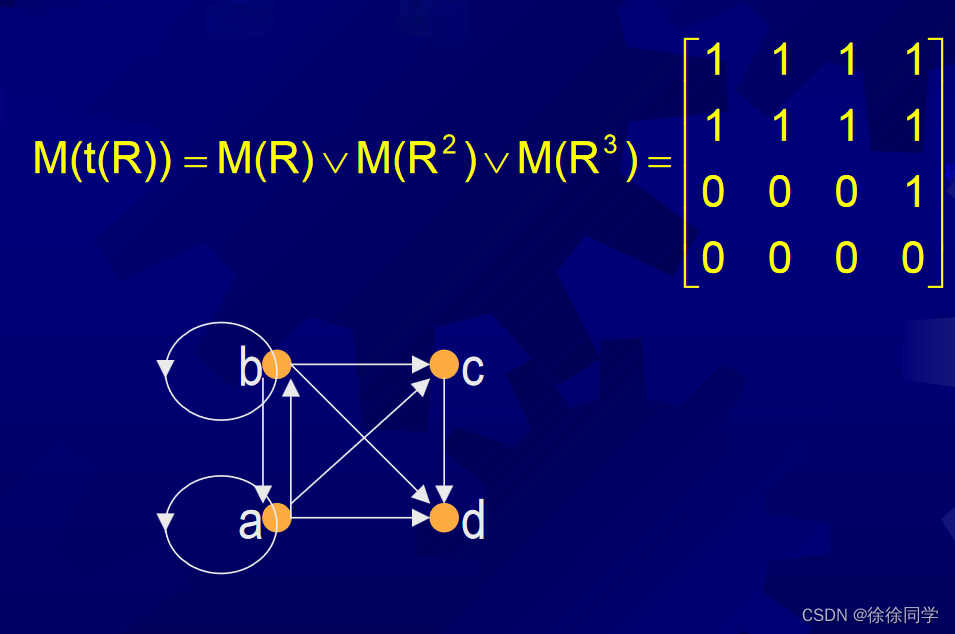
4、有向图中的路径

路径：设R是集合A上的关系。从a到b存在一条长为n(n为正整数)的路径，当且仅当(a，b)∈Rⁿ

回路：开始和结束于同一顶点

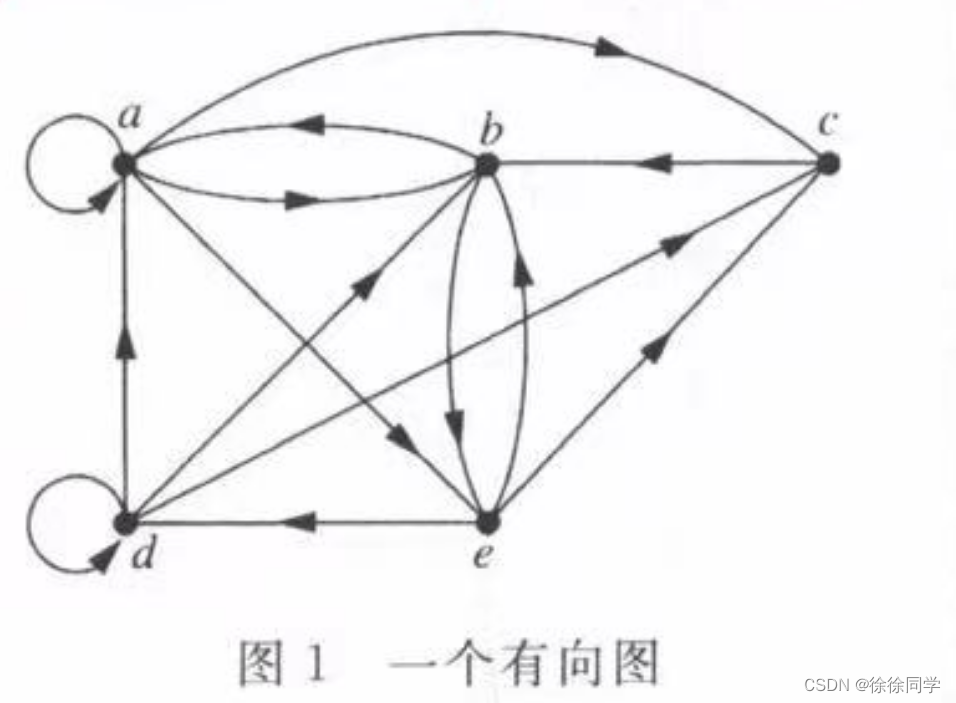
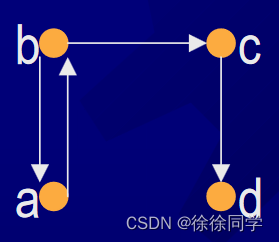
下面哪些是图1中的有向图中的路径？

①a，b，e，d
②a，e，c，d，b
③b，a，c，b，a，a，b
④d，c
⑤c，b，a
⑥e，b，a，b，a，b，e
这些路径的长度是多少？
哪些路径是回路?

解：
因为(a，b)、(b，e)和(e，d)都是边，所以①a，b，e，d是长为3的路径。

因为(c，d)不是边，所以②a，e，c，d，b 不是路径。

因为(b，a)、(a，c)、(c，b)、(b，a)、(a，a)和（a，b)都是边，所以③b，a，c，b，a，a，b 是长为6的路径

同理，因为(d，c)是边，所以④d，c是长为1的路径。

(c，b)和(b，a)是边，所以⑤c，b，a是长为2的路径。

(e，b)、(b，a)、(a，b)、(b，a)、(a，b)、(b，e)都是边，因此⑥e，b，a，b，a，b，e是长为6的路径。

只有两条路径
③b，a，c，b，a，a，b和⑥e，b，a，b，a，b，e是回路，因为它们开始和结束于同一顶点

5、传递闭包

1. 连通性关系

设R是集合A上的关系。连通性关系 R^* 由形如 (a，b) 的有序对构成，使得在关系R中，从顶点 a 到 b 之间存在一条长度至少为1的路径

因为 Rⁿ 由有序对(a，b)构成，使得存在一条从顶点a到b的长为 n 的路径，所以 R^*是所有Rⁿ的并集

R^* = R¹ U R²U…… U Rⁿ ( n次传递 )

传递性就是传递图关系中的连通性

引理1： 设A是含有n个元素的集合，R是集合A上的关系。如果R中存在一条从a到b的长度至少为1的路径，那么这两点间存在一条长度不超过n的路径。此外，当 a≠b 时，如果在R中存在一条从a到b的长度至少为1的路径，那么这两点间存在一条长度不超过n-1的路径。

2. 传递闭包的构造：

关系R的传递闭包等于连通性关系R^*

由引理1可知 R^*=R¹ U R² U …… U Rⁿ

设M_R是定义在n个元素集合上的关系R的0-1矩阵，那么传递闭包R_*的0-1矩阵：
M_R* = M_R v M_R ^[2] v …… v M_R ^[n]
（ M_R ^[x]是关系矩阵的x次乘积）