若积分区间相同,最常用的思想:
若
f
(
x
)
>
=
g
(
x
)
,
则
∫
a
b
f
(
x
)
>
=
∫
a
b
g
(
x
)
若f(x)>=g(x),则\int_{a}^{b}f(x)>=\int_{a}^{b}g(x)
若f(x)>=g(x),则∫abf(x)>=∫abg(x)
但
是
往
往
等
号
只
是
在
有
限
个
点
成
立
,
所
以
有
但是往往等号只是在有限个点成立,所以有
但是往往等号只是在有限个点成立,所以有
∫
a
b
f
(
x
)
>
∫
a
b
g
(
x
)
\int_{a}^{b}f(x)>\int_{a}^{b}g(x)
∫abf(x)>∫abg(x)
若区间关于原点对称,考虑奇偶性:
偶
倍
奇
零
偶倍奇零
偶倍奇零
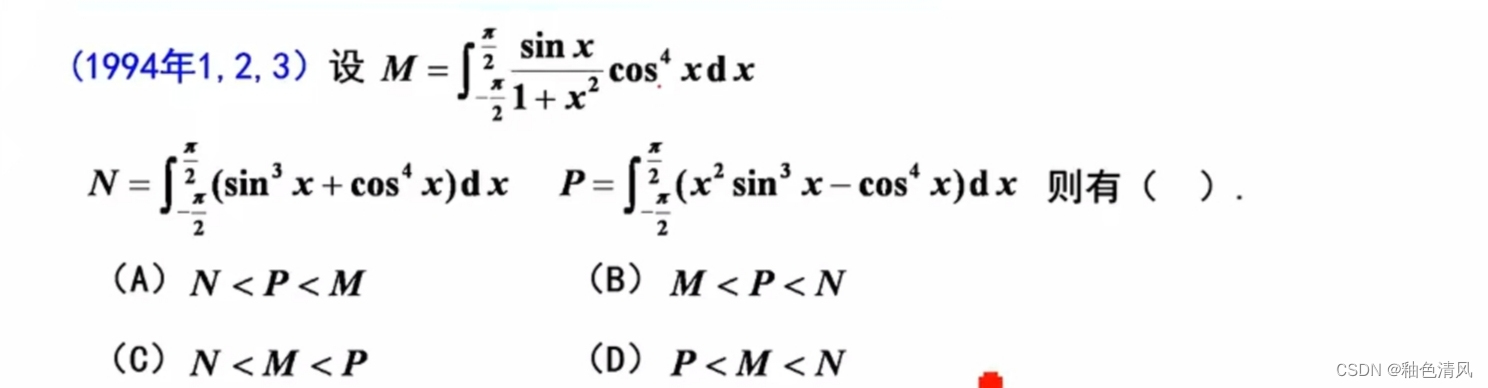

武忠祥老师每日一题||定积分基础训练(一)
news2026/2/9 2:44:15
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/485077.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Java实现添加文字水印、图片水印功能
Java实现添加水印功能 添加水印Java 2D API介绍绘制文字水印绘制图片水印循环添加文字水印 添加水印 为图片添加水印的主要作用是保护图片版权,防止图片被未经授权的人使用或传播。为图片添加水印是一种常用的图片处理技术。在Java 中可以使用JDK自带的 Graphics2D …
快速上手Django(九) -Django下载文件、Django上传文件、Django实现excel导入导出
文章目录 快速上手Django(九) -django 上传文件request.FILES,下载文件一、Django下载文件1. Django下载文件方案和思路2. HttpResponse、StreamingHttpResponse和FileResponse区别和选择StreamingHttpResponse和FileResponse对象的对比和选择使用HttpResponse使用S…
浏览器安全之XSS跨站脚本
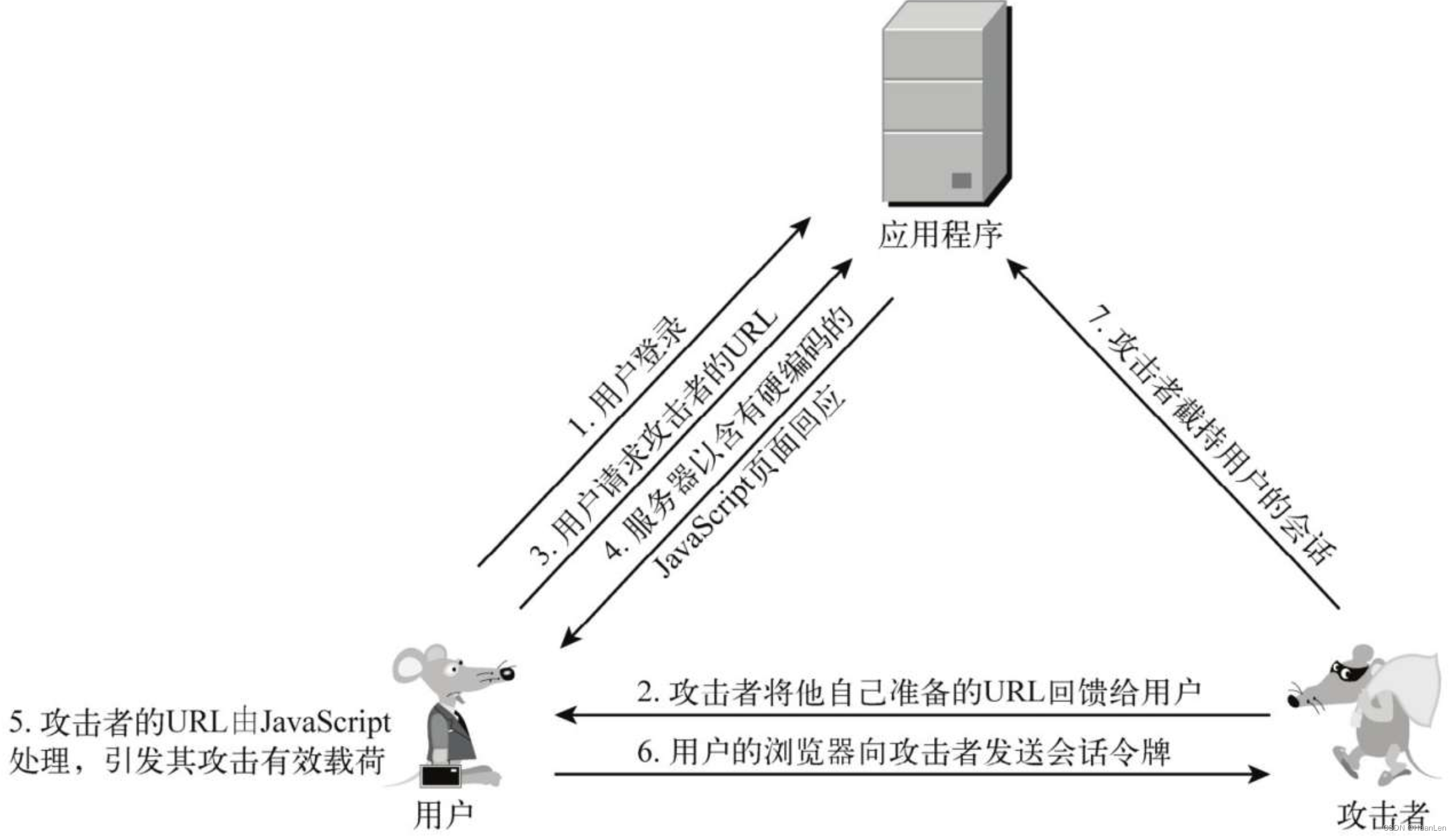
基本概念 跨站脚本(Cross-Site Scripting,XSS)是一种经常出现在Web应用程序中的计算机安全漏洞,是由于Web应用程序对用户的输入过滤不足而产生的。 攻击者利用网站漏洞把恶意的脚本代码(通常包括HTML代码和客户端Javas…
采用.Net Core技术框架开发的B/S版区域检验管理系统(云LIS)
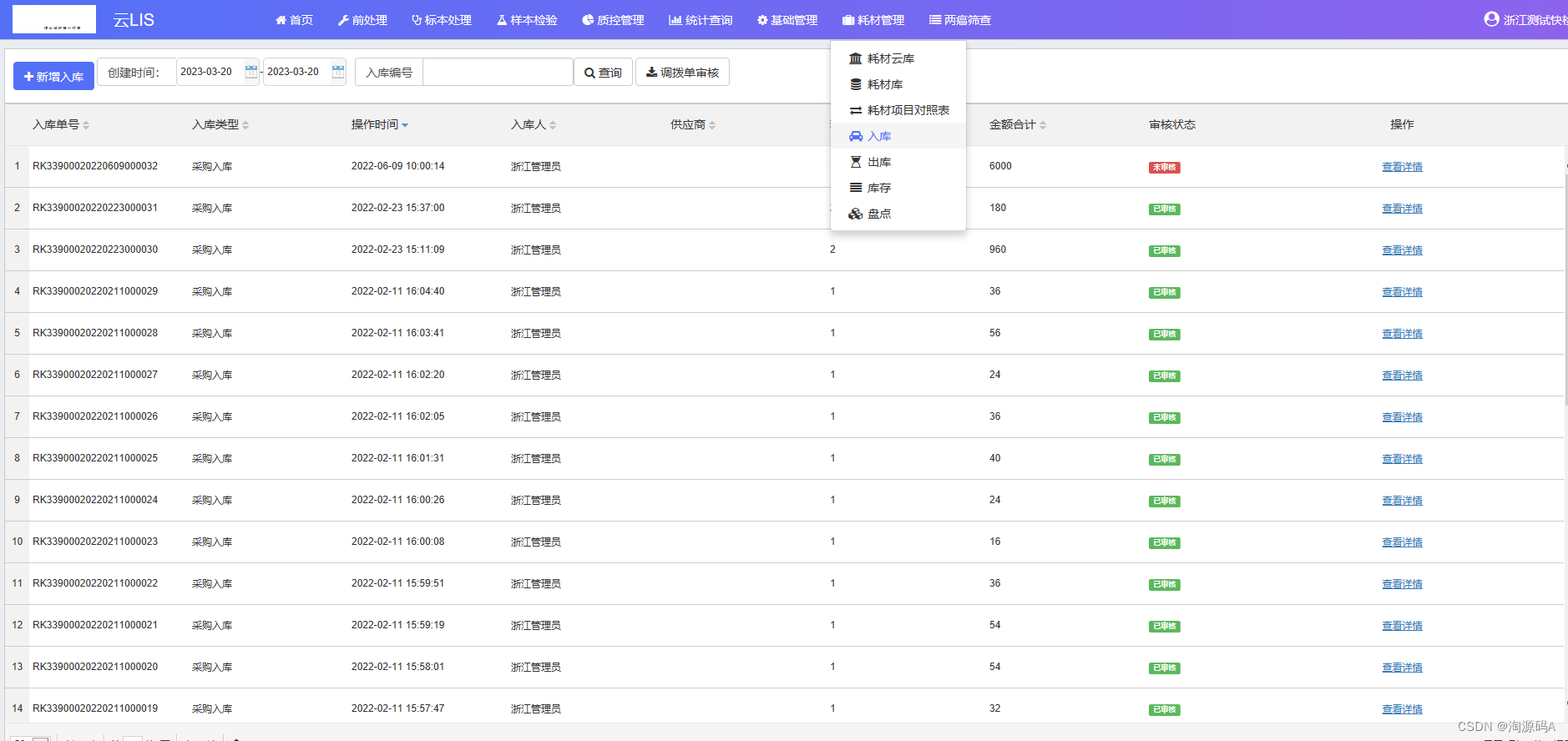
实验室信息管理系统云LIS源码 SaaS模式运维管理系统
云LIS系统源码是一款全面的实验室信息管理系统源码,其主要功能包括样本管理、检测项目管理、质控管理、报告管理、数据分析、两癌筛查等多个方面。具有独立的配套SaaS模式运维管理系统,支持远程运维&…
AtCoder Beginner Contest 300——A-G题讲解
蒟蒻来讲题,还望大家喜。若哪有问题,大家尽可提!
Hello, 大家好哇!本初中生蒟蒻讲解一下AtCoder Beginner Contest 300这场比赛的A-G题! A - N-choice question
原题
Problem Statement
Given integers A A A and…
基于改进的离散PSO算法的FJSP的研究(Python代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…
chatGPT免费入口-ChatGPT国内中文版网站
chatgpt怎么使用
如果您有Chat GPT的API Key并想要使用Chat GPT进行自然语言处理或生成处理,您可以按照以下步骤操作: 安装必要的软件和工具
在使用Chat GPT之前,您需要先安装一些必要的软件和工具,例如Python解释器、HTTP客户…
【Android车载系列】第11章 系统服务-SystemServer自定义服务
1 编写自定义系统服务
1.1 AIDL接口定义
系统源码目录/frameworks/base/core/java/android/app/下新建AIDL接口IYvanManager.aidl
package android.app;/**
* 目录:/frameworks/base/core/java/android/app/IYvanManager.aidl
*/
interface IYvanManager{String …
YOLOV5入门讲解+常用数据集
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…
TIM-输出比较(PWM)——STM32
TIM-输出比较——STM32
Oc (Output Compare) 输出比较 输出比较可以通过比较CNT与CCR寄存器值的关系,来对输出电平进行置1、置0或翻转的操作,用于输出一定频率和占空比的PWM波形 每个高级定时器和通用定时器都拥有4个输出比较通道高级定时器的前3个通道…
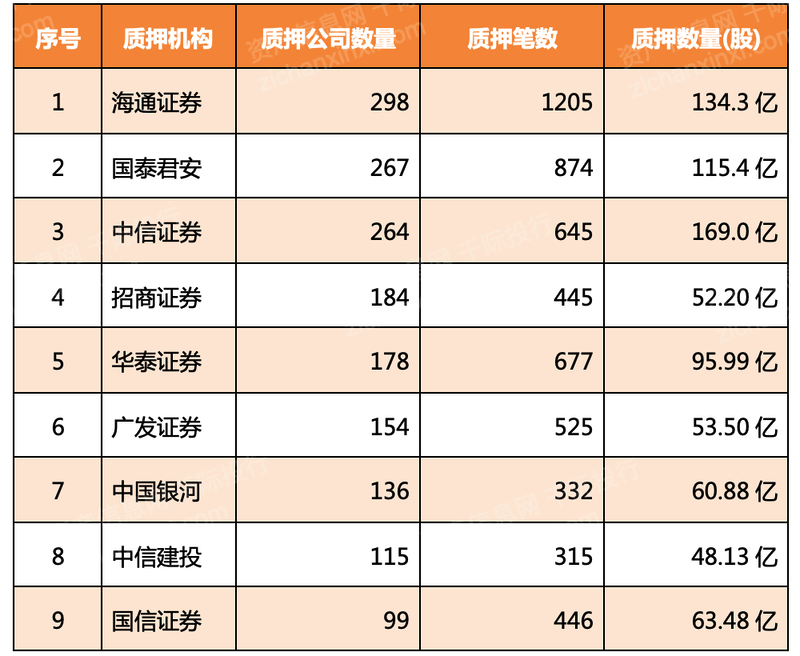
2023年股票质押违约处置研究报告
第一章 行业概况
1.1 产品定义
股票质押违约处置是指在股票质押融资中,当质押人(股票持有者)无法按照约定履行还款义务时,质权人(通常为金融机构)对质押股票进行处置的一系列活动。这个行业涉及到多个领域…
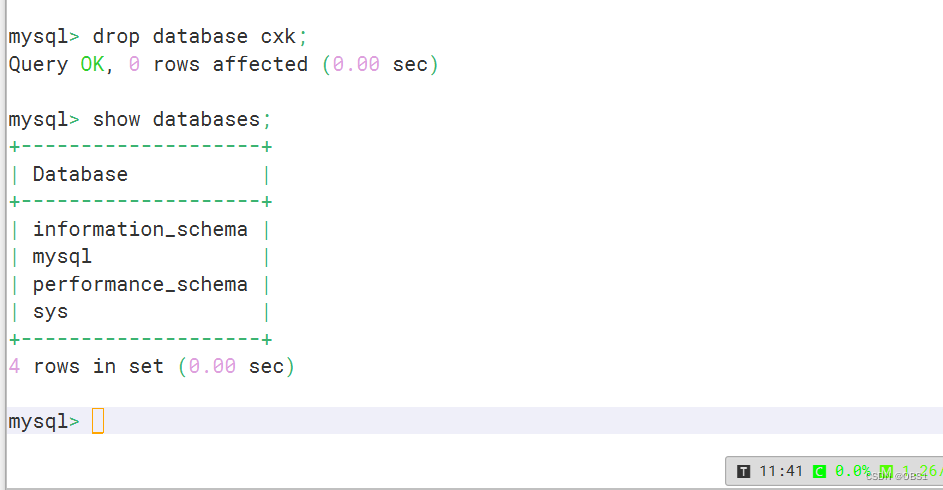
DAY 55 mysql数据库管理
常用的数据类型:
类型说明int整型,用于定义整数类型的数据fload单精度浮点4字节32位,准确表示到小数点后六位double双精度浮点8字节64位char固定长度的字符类型,用于定义字符类型数据。varchar可变长度的字符类型text文本image图…
Python基础合集 练习23 (错误与异常语句处理3)
‘’’ raise语句 raise[ExceptionName[(reason)]] 其中ExceptionName[(reason)]是可选参数用来指定抛出异常名称和原因,如果省略该参数,就会原样输出当前的错误 ‘’’
在下面程序中,使用raise语句抛出ValueError异常
def num_calu(): book int(input(输入图书数量: )) stu…
探秘C语言:位运算符的奥秘
本篇博客会讲解C语言中的6个位操作符:按位取反(~)、按位与(&)、按位或(|)、按位异或(^)、左移(<<)、右移(>>)。这6个操作符都是操作整数的二进制位的。在学习这6个位操作符之前,大家需要先掌握“整数在内存中的存储”这个知识点…
数电中需要注意的问题
逻辑函数表达式之间的相互转换 (更多请详见PPT)若题目要求用: 与非门实现逻辑函数,则画卡诺图圈出值为1的然后化简 或非门实现逻辑函数,则画卡诺图圈出值为0的然后化简 与或非门实现逻辑函数,则画卡诺图圈…
一文了解获得 Zebec Labs 投资的 Coral Finance,空投计划或在不久推出
在前不久,Zebec Labs宣布对链上衍生品协议Coral Finance进行150万美元的投资,以帮助该协议完成早期启动并,并在后续持续的为其提供孵化支持。Coral Finance将在不久部署在Nautilus Chain主网上。据了解,Coral Finance是Nautilus C…
博客系统的后端设计(一) - 准备工作与设计数据库
文章目录 准备工作1. 创建一个 Maven 项目2. 引入依赖3. 创建目录结构 设计数据库 这次开始进行博客系统后端的进度,本篇博客讲的是
准备工作和
设计数据库两个步骤。 准备工作
1. 创建一个 Maven 项目 2. 引入依赖 在地址栏中搜素 https://mvnrepository.com/&a…