第一题

问题分析

从收货量、发货量、快递数量增长/减少趋势、相关性等多角度考虑，建立数学模型，对各站点城市的重要程度进行综合排序

用脚丫子想，收货量大、发货量大、快递数量呈现增长趋势、链出的城市多，城市就重要。

如何建模？可以参考谷歌网页排名算法 pagerank，通过对网页之间的链接结构和链接权重分析网页重要性。

附件 1 数据中，快递的路径取值如下：
‘A->O’, ‘S->R’, ‘S->Q’, ‘S->L’, ‘S->I’, ‘S->D’, ‘R->S’, ‘R->O’, ‘R->L’, ‘R->G’, ‘R->D’, ‘Q->V’, ‘Q->M’, ‘Q->A’, ‘P->D’, ‘O->R’, ‘O->Q’, ‘O->G’, ‘T->X’, ‘N->V’, ‘U->A’, ‘U->O’, ‘Y->X’, ‘Y->W’, ‘Y->L’, ‘X->Y’, ‘X->W’, ‘X->L’, ‘X->G’, ‘W->Y’, ‘W->X’, ‘W->L’, ‘V->Q’, ‘V->N’, ‘V->M’, ‘V->G’, ‘V->C’, ‘V->A’, ‘U->V’, ‘U->G’, ‘N->M’, ‘T->B’, ‘M->V’, ‘G->X’, ‘G->V’, ‘G->R’, ‘G->Q’, ‘G->O’, ‘G->N’, ‘G->L’, ‘E->I’, ‘D->R’, ‘D->E’, ‘D->A’, ‘C->V’, ‘C->U’, ‘C->N’, ‘C->M’, ‘B->G’, ‘N->G’, ‘I->E’, ‘I->J’, ‘A->Q’, ‘J->I’, ‘I->S’, ‘M->N’, ‘M->G’, ‘M->C’, ‘L->X’, ‘L->W’, ‘L->R’, ‘L->P’, ‘L->O’, ‘M->U’, ‘L->J’, ‘L->G’, ‘L->D’, ‘K->L’, ‘K->J’, ‘J->L’, ‘J->K’, ‘L->K’, ‘Q->O’, ‘D->L’, ‘Q->N’, ‘H->J’, ‘H->K’, ‘H->L’, ‘J->H’, ‘L->H’, ‘K->H’

绘制有向图：

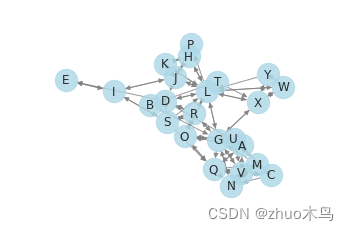
PageRank 算法（可跳过）

PageRank 算法将互联网看作一个有向图，每个网页看作图中的一个节点，每个链接看作图中的一条边，网页之间的链接关系构成了整个图的拓扑结构。在这个图中，PageRank 算法将网页的重要性定义为所有指向该网页的链接节点 PageRank 值的加权平均值。即一个网页的重要性等于它所链接的所有网页的重要性之和，这些网页的重要性需要按照它们自身的 PageRank 值进行加权。

PageRank 算法将网页的重要性定义为一个网页被其他重要网页链接的数量和质量的加权平均值。具体来说，网页 A 的 PageRank 值可以用以下公式计算：
$$PR(A)=\frac{1-d}{N}+d\cdot \sum _{i\in B_A}\frac{PR(i)}{L(i)}$$

其中，$PR(A)$ 表示网页 A 的 PageRank 值，$N$ 表示网页总数，$d$ 是一个介于 0 和 1 之间的阻尼系数（也称为跳转概率，通常取值为 0.85），$B_A$ 表示所有指向网页 A 的网页集合，$L(i)$ 表示网页 i 的出度（即指向其他网页的链接数）。

公式的意义是：网页 A 的 PageRank 值等于一个固定的基础值 $\frac{1-d}{N}$ 加上所有指向网页 A 的其他网页的 PageRank 值的加权平均值。其中，权重取决于链接网页的出度（出度越大，权重越小）和这些链接网页的 PageRank 值（PageRank 值越高，权重越大），同时还要乘以阻尼系数 d。

PageRank 算法修正

PageRank 算法的核心思想是基于以下两个假设：

1. 如果一个网页被很多其他网页链接到，那么它很可能是一个重要的网页。
2. 如果一个网页链接到很多其他网页，那么它很可能是一个不太重要的网页。

要用于解决问题一，套用 pagerank 肯定不行。因为链出城市越多，这个城市越重要才对，因此修正如下：
$$PR(A)=\frac{1-d}{N}+d\cdot \sum _{i\in B_A}PR(i)\cdot \frac{L(i)}{N}$$
除法该惩罚，简单粗暴。

此外，每一个链出，应赋予权重，这个权重表示收货量、发货量、快递量增长。为此，将上式引入权重，修正为：
$$PR(A)=\frac{1-d}{N}+d\cdot \sum _{i\in B_A}PR(i)\cdot \frac{L(i)}{N}\cdot w_{i->A}$$
其中，$w_{i->A}$为 i 链到 A 的权重

权重系数

那么权重如何求？
我们手头上有 2018-04-19 至 2019-04-17 的快递量数据（路径已经包含了收发信息），针对每一月进行 Zscore 标准化，得到“快递量（局部标准化）”。然后对所有数据进行 Zscore 标准化，得到 “快递量（全局标准化）”。

局部标准化中，每一天的快递量与本月做对比。全局快递量与一年作对比。前者没有考虑月度增长，能够静态反映所有路径快递量的情况。后者考虑增长，动态反映了所有路径的快递量情况。

增长率的考虑应引入一元线性回归，然后取他的斜率和相关系数。

一元线性回归的数学原理基于统计学中的线性回归模型，假设响应变量 y 和一个或多个解释变量 x 之间存在线性关系，即

y = a * x + b + e

其中，a 为斜率，b 为截距，e 为随机误差。通过最小二乘法，我们可以得到 a 和 b 的估计值，以及其他统计信息，如 t 值、p 值、标准误差和相关系数等。

相关系数（r）是表示两个变量之间关系的一种统计量，其取值范围在 -1 和 1 之间。当 r=1 时，表示两个变量之间存在完全正向线性关系；当 r=-1 时，表示两个变量之间存在完全负向线性关系；当 r=0 时，表示两个变量之间不存在线性关系。

于是表示增长率权重系数为：将斜率和 r 进行最大最小值标准化后，用 $a\times r$ 表示。

同样，对快递数（全局）、快递数（局部）进行最大最小值标准化，然后得到权重公式：
$$w=[快递数（全局）+快递数（局部）+a\times r]/3$$

最终可得：

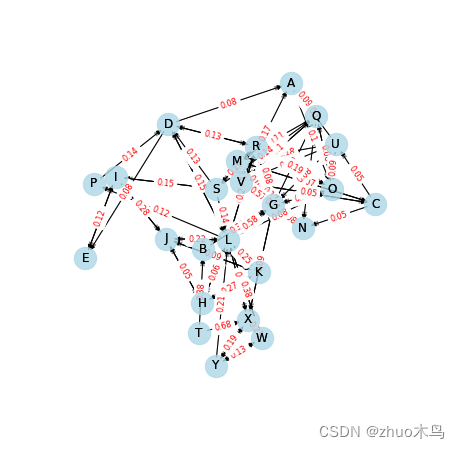
结果

各城市链出与链入

链出 + 权重

A -> [(‘O’, 0.1), (‘Q’, 0.14)]
B -> [(‘G’, 0.38)]
C -> [(‘M’, 0.06), (‘N’, 0.05), (‘U’, 0.05), (‘V’, 0.06)]
D -> [(‘A’, 0.08), (‘E’, 0.08), (‘L’, 0.08), (‘R’, 0.08)]
E -> [(‘I’, 0.19)]
G -> [(‘L’, 0.61), (‘N’, 0.06), (‘O’, 0.27), (‘Q’, 0.1), (‘R’, 0.13), (‘V’, 0.72), (‘X’, 0.08)]
H -> [(‘J’, 0.33), (‘K’, 0.08), (‘L’, 0.06)]
I -> [(‘E’, 0.12), (‘J’, 0.25), (‘S’, 0.1)]
J -> [(‘H’, 0.05), (‘I’, 0.28), (‘K’, 0.27), (‘L’, 0.22)]
K -> [(‘H’, 0.27), (‘J’, 0.09), (‘L’, 0.25)]
L -> [(‘D’, 0.15), (‘G’, 0.58), (‘H’, 0.18), (‘J’, 0.27), (‘K’, 0.21), (‘O’, 0.08), (‘P’, 0.12), (‘R’, 0.19), (‘W’, 0.41), (‘X’, 0.15)]
M -> [(‘C’, 0.07), (‘G’, 0.08), (‘N’, 0.11), (‘U’, 0.18), (‘V’, 0.11)]
N -> [(‘G’, 0.08), (‘M’, 0.17), (‘V’, 0.17)]
O -> [(‘G’, 0.2), (‘Q’, 0.21), (‘R’, 0.16)]
P -> [(‘D’, 0.14)]
Q -> [(‘A’, 0.09), (‘M’, 0.11), (‘N’, 0.11), (‘O’, 0.08), (‘V’, 0.08)]
R -> [(‘D’, 0.13), (‘G’, 0.08), (‘L’, 0.2), (‘O’, 0.19), (‘S’, 0.3)]
S -> [(‘D’, 0.13), (‘I’, 0.15), (‘L’, 0.14), (‘Q’, 0.14), (‘R’, 0.19)]
T -> [(‘B’, 0.38), (‘X’, 0.68)]
U -> [(‘A’, 0.1), (‘G’, 0.08), (‘O’, 0.09), (‘V’, 0.13)]
V -> [(‘A’, 0.17), (‘C’, 0.05), (‘G’, 0.57), (‘M’, 0.11), (‘N’, 0.11), (‘Q’, 0.1)]
W -> [(‘L’, 0.38), (‘X’, 0.21), (‘Y’, 0.13)]
X -> [(‘G’, 0.09), (‘L’, 0.21), (‘W’, 0.23), (‘Y’, 0.23)]
Y -> [(‘L’, 0.21), (‘W’, 0.13), (‘X’, 0.19)]

链入 + 权重

O <- [(‘A’, 0.1), (‘G’, 0.27), (‘L’, 0.08), (‘Q’, 0.08), (‘R’, 0.19), (‘U’, 0.09)]
Q <- [(‘A’, 0.14), (‘G’, 0.1), (‘O’, 0.21), (‘S’, 0.14), (‘V’, 0.1)]
G <- [(‘B’, 0.38), (‘L’, 0.58), (‘M’, 0.08), (‘N’, 0.08), (‘O’, 0.2), (‘R’, 0.08), (‘U’, 0.08), (‘V’, 0.57), (‘X’, 0.09)]
M <- [(‘C’, 0.06), (‘N’, 0.17), (‘Q’, 0.11), (‘V’, 0.11)]
N <- [(‘C’, 0.05), (‘G’, 0.06), (‘M’, 0.11), (‘Q’, 0.11), (‘V’, 0.11)]
U <- [(‘C’, 0.05), (‘M’, 0.18)]
V <- [(‘C’, 0.06), (‘G’, 0.72), (‘M’, 0.11), (‘N’, 0.17), (‘Q’, 0.08), (‘U’, 0.13)]
A <- [(‘D’, 0.08), (‘Q’, 0.09), (‘U’, 0.1), (‘V’, 0.17)]
E <- [(‘D’, 0.08), (‘I’, 0.12)]
L <- [(‘D’, 0.08), (‘G’, 0.61), (‘H’, 0.06), (‘J’, 0.22), (‘K’, 0.25), (‘R’, 0.2), (‘S’, 0.14), (‘W’, 0.38), (‘X’, 0.21), (‘Y’, 0.21)]
R <- [(‘D’, 0.08), (‘G’, 0.13), (‘L’, 0.19), (‘O’, 0.16), (‘S’, 0.19)]
I <- [(‘E’, 0.19), (‘J’, 0.28), (‘S’, 0.15)]
X <- [(‘G’, 0.08), (‘L’, 0.15), (‘T’, 0.68), (‘W’, 0.21), (‘Y’, 0.19)]
J <- [(‘H’, 0.33), (‘I’, 0.25), (‘K’, 0.09), (‘L’, 0.27)]
K <- [(‘H’, 0.08), (‘J’, 0.27), (‘L’, 0.21)]
S <- [(‘I’, 0.1), (‘R’, 0.3)]
H <- [(‘J’, 0.05), (‘K’, 0.27), (‘L’, 0.18)]
D <- [(‘L’, 0.15), (‘P’, 0.14), (‘R’, 0.13), (‘S’, 0.13)]
P <- [(‘L’, 0.12)]
W <- [(‘L’, 0.41), (‘X’, 0.23), (‘Y’, 0.13)]
C <- [(‘M’, 0.07), (‘V’, 0.05)]
B <- [(‘T’, 0.38)]
Y <- [(‘W’, 0.13), (‘X’, 0.23)]

PageRank 算法结果

最终结果，G、L、V、W、O 最重要！可以从链出、链入和权重中亦可以发现

达到精度, 迭代终止，迭代次数为： 11
城市 G 的 PageRank 值为 0.00682
城市 L 的 PageRank 值为 0.00648
城市 V 的 PageRank 值为 0.00584
城市 W 的 PageRank 值为 0.00539
城市 O 的 PageRank 值为 0.00519
城市 R 的 PageRank 值为 0.00519
城市 J 的 PageRank 值为 0.00518
城市 X 的 PageRank 值为 0.0051
城市 K 的 PageRank 值为 0.00493
城市 D 的 PageRank 值为 0.00479
城市 H 的 PageRank 值为 0.00478
城市 Q 的 PageRank 值为 0.00477
城市 N 的 PageRank 值为 0.00463
城市 A 的 PageRank 值为 0.00459
城市 I 的 PageRank 值为 0.00454
城市 M 的 PageRank 值为 0.00454
城市 S 的 PageRank 值为 0.00451
城市 P 的 PageRank 值为 0.00447
城市 Y 的 PageRank 值为 0.00442
城市 U 的 PageRank 值为 0.00436
城市 C 的 PageRank 值为 0.0043
城市 B 的 PageRank 值为 0.00429
城市 E 的 PageRank 值为 0.00429
城市 T 的 PageRank 值为 0.00417

代码

代码文章链接：2023 年 五一杯 B 题第一问代码