专有名词解释：

决策树：决策树是根据已知若干条件，来对事件做出判断。从根节点到叶子结点。自上而下生成，每个决策或事件都可能引发两个或多个事件。将这些事件根据不同的特征进行划分，最后将类别分出，得到决策结果。

实例讲解（重点理解以实现算法）：

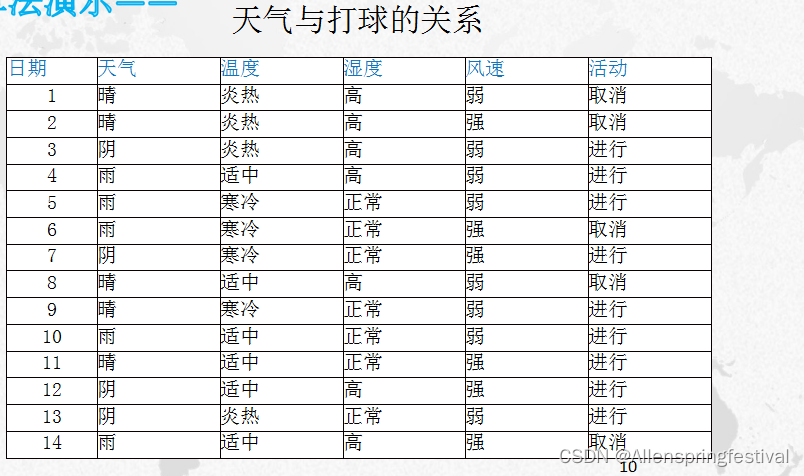
5个取消，9个进行

 先算出来活动entropy值（信息熵）：

接着突出天气状况的条件熵：

 即在天气是晴，阴，雨下决策时进行还是取消的条件概率。（先分类再去求信息熵）

其余同理：

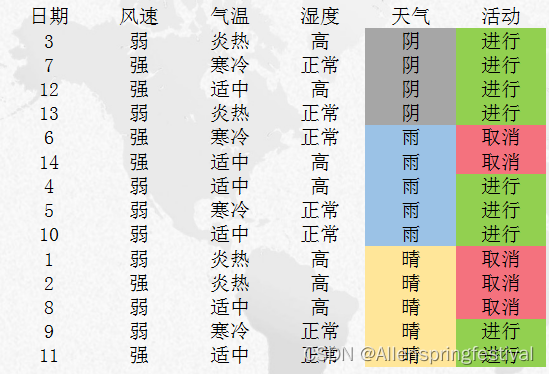
 counting:

 接着用活动的信息熵去减去条件熵得到各信息熵增益：

 选择熵增益最大的天气属性列进行分类：

在天气为阴的时候，得到的结果全是进行，而在晴和雨的时候不确定；

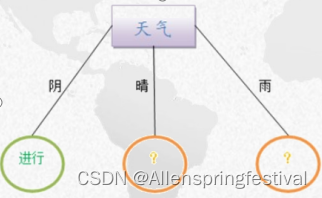
 进行下一步决策树分类：查找下一个熵增益最大的属性列

当天气属性列为晴的时候：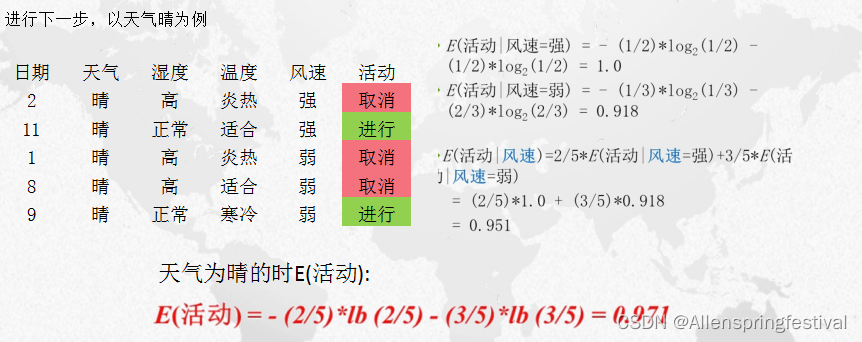

 其他同理：

 在天气为晴的条件下(不确定）的各信息增益：

可以得到

湿度的信息增益是最高的，由此以湿度作为树节点（活动跟这个属性列越关联）

同理由于天气为雨的时候也是·不确定，所以我们经过同样的过程可以得到风速的属性列的信息增益是最高的。

这样就得到了决策树及其关联规则：

 ID3算法的优缺点：

算法展示：

(1)数据加载

 数据加载函数，用来读取数据集并进行简单处理

(2)计算信息熵

num_label = len(df[label].unique)  #在固定的类别属性下，标签属性有几个

y=len(df)    #在固定的类别属性下，有几行数据

来根据实例进行理解：  

下面就可以计算每个类别属性的信息增益：

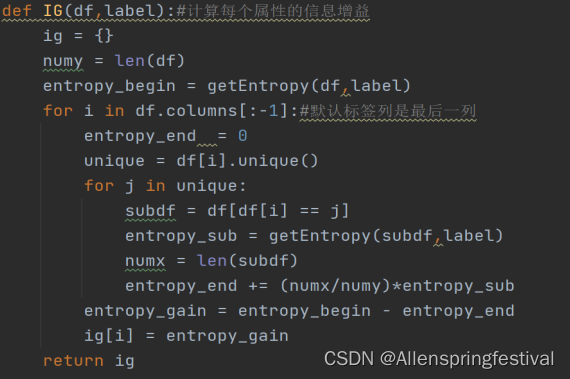
接着找到频率最高的决策属性值：获取最佳分裂点。

 

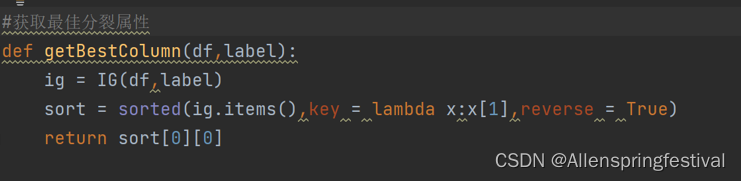
下面就可以构建决策树：

的

def getTree（df,label.tree）:

#df：训练集，label：决策属性，tree：决策树

if len(df[label].unique())==1：

        tree=df[label].unique()[0]

        return tree

#如果所有数据都在一个标签属性下，则递归停止，返回该标签。

elif len(df.columns)==1:#就一个属性列决定标签列

        tree=df[df.columns[-1]].value_counts().max()

        return tree

#递归停止，返回数目最多的那个类别

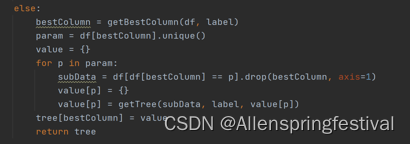
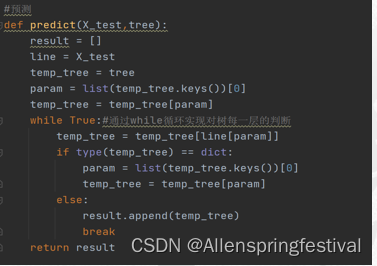
#根据分裂属性的值划分子树