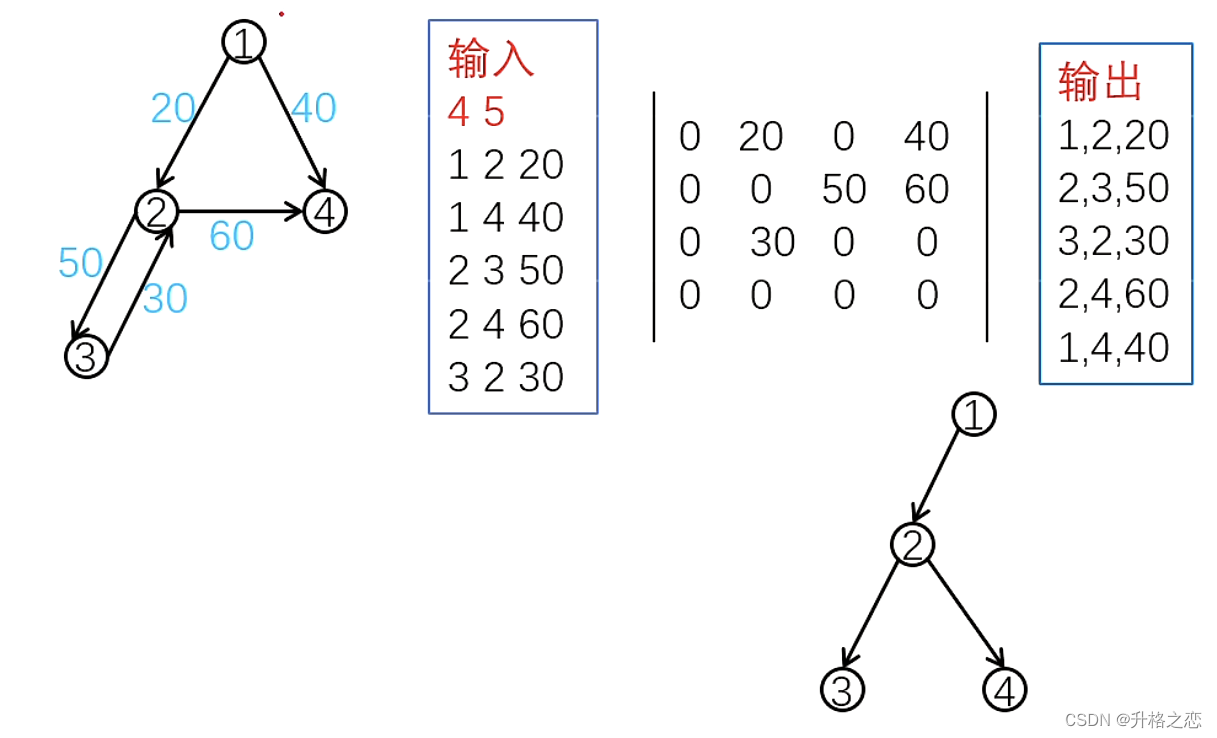
邻接矩阵

使用二维数组w[u][v]存储点u到点v的边的权值。一般应用在点数不多的稠密图
时间复杂度：O(n²)
空间复杂度：O(n²)

int w[N][N];		// edge
int vis[N];			// visited

void dfs(int u){
	vis[u] = true;
	for(int v = 1; v <= n; ++ v)
		if(w[u][v]){
			printf(%d, %d, %d\n", u,v,w[u][v]);
			if(vis[v]) continue;		// 防止重复访问
			dfs(v);
		}
}

int main(){
	cin >> n >> m;
	for(int i = 1; i <= m; ++ i){
		cin >> a >> b >> c;
		w[a][b] = c;
		w[b][a] = c;			// 无向图
	}
	dfs(1);
	return 0;
}

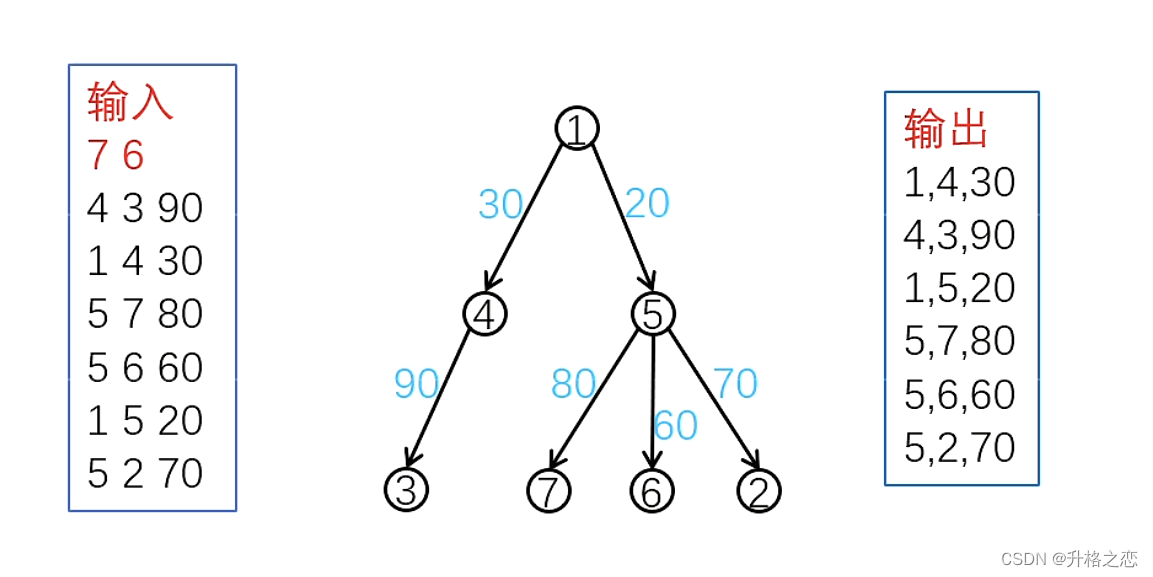
边集数组

边集数组e[i]存储第i条边的「起点、终点、边权」。在kruskal算法中，将边按边权排序，直接存边。
时间复杂度：O(nm)
空间复杂度：O(m)

struct edge{
	int u, v, w;
}e[M];
int vis[N];

void dfs(int u){
	vis[u] = true;
	for(int i = 1; i <= m; ++ i){		// 不知道节点后边有多少边。暴力枚举m次。
		if(e[i].u == u){				// 枚举以u做起点的边
			int v = e[i].v, w = e[i].w;
			printf(%d, %d, %d\n", u,v,w[u][v]);
			if(vis[v]) continue;
			dfs(e[i].v);
		}
}

int main(){
	cin >> n >> m;
	for(int i = 1; i <= m; ++ i){
		cin >> a >> b >> c;
		e[i] = {a, b, c};
		// e[i] = {b, a, c};	// 无向图
	}
	dfs(1);
	return 0;
}

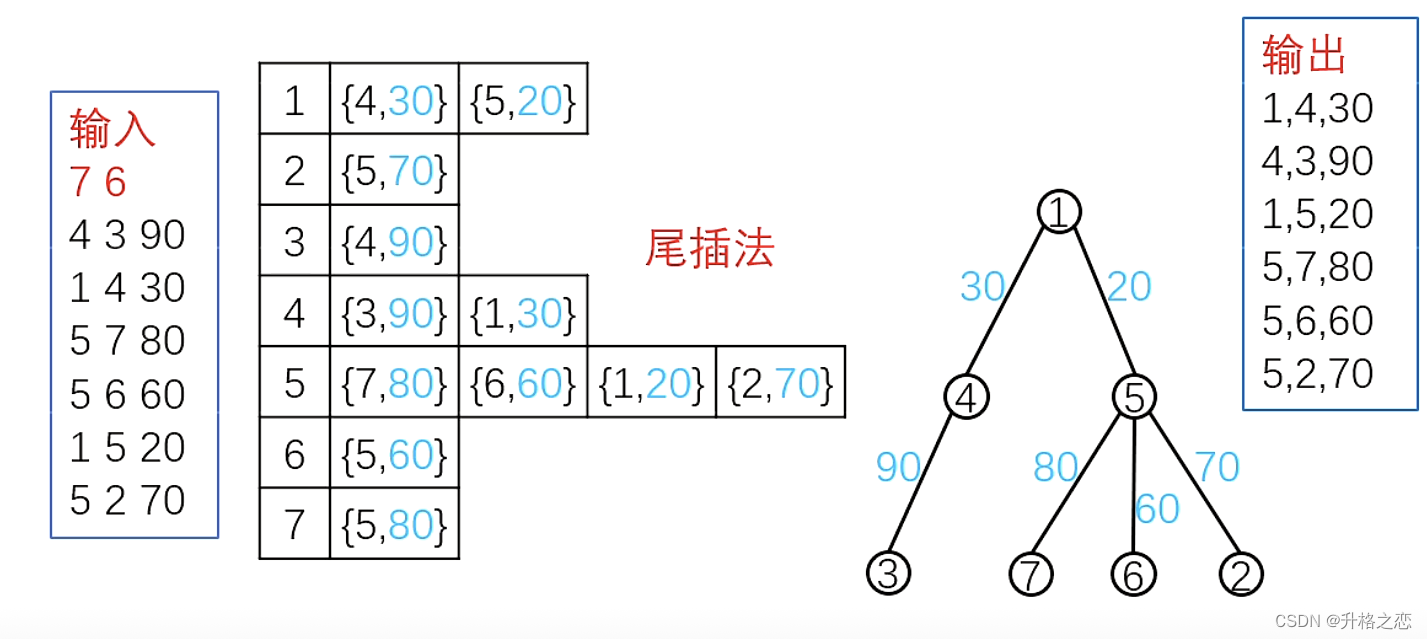
邻接表

出边数组e[u][i]存储u的所有出边「终点v，边权w」。可以处理各种图，不能处理反向边。效率最高。
时间复杂度：O(n+m)
空间复杂度：O(n+m)

struct edge{int v, w};
vector<edge> e[N];		// 

void dfs(int u, int fa){
	for(auto ed : e[u]){
		int v = ed.v, w = ed.w;
		if(v == fa) continue;			// 终点等于父节点，防止循环访问
		printf(%d, %d, %d\n", u,v,w);
		dfs(v, u);
	}
}

int main(){
	cin >> n >> m;
	for(int i = 1; i <= m; ++ i){
		cin >> a >> b >> c;
		e[a].push_back({b, c});
		e[b].push_back({a, c});
	}
	dfs(1, 0);			// 假设1号节点的父节点是0
	return 0;
}

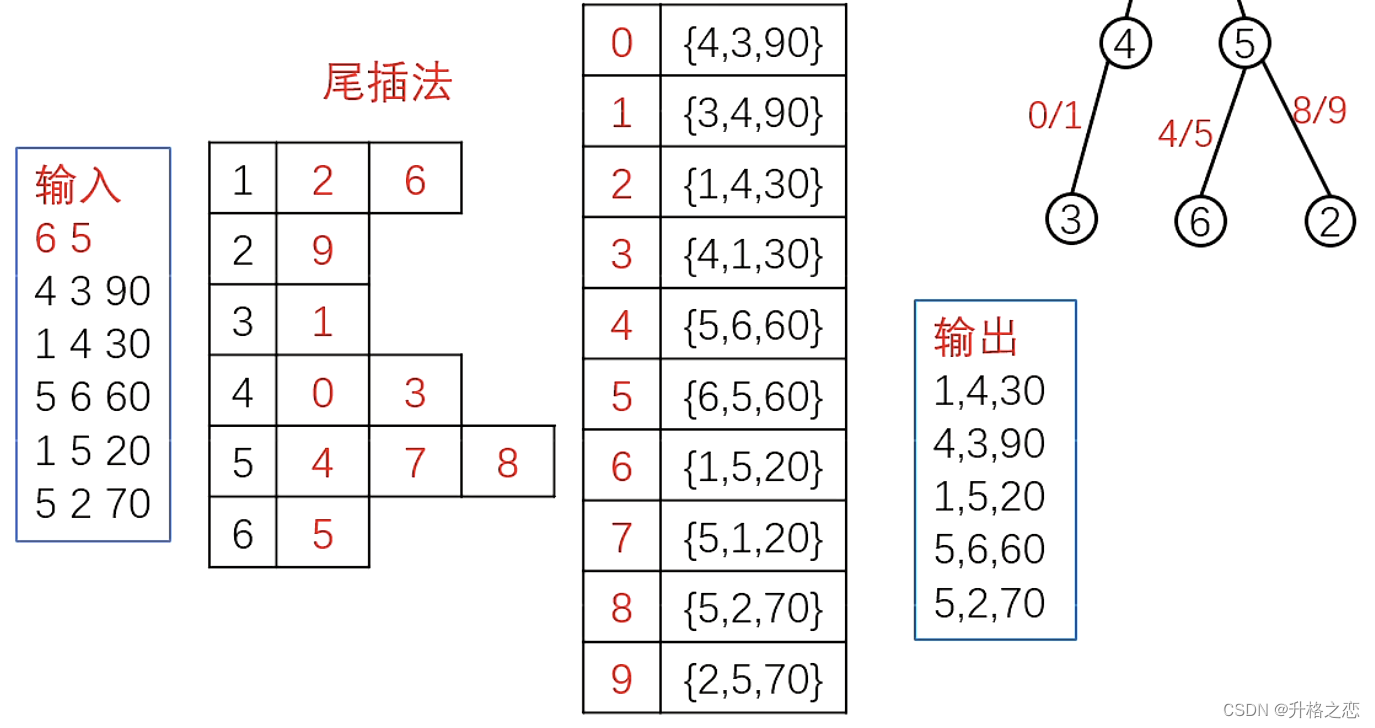
链式邻接表

边集数组e[j]存储第j条边的「起点u、终点v、边权w」。能处理反向边
表头数组h[u][i]存储u点的所有出边的编号
时间复杂度：O(n+m)
空间复杂度：O(n+m)

struct edge{int u, v, w};
vector<edge> e;			// 
vector<int> h[N];		// 点的所有出边

void add(int a, int b, int c){
	e.push_back({a, b, c});
	h[a].push_back(e.size() - 1);		// h记录该编号节点的所有出边的编号
}

void dfs(int u, int fa){
	for(int i = 0; i < h[u].size(); ++ i){ // u为起点的编号
		int j = h[u][i];				// j为终点的编号
		int v = e[j].v, w = e[j].w;
		if(v == fa) continue;			// 终点等于父节点
		printf(%d, %d, %d\n", u,v,w);
		dfs(v, u);
	}
}

int main(){
	cin >> n >> m;
	for(int i = 1; i <= m; ++ i){
		cin >> a >> b >> c;
		add(b, c);
		add(a, c);
	}
	dfs(1, 0);			// 假设1号节点的父节点是0
	return 0;
}

链式前向星

一个表头数组悬挂多个链表
边集数组e[i]存储第i条出边的「终点v、边权w、下一条边ne」
表头数组h[u]存储u点的第一条出边的编号
边的编号idx可取0，1，2，3

时间复杂度：O(n+m)
空间复杂度：O(n+m)

struct edge{int v, w, ne};	// 终点、边权、下一条边编号
edge e[M];				// 边集
int idx, h[N];			// 第一条出边

void add(int a, int b, int c){
	e[idx] = {b, c, h[a]};	// 每个点后加的第一条边的h值一定是-1
	h[a] = idx++;		// idx记录边的编号，没加一条边就增加1。头插法，先插后访问。
}

void dfs(int u, int fa){
	// -1取反为0
	for(int i = h[u]; ~ i; i = e[i].ne){ // u为起点的编号，h[u]就是u节点第一条出边编号
		int v = e[i].v, w = e[i].w;
		if(v == fa) continue;			// 终点等于父节点
		printf(%d, %d, %d\n", u,v,w);
		dfs(v, u);
	}
}

int main(){
	cin >> n >> m;
	memset(h, -1, sizeof h);		// 表头初始化为-1，遍历到-1说明结束
	for(int i = 1; i <= m; ++ i){
		cin >> a >> b >> c;
		add(a, b, c);
		add(b, a, c);
	}
	dfs(1, 0);			// 假设1号节点的父节点是0
	return 0;
}