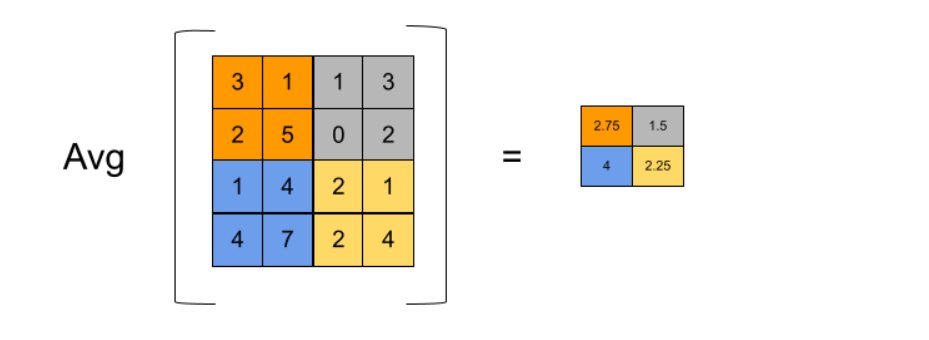
二维平均池层计算损失相对于其输入张量的梯度，方法是将损失相对于输出张量的梯度均分在输入子区域，这些子区域在前向传播中被用来计算平均值。

由于平均集合计算的是每个输入子区域的平均值，所以子区域中的每个元素对平均值的贡献是相同的。因此，在反向传播过程中，与子区域中每个元素有关的损失梯度等于与相应的输出元素有关的损失梯度除以子区域的大小。

import torch
import torch.nn as nn

avg_pool = nn.AvgPool2d(kernel_size=(2, 2), stride=(2, 2))

x = torch.randn(1, 1, 4, 4, requires_grad=True)
y = avg_pool(x)

# Compute some loss
loss = y.sum()
print(loss) # tensor(-0.1558, grad_fn=<SumBackward0>)

# Compute gradients
loss.backward()

# Check gradients
print(x.grad)
# tensor([[[[ 0.0625,  0.0625, -0.1875, -0.1875],
#           [ 0.0625,  0.0625, -0.1875, -0.1875],
#           [-0.1250, -0.1250, -0.0625, -0.0625],
#           [-0.1250, -0.1250, -0.0625, -0.0625]]]])

结果就是：

tensor([[[[0.2500, 0.2500, 0.2500, 0.2500],
          [0.2500, 0.2500, 0.2500, 0.2500],
          [0.2500, 0.2500, 0.2500, 0.2500],
          [0.2500, 0.2500, 0.2500, 0.2500]]]])

解读：

在这个例子中，创建了一个具有kernel_size=(2 ,2) and stride=(2 ,2)的AvgPool2d层。一个形状为(1 ,1 ,4 ,4)且require_grad=True的输入张量x通过该层，产生一个形状为(1 ,1 ,2 ,2)的输出张量y。

损失被计算为y中所有元素之和，其值为-0.1558。在反向传播过程中，损失相对于x的梯度是通过将损失相对于y的梯度分布在用于计算y的平均值的(2,2)输入子区域来计算的。

在这种情况下，由于y中有四个输出元素，它们的梯度是[1 ,1 ,1 ,1]。这些梯度分布在各自的(2 ,2)输入子区域，子区域的每个元素得到的梯度等于其对应的输出元素的梯度除以(2 * 2) = 4。因此，x.grad中的元素的值为[1/4 ,1/4 ,1/4 ,1/4]。