高级数据结构专题

news2025/1/11 20:58:41

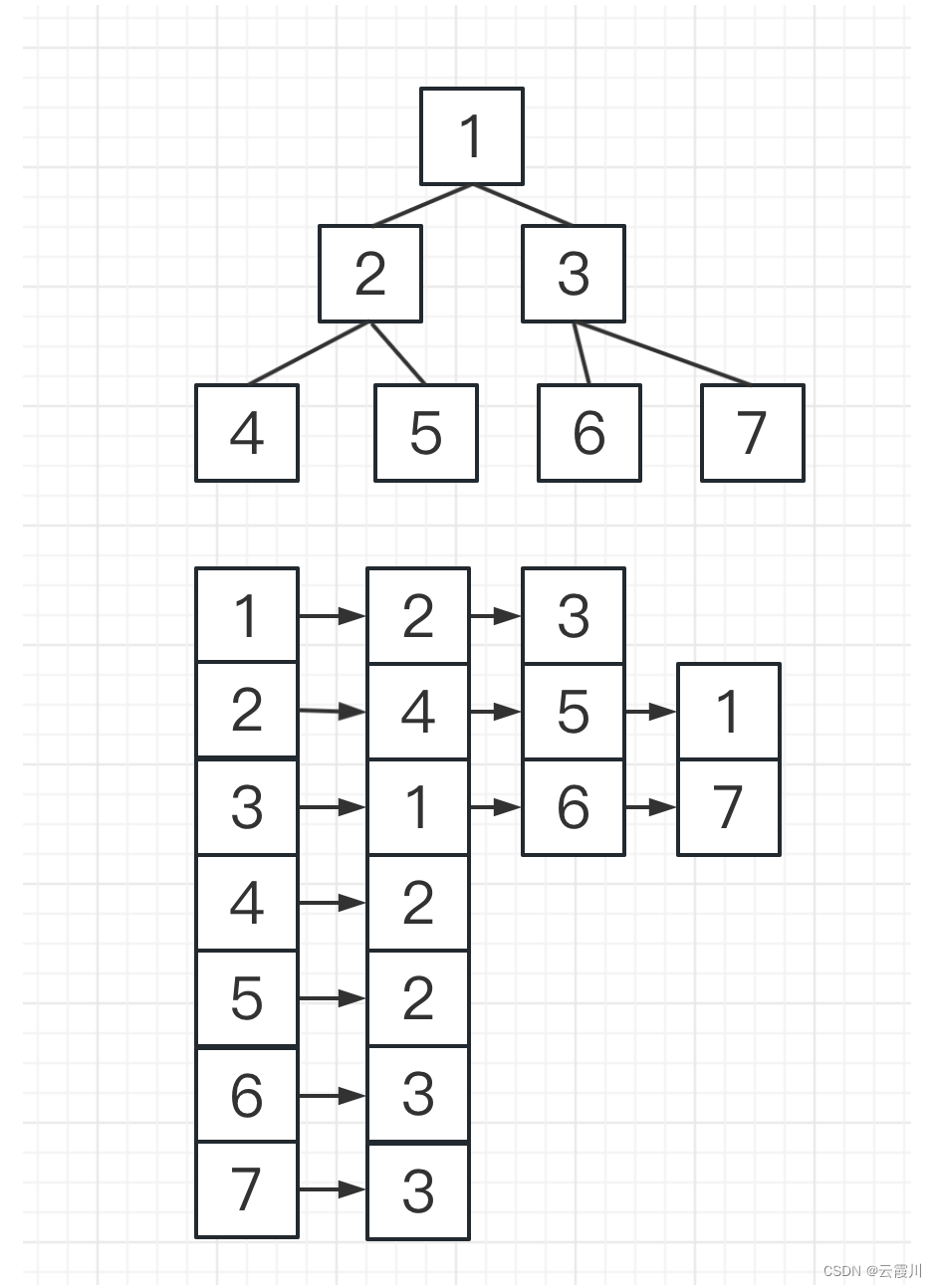
1.树状数组

设计二分，二叉树，位运算，前缀和等思想

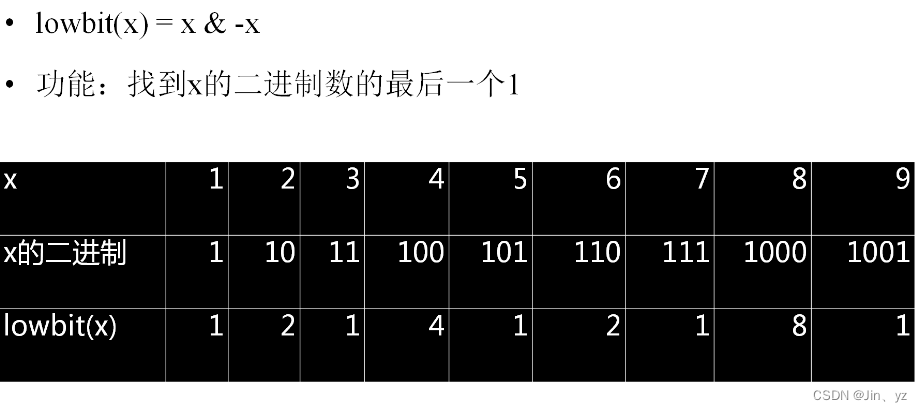
lowbit = x & -x

功能：找到x的二进制数的最后一个1

 

 

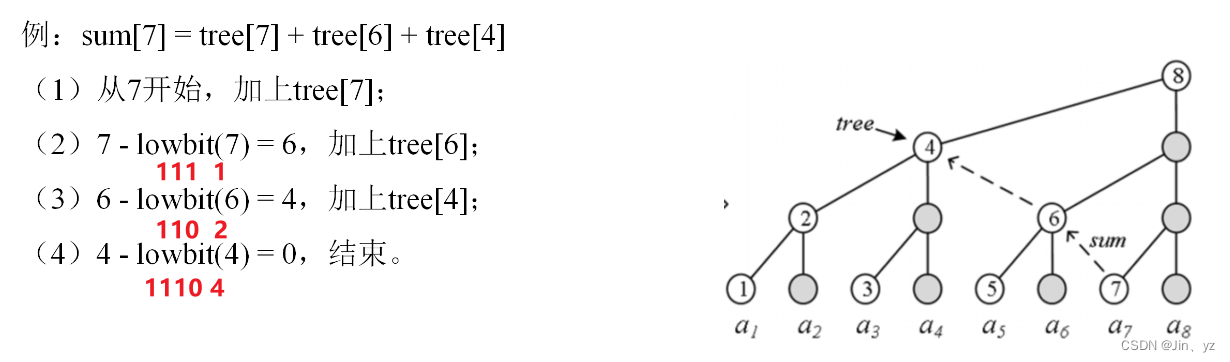
1.1 树状数组模板

def lowbit(x):
    return x &-x
def add (x,d):
    while(x < n) :
        tree[x] +=d
        x+=lowbit(x)
def sum(x):
    ans = 0
    while(x >0):
        ans += tree[x]
        x-=lowbit(x)
        return ans

1.2前缀和应用

1.2.1单点修改，区间查询

def lowbit(x):
    return x &-x
def add (x,d):   # 修改元素a[x],a[x]=a[x]+d
    while(x <= N) :
        tree[x] +=d
        x+=lowbit(x)
def sum(x):   # 前缀和思想,返回前缀和sum=a[1]+a[2]+...a[n]
    ans = 0
    while(x >0):
        ans += tree[x]
        x-=lowbit(x)
        return ans

N=1000
tree =[0]*N
a=[0,4,5,6,7,8,9,10,11,12,13]
for i in range(1,11):   # 计算tree数组，即初始化
    add(i,a[i])
print("old:[5,8]=",sum(8)-sum(4))   # 区间和查询
add(5,100)
print("new:[5,8]",sum(8)-sum(4))

 1.2.2区间修改，区间查询

# python3.6
# -*- coding: utf-8 -*-
# @Time    : 2023/4/29 9:15
# @Author  : Jin
# @File    : 树状数组.py
# @Software: PyCharm

# python3.6
# -*- coding: utf-8 -*-
# @Time    : 2023/4/29 9:15
# @Author  : Jin
# @File    : 树状数组.py
# @Software: PyCharm

def lowbit(x):
    return x &-x
def add1 (x,d):   # 修改元素a[x],a[x]=a[x]+d
    while(x <= N) :
        tree1[x] +=d
        x+=lowbit(x)
def add2(x,d):
    while(x <= N) :
        tree2[x] +=d
        x+=lowbit(x)
def sum1(x):   # 前缀和思想,返回前缀和sum=a[1]+a[2]+...a[n]
    ans = 0
    while(x >0):
        ans += tree1[x]
        x-=lowbit(x)
    return ans
def sum2(x):
    ans = 0
    while (x > 0):
        ans += tree2[x]
        x -= lowbit(x)
    return ans
N=10010
tree1 =[0]*N
tree2 =[0]*N   #2个树状数组
n,m = map(int,input().split())
old=0
a=[0]+[int(i) for i in input().split()]   # 不用a[0]
for i in range(1,n+1):   # 计算tree数组，即初始化
    add1(i,a[i]-old)   # 差分数组原理初始化
    add2(i,(i-1)*(a[i]-old))
    old=a[i]
for _ in range(m):
    g = [int(i) for i in input().split()]
    if (g[0]==1):  # 区间修改
        L,R,d = g[1],g[2],g[3]
        add1(L,d)     # 第一个树状数组，差分
        add1(R+1,-d)
        add2(L,d*(L-1))  # 第二个树状数组，前缀和
        add2(R+1,-d*R)    # d*R = d*(R+1-1)
    else:    # 区间询问
        L,R = g[1],g[2]
        print(R*sum1(R)-sum2(R)-(L-1)*sum1(L-1)+sum2(L-1))

1.2.3 逆序对问题（归并排序）

def merge_sort(L,R):
    if L < R:
        mid = (L+R)//2
        merge_sort(L,mid)
        merge_sort(mid+1,R)
        merge(L,mid,R)
def merge(L,mid,R):
    global res   # 记录答案
    i=L;j=mid+1;t=0
    while(i<=mid and j<=R):  #归并
        a[i]
        a[j]
        if (a[i]>a[j]):     #4 5 / 2 3   L=0 mid=1,R=3
            b[t]=a[j];t+=1;j+=1;
            res = res+(mid-i+1)  # 记录逆序对数量
        else:
            b[t] = a[i];t += 1;i += 1
    # 其中一个处理完了，把剩下的复制过来，直接整体复制
    # 这里注意区间取值，采用的是整体复制的思想，b是辅助数组
    if i<=mid: b[t:R-L+1]=a[i:mid+1]  # 取不到mid+1
    elif j<=R:b[t:R-L+1]=a[j:]
    # 把排序好的b[]复制回去a[]
    a[L:R+1]=b[:R-L+1]
n= int(input())
a = list(map(int,input().split()))
b = [0]*n
res = 0
merge_sort(0,n-1)
print(res)

1.2.4逆序对问题（树状数组）

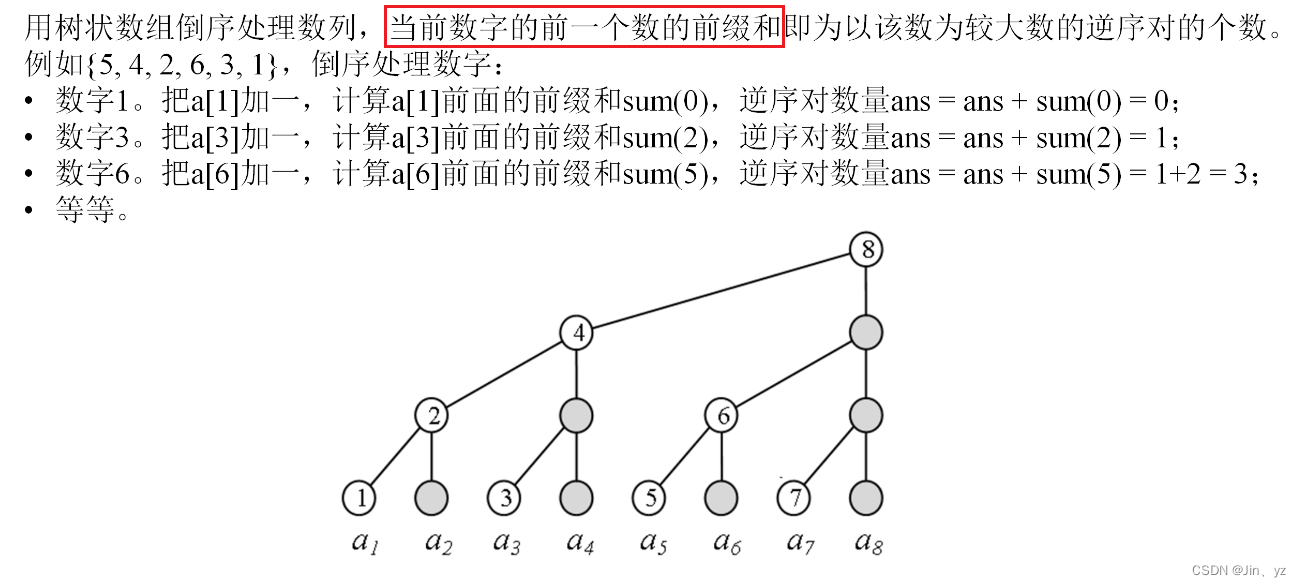
def lowbit(x):
    return x&-x
def update(x,d):    # 更新为 +lowbit(x)
    while(x<=n):
        tree[x]+=d
        x+=lowbit(x)
def sum(x):   # 求和为 -lowbit(x)
    ans=0
    while(x>0):
        ans+=tree[x]
        x-=lowbit(x)
    return ans

n=eval(input())
a = [0]+list(map(int,input().split()))  #从a[1]开始
b=sorted(a)  # 从小到大排序
for i in range(n+1):  # 将a更新为排序后的索引元素+1 [0 1 4 2] -> [1 2 4 3],即转为树状数组下标
    a[a.index(b[i])]=i+1
tree = [0]*(n+1)   # 下标从1开始
res =0
for i in range(len(a)-1,0,-1):   # 倒序处理求逆序对
    update(a[i],1) # 更新a[i]+1
    res+=sum(a[i]-1)
print(res)

1.2.5将元素离散化

def discretization(h):
    b = list(set(h))   # 去重，使得离散化后一样
    b.sort()
    for i in range(len(h)):
        h[i]=b.index(h[i])+1
a=[1,20543,19,376,5460007640,19]
print(a)
discretization(a)
print(a)

2.线段树

2.1线段树介绍

基于二叉树（通过数字模拟二叉树），二分法（mid=（left+right）//2），递归（sys.setrecursionlimit(300000)）

应用背景：

  • 解决区间查询
  • 区间修改问题
  • 多次区间查询最值和区间修改

线段树构建

 

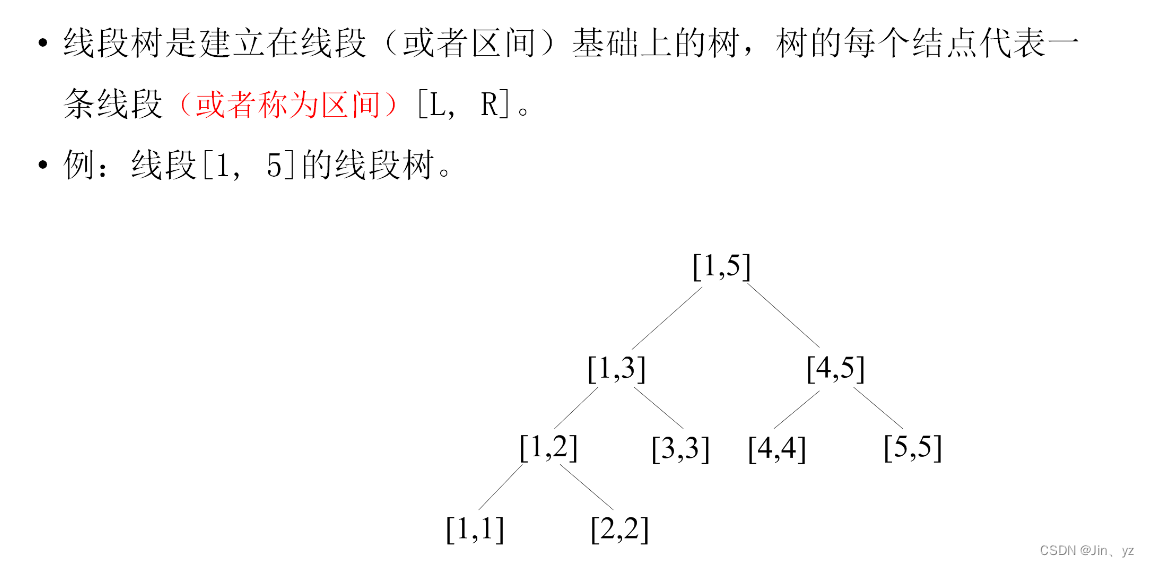
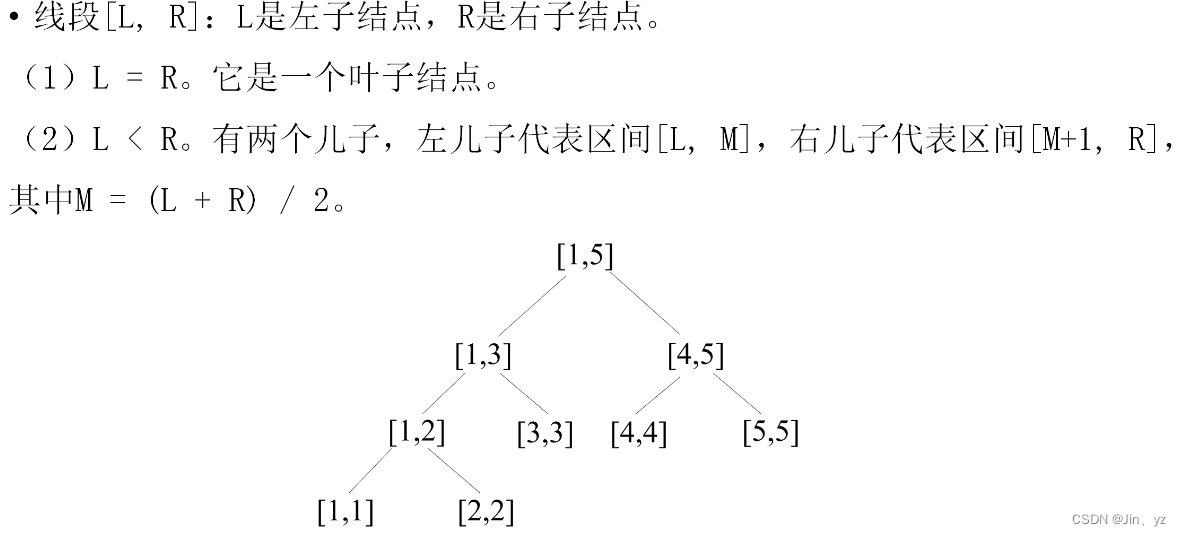
 2.2线段树的树结构

"""
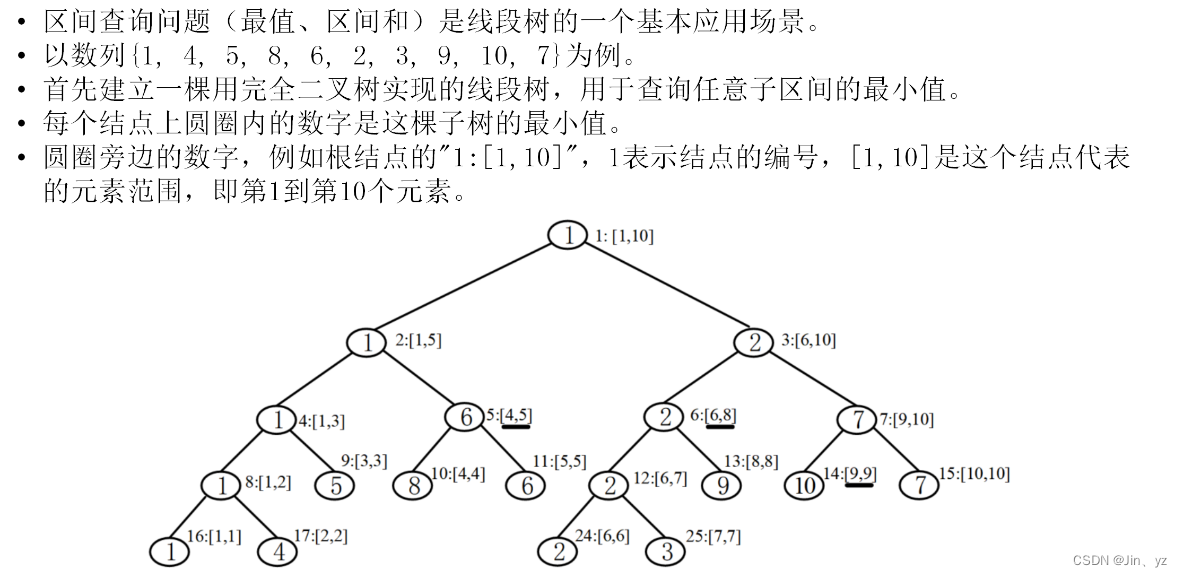
定义根接点为 tree[1]

通过数组模拟存储，空间开为元素个数的四倍，即 4*N
tree[p]
tree[2p]    #左儿子
tree[2p+1]  #右儿子

"""

2.3 利用线段树求最大数例题模板，即单点修改和查询操作模板

"""
def build(p,pl,pr):  #建树
    if pl=pr:
        tree[p]=
        return
    mid=(pl+pr)//2
    build(2*p,pl,mid)
    build(2*p+1,mid+1,pr)
    tree[p]=max( tree[2*p],tree[2*p+1])   # 这步关键

def update(p,pl,pr,L,R,d):
    if L<=pl and pr <=R:  # 说明当前区间完全包含在要查询的区间中
        tree[p]=d
        return
    # 没有完全包含
    mid = (pl+pr)//2
    if L<=mid:    #查左边
        update(2*p,pl,mid,L,R,d)
    if R>mid:     #查右边
        update(2*p+1,mid+1,pr,L,R,d)
    tree[p]=max(tree[2*p],tree[2*p+1])
    return

def query(p,pl,pr,L,R):  # 查 [L R] 区间最值
    res =-inf
    if L<=pl and pr <=R:  # 说明当前区间完全包含在要查询的区间中
        return tree[p]
    # 没有完全包含
    mid = (pl+pr)//2
    if L<=mid:    #查左边 
        return max(res , query(2*p,pl,mid,L,R))
    if R>mid:     #查右边
         return max(res , query(2*p+1,mid+1,pr,L,R))
    tree[p]=max(tree[2*p],tree[2*p+1])
    return
"""

 注意递归问题

L≤mid   ：递归[ pl , mid ]

R>mid  ：递归[ mid+1 , pr ]

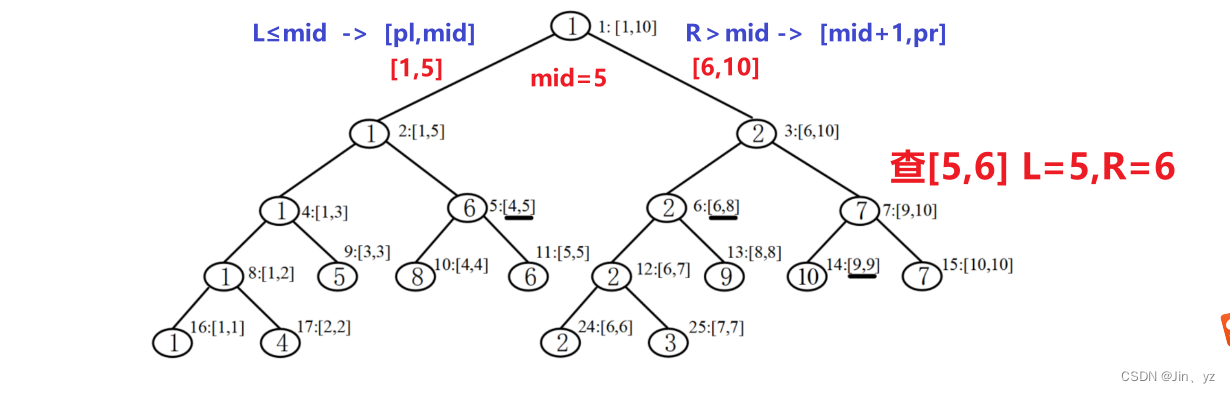
import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)


N=100001
inf=2**50
tree = [0]*4*N  # 初始化树的大小
def build(p,pl,pr):
    if (pl==pr):
        tree[p]=-inf
        return
    mid=(pl+pr)//2
    build(2*p,pl,mid)    #递归构建左孩子 
    build(2*p,mid+1,pr)  #递归构造右孩子
    tree[p]=max(tree[2*p],tree[2*p+1])  #即 push_up操作

def update(p,pl,pr,L,R,d):
    if L<=pl and pr <=R:  # 说明当前区间完全包含在要查询的区间中
        tree[p]=d
        return
    # 没有完全包含
    mid = (pl+pr)//2
    if L<=mid:    #查左边 
        update(2*p,pl,mid,L,R,d)
    if R>mid:     #查右边
        update(2*p+1,mid+1,pr,L,R,d)
    tree[p]=max(tree[2*p],tree[2*p+1])
    return
def query(p,pl,pr,L,R):
    res =-inf
    if L<=pl and pr <=R:  # 说明当前区间完全包含在要查询的区间中
        return tree[p]
    # 没有完全包含
    mid = (pl+pr)//2
    if L<=mid:    #查左边 
        return max(res , query(2*p,pl,mid,L,R))
    if R>mid:     #查右边
         return max(res , query(2*p+1,mid+1,pr,L,R))
    tree[p]=max(tree[2*p],tree[2*p+1])
    return

 

2.4 区间修改的Lazy-tag技术

内部思想

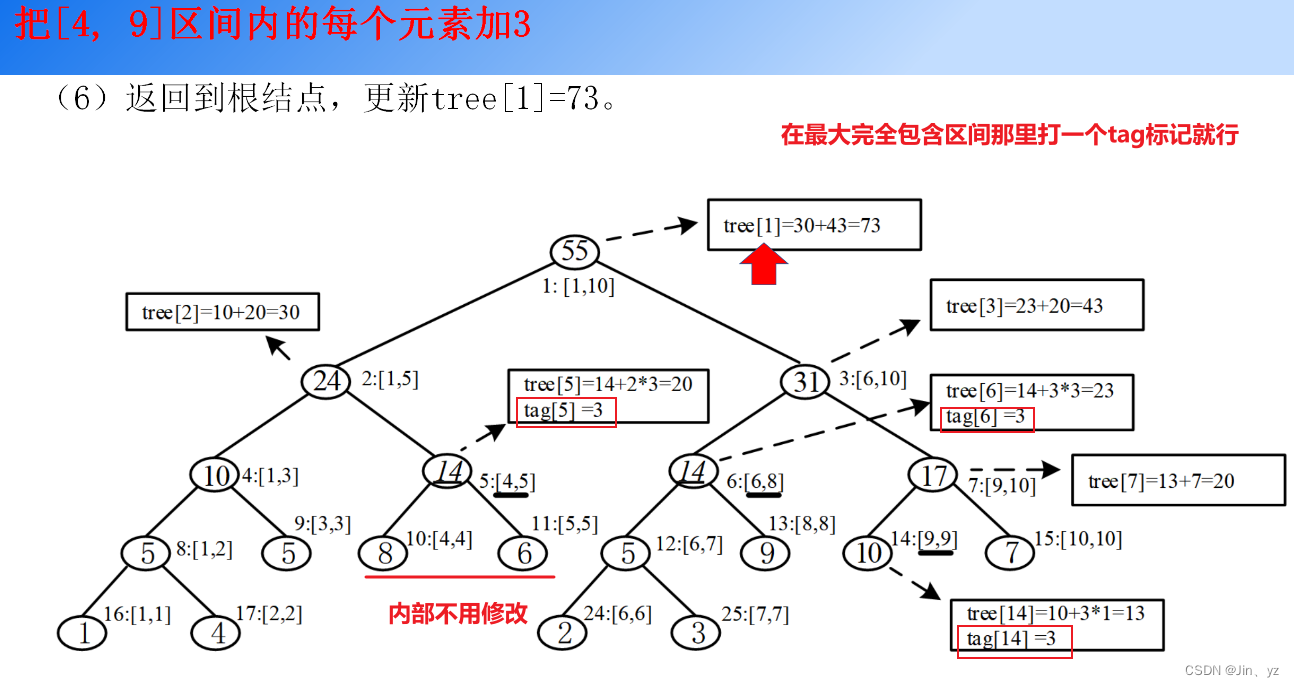
 多次区间修改可能会有冲突，需要push_down（）函数解决

2.4.1区间修改，区间查询例题


import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)


def build(p,pl,pr):
    if (pl==pr):
        tree[p]=a[pl]
        return
    mid=(pl+pr)//2
    build(2*p,pl,mid)    #递归构建左孩子
    build(2*p+1,mid+1,pr)  #递归构造右孩子
    tree[p]=tree[2*p]+tree[2*p+1]  #记录区间和， push_up操作

def update(p,pl,pr,L,R,d):
    if L<=pl and pr <=R:  # 说明当前区间完全包含在要查询的区间中
        addtag(p,pl,pr,d)
        return
    # 没有完全包含
    push_down(p,pl,pr)  # 将懒惰标记传递下去，如果修改区间重叠会有问题
    mid = (pl+pr)//2
    if L<=mid:    #查左边
        update(2*p,pl,mid,L,R,d)
    if R>mid:     #查右边
        update(2*p+1,mid+1,pr,L,R,d)
    tree[p]=tree[2*p]+tree[2*p+1]
    return
def addtag(p,pl,pr,d):   # 给结点p打上标记同时更新tree[p]
    tag[p]+=d
    tree[p]+=d*(pr-pl+1)
def push_down(p,pl,pr):
    if tag[p]>0:  # 有tag标记,需要传递并清空
        mid=(pl+pr)//2
        addtag(2*p,pl,mid,tag[p])   # 传给左孩子
        addtag(2*p+1,mid+1,pr,tag[p])  # 传给右孩子
        tag[p]=0  # 清空当前tag标记

def query(p,pl,pr,L,R):
    if L<=pl and pr <=R:  # 说明当前区间完全包含在要查询的区间中
        return tree[p]
    # 没有完全包含
    push_down(p,pl,pr)  # 如果查询的是标记内部子区间就会有问题！！
    mid = (pl+pr)//2
    res=0
    if L<=mid:    #查左边
        res +=query(2*p,pl,mid,L,R)
    if R>mid:     #查右边
        res +=query(2*p+1,mid+1,pr,L,R)
    return res

n,m = map(int,input().split())
a=[0]+list(map(int,input().split()))
tag=[0]*4*len(a)
tree=[0]*4*len(a)
# 建树
build(1,1,n)
for i in range(m):
    w=list(map(int,input().split()))
    if len(w)==3:  # 区间查询，查询[L,R]区间和
        q,L,R=w
        print(query(1,1,n,L,R))
    else:  # 区间修改，把[L,R]的每个元素加上d
        q,L,R,d=w
        update(1,1,n,L,R,d)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/482370.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

零基础学会 Java，这是你需要按照学习的步骤，加油，新加入的你

零基础学会 Java，这是你需要按照学习的步骤，加油，新加入的你

学习 Java 需要遵循一定的步骤&#xff0c;首先需要学习计算机基础知识&#xff0c;例如算法、数据结构、计算机组成原理等。如果没有相关背景知识&#xff0c;可以参加计算机相关课程进行学习。其次是学习编程基础知识&#xff0c;例如控制流、变量、函数等&#xff0c;你可以…
阅读更多...
详解c++---list模拟实现

详解c++---list模拟实现

目录标题 list的准备工作构造函数push_backlist迭代器beginendinserteraseclearconst迭代器list迭代器区间构造swap现代拷贝构造函数现代赋值重载sizeempty->重载 list的准备工作 首先我们知道list是一个带头双向链表&#xff0c;他的数据就会存储在一个一个的节点里面&…
阅读更多...
Python基础合集 练习22 (错误与异常处理语句2)

Python基础合集 练习22 (错误与异常处理语句2)

‘’’ try: 语句块 except: 语句块2 else ‘’’ class Mobe1(): def init(self) -> None: pass def mob1(self):while True:try:num int(input(请输入一个数: ))result 50 / numprint(result)print(50/{0}{1}.format(num, result))except (ZeroDivisionError, ValueEr…
阅读更多...
时代浪潮已经袭来 AI人工智能频频爆火 ChatGPT改变行业未来

时代浪潮已经袭来 AI人工智能频频爆火 ChatGPT改变行业未来

目录 1 人工智能的发展 1.1人工智能发展历程 1.1.1 人工智能的起源 1.1.2 人工智能发展的起起伏伏 1.1.3 人工智能多元化 2 什么是ChatGPT 2.1 ChatGPT的主要功能 2.2ChatGPT对企业的多种优势 2.3 不必担心ChatGPT带来的焦虑 3 人工智能对行业未来的影响 3.1 人工智…
阅读更多...
UG NX二次开发（C++）-建模-根据UFun创建的Tag_t转换为Body

UG NX二次开发（C++）-建模-根据UFun创建的Tag_t转换为Body

文章目录 1、前言2、用UF_MODL_create_block1创建一个块3、将Tag_t转换为Body出现错误3、解决方法4、结论 1、前言 经常采用UG NX二次开发&#xff08;NXOpen C#&#xff09;&#xff08;UG NX二次开发&#xff08;C#&#xff09;专栏&#xff09;&#xff0c;在用UFun创建一个…
阅读更多...
【Git 入门教程】第十节、Git的常见问题

【Git 入门教程】第十节、Git的常见问题

Git是一个强大的版本控制系统&#xff0c;它可以帮助开发者管理和协调代码库。然而&#xff0c;初学者使用Git时可能会遇到一些问题。本文将列举一些常见的问题&#xff0c;并提供相应的解决方案。 1. Git无法识别文件权限 在使用Git时&#xff0c;有时候你可能会遇到类似于“…
阅读更多...
异构无线传感器网络路由算法研究（Matlab代码实现）

异构无线传感器网络路由算法研究（Matlab代码实现）

目录 &#x1f4a5;1 概述 &#x1f4da;2 运行结果 &#x1f389;3 参考文献 &#x1f468;‍&#x1f4bb;4 Matlab代码 &#x1f4a5;1 概述 ​无线传感器网络(Wireless Sensor Networks, WSN)是一种新型的融合传感器、计算机、通信等多学科的信息获取和处理技术的网络,…
阅读更多...
Ubuntu下跑通 nnUNet v2

Ubuntu下跑通 nnUNet v2

网上关于nnUNet运行的教程大部分是针对nnUNet v1的。但由于nnUNet v2已经推出&#xff0c;而且相对于v1有了很大的更新。所以个人只能啃nnUNet的英文文档参考在Windows上实现nnU-Net v2的环境配置_netv2_无聊的程序猿的博客-CSDN博客 实现了代码的复现。 1.System requirement…
阅读更多...
树与图的存储-邻接表与邻接矩阵-深度广度遍历

树与图的存储-邻接表与邻接矩阵-深度广度遍历

全部代码 全部代码在github acwing 上 正在更新 https://github.com/stolendance/acwing 图论 欢迎star与fork 树与图的存储 无论是树 还是无向图 都可以看成有向图 有向图可以采用邻接矩阵与邻接表进行存储 邻接矩阵 邻接矩阵 采用矩阵存储,graph[i][j] 代表i到j边的权重…
阅读更多...
Python学习15：恺撒密码 B（python123）

Python学习15：恺撒密码 B（python123）

描述 恺撒密码是古罗马凯撒大帝用来对军事情报进行加解密的算法&#xff0c;它采用了替换方法对信息中的每一个英文字符循环替换为字母表序列中该字符后面的第三个字符&#xff0c;即&#xff0c;字母表的对应关系如下&#xff1a;‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪…
阅读更多...
Markdown编辑器快捷方式

Markdown编辑器快捷方式

这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题&#xff0c;有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…
阅读更多...
Linux安装离线版MySql客户端

Linux安装离线版MySql客户端

本文采用rpm安装方式。 下载文件&#xff1a; mysql-community-libs-5.7.41-1.el7.x86_64 mysql-community-common-5.7.41-1.el7.x86_64 mysql-community-client-5.7.41-1.el7.x86_64 本文件可以在MYSQL官网进行下载 MySQL :: Download MySQL Community Server (Archive…
阅读更多...
C语言入门篇——文件操作篇

C语言入门篇——文件操作篇

目录 1、为什么使用文件 2、什么是文件 2.1程序文件 2.2数据文件 2.3文件名 3、文件的打开和关闭 3.1文件指针 3.2文件的打开和关闭 4、文件的顺序读写 5、文件的随机读写 5.1fseek 5.2ftell 5.3rewind 6、文本文件和二进制文件 7、文件读取结束的判定 8、文件…
阅读更多...
玩转肺癌目标检测数据集Lung-PET-CT-Dx ——④转换成PASCAL VOC格式数据集

玩转肺癌目标检测数据集Lung-PET-CT-Dx ——④转换成PASCAL VOC格式数据集

文章目录 关于PASCAL VOC数据集目录结构 ①创建VOC数据集的几个相关目录XML文件的形式 ②读取dcm文件与xml文件的配对关系③创建VOC格式数据集④创建训练、验证集 本文所用代码见文末Github链接。 关于PASCAL VOC数据集 pascal voc数据集是关于计算机视觉&#xff0c;业内广泛…
阅读更多...
【五一创作】Pytroch nn.Unfold() 与 nn.Fold(）图码详解

【五一创作】Pytroch nn.Unfold() 与 nn.Fold(）图码详解

文章目录 Unfold()与Fold()的用途nn.Unfold()Unfold()与Fold() 变化模式图解 nn.Fold()单通道 滑动窗口无重叠模拟图片数据&#xff08;b,3,9,9&#xff09;&#xff0c;通道数 C 为3&#xff0c;滑动窗口无重叠。单通道 滑动窗口有重叠。 卷积等价于&#xff1a;Unfold Matri…
阅读更多...
Hadoop 2：MapReduce

Hadoop 2：MapReduce

理解MapReduce思想 MapReduce的思想核心是“先分再合&#xff0c;分而治之”。 所谓“分而治之”就是把一个复杂的问题&#xff0c;按照一定的“分解”方法分为等价的规模较小的若干部分&#xff0c;然后逐个解决&#xff0c;分别找出各部分的结果&#xff0c;然后把各部分的结…
阅读更多...
从C语言到C++④(第二章_类和对象_上篇)-＞类-＞封装-＞this指针

从C语言到C++④(第二章_类和对象_上篇)-＞类-＞封装-＞this指针

目录 1. 面向对象 1.1 类的引入 1.2 class 关键字 2. 类的访问限定符及封装 2.1 访问限定符 2.2 封装 2.2.2 封装的本质 3. 类的作用域和实例化 3.1 类定义的两种方式 3.2 类的作用域 3.3 类的实例化 3.3.1 声明和定义的区别 4. 类对象模型 4.1 计算类的存储大小…
阅读更多...
Java开发者在Windows环境安装各类开发工具汇总

Java开发者在Windows环境安装各类开发工具汇总

Java开发者在Windows环境安装各类开发工具汇总 前言Java JDK下载配置 Tomcat下载配置 Maven下载配置配置仓库 Nginx下载启动关闭 MySQL下载配置my.ini初始化MySQL数据文件安装MySQL服务启动MySQL登录MySQL重置登录密码 NodeJs下载安装与验证配置NPM Git下载配置git配置ssh免密登…
阅读更多...
Oracle删除列操作：逻辑删除和物理删除

Oracle删除列操作：逻辑删除和物理删除

概念 逻辑删除&#xff1a;逻辑删除并不是真正的删除&#xff0c;而是将表中列所对应的状态字段&#xff08;status&#xff09;做修改操作&#xff0c;实际上并未删除目标列数据或恢复这些列占用的磁盘空间。比如0是未删除&#xff0c;1是删除。在逻辑上数据是被删除了&#…
阅读更多...
【MATLAB数据处理实用案例详解（22）】——基于BP神经网络的PID参数整定

【MATLAB数据处理实用案例详解（22）】——基于BP神经网络的PID参数整定

目录 一、问题描述二、算法仿真2.1 BP_PID参数整定初始化2.2 优化PID2.3 绘制图像 三、运行结果四、完整程序 一、问题描述 基于BP神经网络的PID控制的系统结构如下图所示&#xff1a; 考虑仿真对象&#xff0c;输入为r(k)1.0&#xff0c;输入层为4&#xff0c;隐藏层为5&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023