1. 简明ESKF

简介

本文主要介绍一种特殊正交群 $\text{SO(3)}$ 上的ESKF(Error State Kalman Filter, 误差卡尔曼滤波器)（有时也叫做流形上的ESKF）推导过程。

ESKF基本过程及优点

在现代的大多数IMU系统中，人们往往使用误差状态卡尔曼滤波器（Error State Kalman Filter, ESKF），而非原始状态的卡尔曼滤波器。大部分基于滤波器的LIO或VIO实现，都使用ESKF作为状态估计方法。

相比于传统KF，ESKF的优点如下：

1. 在旋转的处理上，ESKF的状态变量可以采用最小化的参数表达，也就是使用三维变量来表达旋转的增量。而传统的KF则需要使用四元数（$4$维）或更高维的表达（旋转矩阵，$9$维）,要不就得采用带奇异性的表达方式（欧拉角）。
2. ESKF总是在原点附近，距离奇异点较远，并且也不会由于离工作点太远而导致线性化近似不够的问题。
3. ESKF的状态量为小量，其二阶变量相对来说可以忽略。同时大多数雅可比矩阵在小量情况下变得非常简单，甚至可以用单位阵代替。
4. 误差状态的运动学也相比原状态变量要来的更小，因为我们可以把大量更新部分放到原状态变量中。

在ESKF中，我们通常把原状态变量称为名义状态变量（Norminal State），把ESKF中的状态变量称为误差状态变量（Error State）。

ESKF整体流程如下：

• 当IMU测量数据到达时，首先将其积分后，放入名义状态变量中。
• 由于这种做法没有考虑噪声，其结果自然会快速漂移。于是我们希望把误差部分作为误差变量，放入ESKF中。
• ESKF内部会考虑各种噪声和零偏的影响，并且给出误差状态的一个 高斯分布 描述。同时ESKF本身作为一种卡尔曼滤波器，也具有预测过程和修正过程。其中 修正过程 需要依赖 IMU 以外的传感器观测。在修正后，ESKF可以给出 后验的误差高斯分布。
• 随后，我们将这部分误差放入名义状态变量中，并把ESKF置零，这样就完成了一次循环。

---

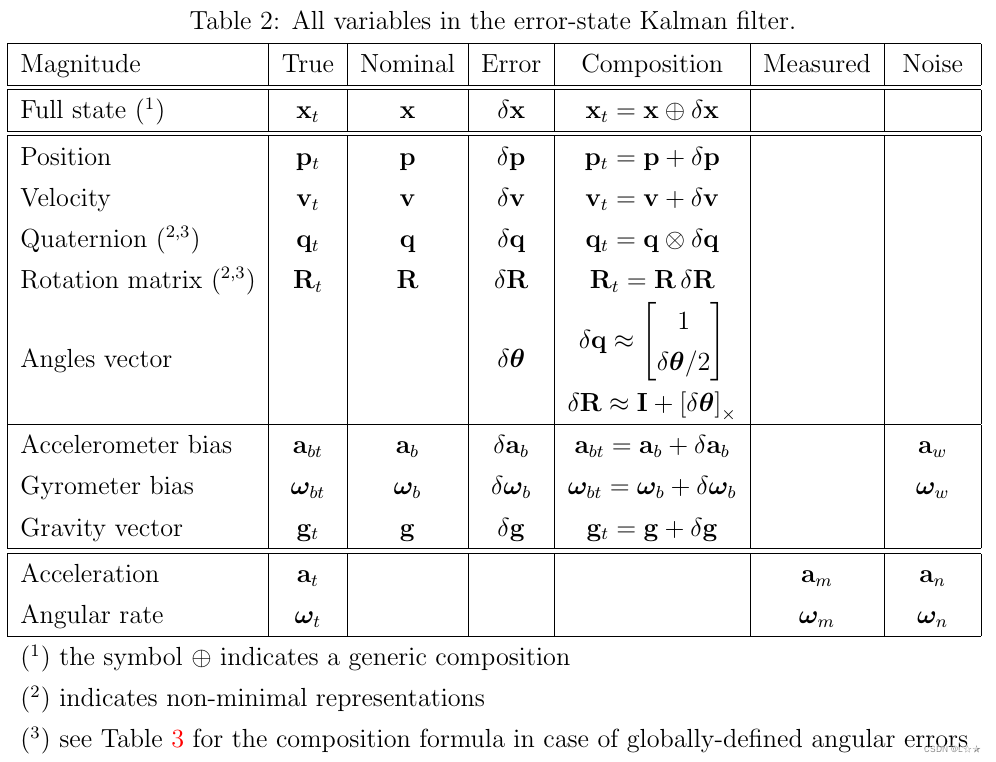
ESKF参数含义

连续时间上的 ESKF状态方程

我们设ESKF的真值状态为：
$$x_t=[p_t,v_t,R_t,b_{at},b_{gt},g_t{]}^{\text{T}}$$
这个状态随时间改变，可以记为$x(t{)}_t$。

在连续时间上，我们记IMU读数为 $\tilde{\omega },\tilde{a}$，那么可以写出状态变量导数 相对于 观测量之间的关系式：
$$\dot{p_t}=v_t\text{\hspace{1em}(1 a)}$$

$${\dot{v}}_t=R_t(\tilde{a}-b_{at}-{\eta }_a)+g\text{\hspace{1em}(1 b)}$$

$${\dot{R}}_t=R_t(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }\text{\hspace{1em}(1 c)}$$

$${\dot{b}}_{gt}={\eta }_{bg}\text{\hspace{1em}(1 d)}$$

$${\dot{b}}_{at}={\eta }_{ba}\text{\hspace{1em}(1 e)}$$

$$\dot{g}=0\text{\hspace{1em}(1 f)}$$

其中，带下标 $t$ 的表示真值。

这里把重力 $g$ 考虑进来的主要理由是方便确定IMU的初始姿态。

• 如果我们不在状态方程里写出重力变量，那么就必须事先确定初始时刻的IMU朝向 $R(0)$，才能执行后续的计算。此时IMU的姿态就是相对于初始的水平面来描述的。

• 而如果把重力写出来，就可以设IMU的初始姿态为单位矩阵$R=I$，而把重力方向作为IMU当前姿态相对于水平面的一个度量。

两种方法都是可行的，不过将重力方向单独表达出来会使初始状态表达更为简单，同时还可以增加一些线性性。

如果把观测量 和 噪声量 整理成一个向量，我们也可以把上式整理成矩阵形式。不过这里的矩阵形式将含有很多的 零项，相比于上式不会有明显的简化，所以这里采用散开的公式表示。

误差状态方程推导

下面我们推导误差状态方程。首先定义误差状态变量为：
$$p_t=p+\delta p\text{\hspace{1em}(2 a)}$$

$$v_t=v+\delta v\text{\hspace{1em}(2 b)}$$

$$R_t=R\delta R或q_t=q\delta q\text{\hspace{1em}(2 c)}$$

$$b_{gt}=b_g+\delta b_g\text{\hspace{1em}(2 d)}$$

$$b_{at}=b_a+\delta b_a\text{\hspace{1em}(2 e)}$$

$$g_t=g+\delta g\text{\hspace{1em}(2 f)}$$

其中，不带下标的就是名义状态变量。名义状态变量 的运动学方程 与真值相同，只是 不需要考虑噪声（因为噪声在误差状态方程中考虑了） 。 其中旋转部分的$\delta R$ 可以用它的李代数 $\text{Exp}(\delta \theta )$来表示，此时旋转公式也需要改成用指数形式来表达。

关于误差变量的平移、零偏和重力公式，都很容易的而出对应的时间导数表达式，只需要在等式两侧分别对时间求导即可：
$$\delta \dot{p}=\delta v\text{\hspace{1em}(3 a)}$$

$$\delta \dot{b_g}={\eta }_g\text{\hspace{1em}(3 b)}$$

$$\delta \dot{b_a}={\eta }_a\text{\hspace{1em}(3 c)}$$

$$\delta g=0\text{\hspace{1em}(3 d)}$$

而速度、旋转两式由于和$\delta R$有关系，所以需要单独推导。

误差状态的旋转项

对旋转式两侧求时间导数，可得：
$$\begin{array}{rl}{\dot{R}}_t& =\dot{R}\text{Exp}(\delta \theta )+R\dot{\text{Exp}(\delta \theta )}\\ & =R_t(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }\end{array}\text{\hspace{1em}(4)}$$
该式右侧的$\dot{\text{Exp}(\delta \theta )}$ 满足：
$$\dot{\text{Exp}(\delta \theta )}=\text{Exp}(\delta \theta )\delta {\dot{\theta }}^{\wedge }\text{\hspace{1em}(5)}$$
因此，公式（4）中第一个式子可以写成：
$$\dot{R}\text{Exp}(\delta \theta )+R\dot{\text{Exp}(\delta \theta )}=R(\tilde{\omega }-b_g{)}^{\wedge }\text{Exp}(\delta \theta )+R\text{Exp}(\delta \theta )\delta {\dot{\theta }}^{\wedge }\text{\hspace{1em}(6)}$$

而 第二个式子可以写成：

$$R_t(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }=R\text{Exp}(\delta \theta )(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }\text{\hspace{1em}(7)}$$

比较公式（6）、（7），将$\delta \dot{\theta }$ 移到一侧，约掉两侧左边的$R$ ，整理类似项，不难得到：

$$\text{Exp}(\delta \theta )\delta {\dot{\theta }}^{\wedge }=\text{Exp}(\delta \theta )(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }-(\tilde{\omega }-b_g{)}^{\wedge }\text{Exp}(\delta \theta )\text{\hspace{1em}(8)}$$
注意到 $\text{Exp}(\delta \theta )$ 本身是一个 $\text{SO(3)}$ 矩阵，我们利用$\text{SO(3)}$ 上的伴随性质：
$${\varphi }^{\wedge }R=R(R^{\text{T}}\varphi {)}^{\wedge }\text{\hspace{1em}(9)}$$

来交换公式（8）中的 $\text{Exp}(\delta \theta )$ ：
$$\begin{array}{rl}\text{Exp}(\delta \theta )\delta {\dot{\theta }}^{\wedge }& =\text{Exp}(\delta \theta )(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }-\text{Exp}(\delta \theta )\text{Exp}(-\delta \theta )(\tilde{\omega }-b_g{)}^{\wedge }\\ & =\text{Exp}(\delta \theta )\left[(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }-\text{Exp}(-\delta \theta )(\tilde{\omega }-b_g{)}^{\wedge }\right]\\ & \approx \text{Exp}(\delta \theta )\left[(\tilde{\omega }-b_{gt}-{\eta }_g{)}^{\wedge }-{\left((I-\delta {\theta }^{\wedge })(\tilde{\omega }-b_g)\right)}^{\wedge }\right]\\ & =\text{Exp}(\delta \theta ){\left[b_g-b_{gt}-{\eta }_g+\delta {\theta }^{\wedge }\tilde{\omega }-\delta {\theta }^{\wedge }{b}_g\right]}^{\wedge }\\ & =\text{Exp}(\delta \theta ){\left[(-\tilde{\omega }+b_g{)}^{\wedge }\delta \theta -\delta b_g-{\eta }_g\right]}^{\wedge }\end{array}\text{\hspace{1em}(10)}$$

约掉公式（10）等式左侧的系数，可得：

$$\delta \dot{\theta }\approx -(\tilde{\omega }-b_g{)}^{\wedge }\delta \theta -\delta b_g-{\eta }_g\text{\hspace{1em}(11)}$$

误差状态的速度项

接下来考虑速度方程的误差形式。同样地，对两侧求时间导数，就可以得到$\delta \dot{v}$ 的表达式。等式左侧为：
$$\begin{array}{rl}{\dot{v}}_t& =R_t(\tilde{a}-b_{at}-{\eta }_a)+g_t\\ & =R\text{Exp}(\delta \theta )(\tilde{a}-b_a-\delta b_a-{\eta }_a)+g+\delta g\\ & \approx R(I+\delta {\theta }^{\wedge })(\tilde{a}-b_a-\delta b_a-{\eta }_a)+g+\delta g\\ & \approx R\tilde{a}-R{b}_a-R\delta b_a-R{\eta }_a+R\delta {\theta }^{\wedge }a-R\delta {\theta }^{\wedge }{b}_a+g+\delta g\\ & =R\tilde{a}-R{b}_a-R\delta b_a-R{\eta }_a-R{\tilde{a}}^{\wedge }\delta \theta +R{b}_a^{\wedge }\delta \theta +g+\delta g\end{array}\text{\hspace{1em}(12)}$$
在公式（12）中，由第三行向第四行推导时，需要忽略 $\delta {\theta }^{\wedge }$ 与 $\delta b_a$，${\eta }_a$ 相乘的二阶小量。

从第四行推第五行则用到了叉乘符号交换顺序后，需要加负号的性质。

另一方面，等式右侧为：
$$\dot{v}+\theta \dot{v}=R(\tilde{a}-b_a)+g+\delta \dot{v}\text{\hspace{1em}(13)}$$
因为上面两式相等，可以得到：
$$\delta \dot{v}=-R(\tilde{a}-b_a{)}^{\wedge }\delta \theta -R\delta b_a-R{\eta }_a+\delta g\text{\hspace{1em}(14)}$$
这样我们就得到了$\delta v$的运动学模型。

需要补充一句，由于上式中${\eta }_a$ 是一个零均值白噪声，它乘上任意旋转矩阵之后，仍然是一个零均值白噪声，而且由于$R^{\text{T}}R=I$，其协方差矩阵也不变。

所以，公式（14）可以简化为：
$$\delta \dot{v}=-R(\tilde{a}-b_a{)}^{\wedge }\delta \theta -R\delta b_a-{\eta }_a+\delta g\text{\hspace{1em}(15)}$$

完整误差变量的运动学方程

至此，我们可以把误差变量的运动学方程整理如下：
$$\delta \dot{p}=\delta v\text{\hspace{1em}(16 a)}$$

$$\delta \dot{v}=-R(\tilde{a}-b_a{)}^{\wedge }\delta \theta -R\delta b_a-{\eta }_a+\delta g\text{\hspace{1em}(16 b)}$$

$$\delta \dot{\theta }\approx -(\tilde{\omega }-b_g{)}^{\wedge }\delta \theta -\delta b_g-{\eta }_g\text{\hspace{1em}(16 c)}$$

$$\delta \dot{b_g}={\eta }_g\text{\hspace{1em}(16 d)}$$

$$\delta \dot{b_a}={\eta }_a\text{\hspace{1em}(16 e)}$$

$$\delta g=0\text{\hspace{1em}(16 f)}$$

---

离散时间上的ESKF运动学方程

从连续时间状态方程，推出离散时间的状态方程并不困难，不妨直接来列写它们。

名义状态变量的离散时间运动学方程可以写为：
$$p(t+\Delta t)=p(t)+v\Delta t+\frac{1}{2}(R(\tilde{a}-b_a))\Delta t^2+\frac{1}{2}g\Delta t^2\text{\hspace{1em}(17 a)}$$

$$v(t+\Delta t)=v(t)+R(\tilde{a}-b_a))\Delta t+g\Delta t\text{\hspace{1em}(17 b)}$$

$$R(t+\Delta t)=R(t)\text{Exp}((\tilde{\omega }-b_g)\Delta t)\text{\hspace{1em}(17 c)}$$

$$b_g(t+\Delta t)=b_g(t)\text{\hspace{1em}(17 d)}$$

$$b_a(t+\Delta t)=b_a(t)\text{\hspace{1em}(17 e)}$$

$$g(t+\Delta t)=g(t)\text{\hspace{1em}(17 f)}$$

公式（17） 只需要在上面基础上，添加零偏项和重力项即可。

而误差状态的离散形式，只需要处理连续形态中的旋转部分。参考角速度的积分公式，可以将误差状态方程写为：
$$\delta p(t+\Delta t)=\delta p+\delta v\Delta t\text{\hspace{1em}(18 a)}$$

$$\delta v(t+\Delta t)=\delta v+(-R(\tilde{a}-b_a{)}^{\wedge }\delta \theta -R\delta b_a+\delta g)\Delta t+{\eta }_v\text{\hspace{1em}(18 b)}$$

$$\delta \theta (t+\Delta t)=\text{Exp}(-(\widetilde{\omega -b_a})\Delta t)\delta \theta -\delta b_g\Delta t-{\eta }_{\theta }\text{\hspace{1em}(18 c)}$$

$$\delta b_g(t+\Delta t)=\delta b_g+{\eta }_g\text{\hspace{1em}(18 d)}$$

$$\delta b_a(t+\Delta t)=\delta b_a+{\eta }_a\text{\hspace{1em}(18 e)}$$

$$\delta g(t+\Delta t)=\delta g\text{\hspace{1em}(18 f)}$$

公式（18）中，需要注意的是：

• 右侧部分省略了括号里的$(t)$ 以简化公式；
• 关于旋转部分的积分，我们可以将连续形式 看成关于 $\delta \theta$ 的微分方程，然后求解。求解过程类似于对角速度进行积分；
• 噪声项不参与递推，需要把它们单独归入噪声部分中。连续时间的噪声项可以视为随机过程中的能量谱密度，而离散时间下的噪声变量就是我们日常看到的随机变量了。这些噪声随机变量的标准差可以列写如下：

$$\sigma ({\eta }_v)=\Delta t{\sigma }_a,\sigma ({\eta }_{\theta })=\Delta t{\sigma }_g,\sigma ({\eta }_g)=\sqrt{\Delta t}{\eta }_{bg},\sigma ({\eta }_a)=\sqrt{\Delta t}{\sigma }_{ba}\text{\hspace{1em}(19)}$$

其中，前两式中的$\Delta t$是由积分关系导致的。

至此，我们给出了如何在ESKF中进行IMU递推的过程，对应于卡尔曼滤波器中的状态方程。

为了让滤波器收敛，我们通常需要外部的观测来对卡尔曼滤波器进行修正，也就是所谓的组合导航。当然，组合导航的方法有很多，从传统的EKF，到本节介绍的ESKF，以及预积分和图优化技术，都可以应用于组合导航中。

---

ESKF的运动过程

根据上述讨论，我们可以写出ESKF的运动过程。

误差状态变量$\delta x$ 的离散时间运动方程已经在上式给出，我们可以整体地记为：
$$\delta x=f(\delta x)+w,w\sim \mathcal{N}(0,Q)\text{\hspace{1em}(20)}$$
其中，

$w$为噪声，

按照之前定义，$Q$应该为：
$$Q=\text{diag}\left(0_3,\text{Cov}({\eta }_v),\text{Cov}({\eta }_{\theta }),\text{Cov}({\eta }_g),\text{Cov}({\eta }_a),0_3\right)\text{\hspace{1em}(21)}$$
两侧的零是由于第一个和最后一个方程，本身没有噪声导致的。

为了保持与EKF的符号通一，我们计算运动方程的线性化形式：
$$\delta x=\mathbf{F}\delta x+w\text{\hspace{1em}(22)}$$
其中，$\mathbf{F}$为线性化后的雅可比矩阵。

由于我们列写的运动方程以及是线性化的了，只需要把他么的线性系统拿出来即可：
$$\mathbf{F}=\left[\begin{array}{cccccc}I& I\Delta t& 0& 0& 0& 0\\ 0& I& -R(\tilde{a}-b_a{)}^{\wedge }\Delta t& -R\Delta t& 0& I\Delta t\\ 0& 0& \text{Exp}(-(\tilde{\omega }-b_g)\Delta t)& 0& -I\Delta t& 0\\ 0& 0& 0& I& 0& 0\\ 0& 0& 0& 0& I& 0\\ 0& 0& 0& 0& 0& I\end{array}\right]\text{\hspace{1em}(23)}$$
在此基础上，我们执行ESKF的预测过程。预测过程包括对名义状态的预测（IMU积分），以及对误差状态的预测：
$$\delta x_{\text{pred}}=\mathbf{F}\delta x\text{\hspace{1em}(24 a)}$$

$${\mathbf{P}}_{\text{pred}}={\mathbf{F}\mathbf{P}\mathbf{F}}^{\text{T}}+\mathbf{Q}\text{\hspace{1em}(24 b)}$$

不过，由于ESKF的误差状态，在每次更新以后都会被重置，因此运动方程的均值部分没有太大意义，而方差部分则可以指导整个误差估计的分布情况。

---

ESKF的更新过程

前面介绍的是ESKF的运动过程，现在我们来考虑更新过程。

假设一个抽象的传感器能够对状态变量产生观测，其观测方式为抽象的$h$ ，那么可以写为：
$$z=h(x)+v,v\sim \mathcal{N}(0,\mathbf{V})\text{\hspace{1em}(25)}$$
其中，

$z$是观测数据 ，

$v$ 是观测噪声，

$\mathbf{V}$ 为该噪声的协方差矩阵。由于变量里已经有$R$了，这里我们换个符号。

在传统的EKF中，我们可以直接对观测方程线性化，求出预测方程相对于状态变量的雅可比矩阵 ，进而更新卡尔曼滤波器。

而在ESKF中，我们当前拥有名义状态 $x$ 以及误差状态 $\delta x$ 的估计，且希望更新的是误差状态，因此要计算观测方程，相比于误差状态的雅可比矩阵：
$$\mathbf{H}=\frac{\partial h}{\partial \delta x}\text{\hspace{1em}(26)}$$
然后再计算卡尔曼增益，进而计算误差状态的更新过程：
$$\mathbf{K}={\mathbf{P}}_{\text{pred}}{\mathbf{H}}^{\text{T}}(\mathbf{H}{\mathbf{P}}_{\text{pred}}{\mathbf{H}}^{\text{T}}+\mathbf{V}{)}^{-1}\text{\hspace{1em}(27 a)}$$

$$\delta x=\mathbf{K}(z-h(x_t))\text{\hspace{1em}(27 b)}$$

$$\mathbf{P}=(\mathbf{I}-\mathbf{K}\mathbf{H}){\mathbf{P}}_{\text{pred}}\text{\hspace{1em}(27 c)}$$

其中，

$\mathbf{K}$ 为卡尔曼增益，

${\mathbf{P}}_{\text{pred}}$ 为预测的协方差矩阵，

最后的 $\mathbf{P}$ 为修正后的 协方差矩阵。

这里$\mathbf{H}$ 的计算可以通过链式法则来生成：
$$\mathbf{H}=\frac{\partial h}{\partial x}\frac{\partial x}{\partial \delta x}\text{\hspace{1em}(28)}$$
其中，

第一项，只需要对观测方程进行线性化，

第二项，根据我们之前对状态变量的定义，可以得到：
$$\frac{\partial x}{\partial \delta x}=\text{diag}\left({\mathbf{I}}_3,{\mathbf{I}}_3,\frac{\partial \text{Log}(R(\text{Exp}(\delta \theta )))}{\partial \delta \theta },{\mathbf{I}}_3,{\mathbf{I}}_3,{\mathbf{I}}_3\right)\text{\hspace{1em}(29)}$$
其他几种都是平凡的，只有旋转部分，因为$\delta \theta$ 定义为 $R$得到右称，我们用右称的BCH即可：
$$\frac{\partial \text{Log}(R(\text{Exp}(\delta \theta )))}{\partial \delta \theta }={\mathbf{J}}_r^{-1}(\mathbf{R})\text{\hspace{1em}(30)}$$
最后，我们可以给每个变量加下标$k$ ，表示在 $k$ 时刻进行状态估计。

ESKF的误差状态后续处理

在经过预测和更新过程之后，我们修正了误差状态的估计。接下来，只需要把误差状态 归入名义状态，然后重置ESKF即可。

归入部分，可以简单地写为：
$${\mathbf{p}}_{k+1}={\mathbf{p}}_k+\delta {\mathbf{p}}_k\text{\hspace{1em}(30 a)}$$

$${\mathbf{v}}_{k+1}={\mathbf{v}}_k+\delta {\mathbf{v}}_k\text{\hspace{1em}(30 b)}$$

$${\mathbf{R}}_{k+1}={\mathbf{R}}_k\text{Exp}(\delta {\mathbf{\theta }}_k)\text{\hspace{1em}(30 c)}$$

$${\mathbf{b}}_{g,k+1}={\mathbf{b}}_{g,k}+\delta {\mathbf{b}}_{g,k}\text{\hspace{1em}(30 d)}$$

$${\mathbf{b}}_{a,k+1}={\mathbf{b}}_{a,k}+\delta {\mathbf{b}}_{a,k}\text{\hspace{1em}(30 e)}$$

$${\mathbf{g}}_{k+1}={\mathbf{g}}_k+\delta {\mathbf{g}}_k\text{\hspace{1em}(30 f)}$$

有些文献里，也会定义为广义的状态变量加法：
$${\mathbf{x}}_{k+1}={\mathbf{x}}_k\oplus \delta {\mathbf{x}}_k\text{\hspace{1em}(31)}$$
这种写法，可以简化整体的表达式。不过，如果公式里出现太多的广义加减法，可能让人不好马上辨别它们的具体含义，所以本文倾向于将各状态分别写开，或者直接用加法而非广义加法符号。

ESKF的重置分为均值部分 和 协方差部分。

均值部分可以简单地实现为：
$$\delta \mathbf{x}=0\text{\hspace{1em}(32)}$$
由于均值被重置了，之前我们描述的是关于 ${\mathbf{x}}_k$ 的切空间中的协方差，而现在描述的是 ${\mathbf{x}}_{k+1}$ 中的协方差。

这次重置会来带来一些微小的差异，主要影响旋转部分。事实上，在重置前，卡尔曼滤波器刻画了${\mathbf{x}}_{\text{pred}}$ 切空间处的一个高速分布 $\mathcal{N}(\delta \mathbf{x},\mathbf{P})$，而重置之后，应该刻画 ${\mathbf{x}}_{\text{pred}}⊞\delta \mathbf{x}$ 处的一个 $\mathcal{N}(\delta \mathbf{x},{\mathbf{P}}_{\text{reset}})$ 。

我们设 重置前的名义旋转估计为 ${\mathbf{R}}_k$， 误差状态为$\delta \mathbf{\theta }$ , 卡尔曼滤波器的增量计算结果为 $\delta {\mathbf{\theta }}_k$， 注意此处的 $\delta {\mathbf{\theta }}_k$ 是已知的，而 $\delta \mathbf{\theta }$是一个随机变量。

重置之后的名义旋转部分为：
$${\mathbf{R}}^{+}\text{Exp}(\delta {\mathbf{\theta }}^{+})={\mathbf{R}}_k\text{Exp}(\delta {\mathbf{\theta }}_k)\text{Exp}(\delta {\mathbf{\theta }}^{+})={\mathbf{R}}_k\text{Exp}(\delta \mathbf{\theta })\text{\hspace{1em}(33)}$$
不难得到：
$$\text{Exp}(\delta {\mathbf{\theta }}^{+})=\text{Exp}(-\delta {\mathbf{\theta }}_k)\text{Exp}(\delta \mathbf{\theta })\text{\hspace{1em}(34)}$$
注意这里的 $\delta \mathbf{\theta }$ 为小量，利用线性化后的BCH公式，可以得到：
$$\delta {\mathbf{\theta }}^{+}=-\delta {\mathbf{\theta }}_k+\delta \mathbf{\theta }-\frac{1}{2}\delta {\mathbf{\theta }}_k^{\wedge }\delta \mathbf{\theta }+o((\delta \mathbf{\theta }{)}^2)\text{\hspace{1em}(35)}$$
于是有：
$$\frac{\partial \delta {\mathbf{\theta }}^{+}}{\partial \delta \mathbf{\theta }}\approx \mathbf{I}-\frac{1}{2}\delta {\mathbf{\theta }}_k^{\wedge }\text{\hspace{1em}(36)}$$
公式（36）表明，重置前后的误差状态，相差一个旋转方面的小雅克比矩阵，我们记作：
$${\mathbf{J}}_{\mathbf{\theta }}=\mathbf{I}-\frac{1}{2}\delta {\mathbf{\theta }}_k^{\wedge }\text{\hspace{1em}(37)}$$
把这个小雅可比矩阵 放到整个状态变量的维度下，并保持其他部分为单位矩阵，可以得到一个完整的雅可比矩阵：
$${\mathbf{J}}_{\mathbf{k}}=\text{diag}({\mathbf{I}}_3,{\mathbf{I}}_3,{\mathbf{I}}_{\mathbf{\theta }},{\mathbf{I}}_3,{\mathbf{I}}_3,{\mathbf{I}}_3)\text{\hspace{1em}(38)}$$
因此，把误差状态的均值归零的同时，它们的协方差矩阵也应该进行线性变换：
$${\mathbf{P}}_{\text{reset}}={\mathbf{J}}_k\mathbf{P}{\mathbf{J}}_k^{\text{T}}\text{\hspace{1em}(39)}$$
不过，由于$\delta {\mathbf{\theta }}_k$ 并不大，这里的 ${\mathbf{J}}_k$ 仍然十分接近于单位矩阵，所以大部分材料里并不处理这一项，而是直接把前面估计的 $\mathbf{P}$ 矩阵作为下一个时刻的起点。

但是本文仍然要介绍这一点，该问题实际意义是做了 切空间投影，即：把一个切空间中的高斯分布投影到另一个切空间中。

小结

本文主要介绍了$\text{SO}(3)$ 流形上的ESKF，相比于四元数形式或者欧拉角形式，更为简单，无需自定义太多符号。

本文主要参考高博知乎