各位朋友们,大家五一劳动节快乐啊,在这里祝大家假期玩得愉快!但是在玩耍的期间不要忘记了敲代码哦。今天我为大家分享的是二叉树的第四篇,废话不多说,我们一起来看看吧。
文章目录
- 二叉树的最近公共祖先
- 题目要求
- 做题思路
- 方法一
- 代码实现
- 方法二
- 代码实现
- 根据二叉树创建字符串
- 题目要求
- 做题思路
二叉树的最近公共祖先
leetcode之二叉树的最近公共祖先(难度:中等)
题目要求
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
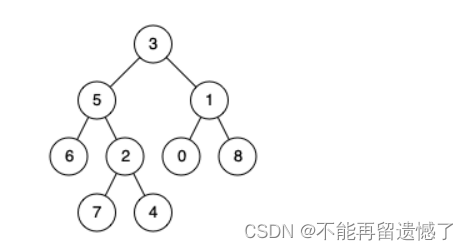
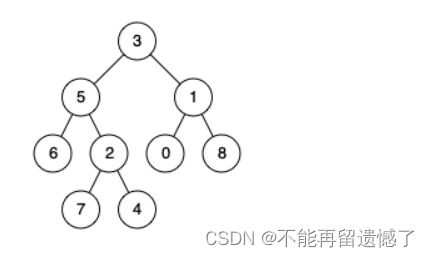
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
}
}
做题思路
做这个题呢,我们有两种方法:
方法一
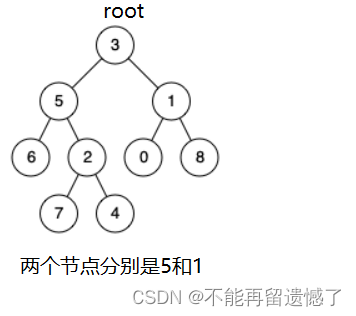
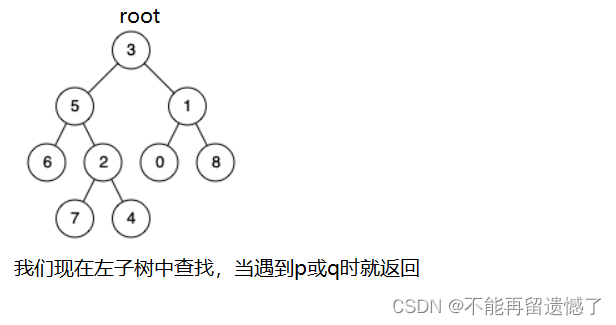
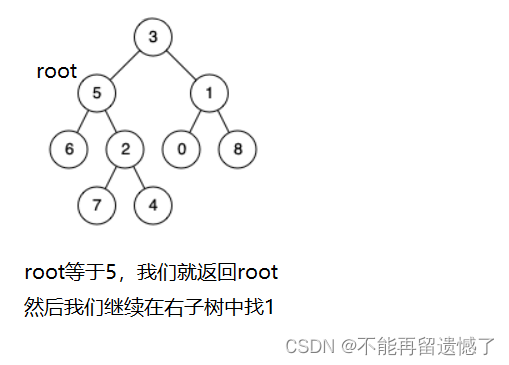
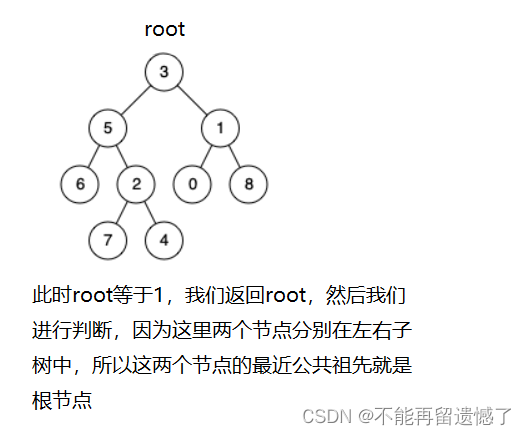
通过root根节点的移动在左子树和右子树中来找这两个节点,如果这两个节点分别在左子树和右子树中,我们就返回根节点,如果这两个节点都在左子树或者右子树,我们就返回那个深度更大的节点,这个节点就是两个节点的最近公共祖先。
代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) {
return null;
}
if(root == p || root == q) {
return root;
}
TreeNode leftRet = lowestCommonAncestor(root.left,p,q);
TreeNode rightRet = lowestCommonAncestor(root.right,p,q);
if(leftRet != null && rightRet != null) {
return root;
}else if(leftRet != null) {
return leftRet;
}else {
return rightRet;
}
}
}
方法二
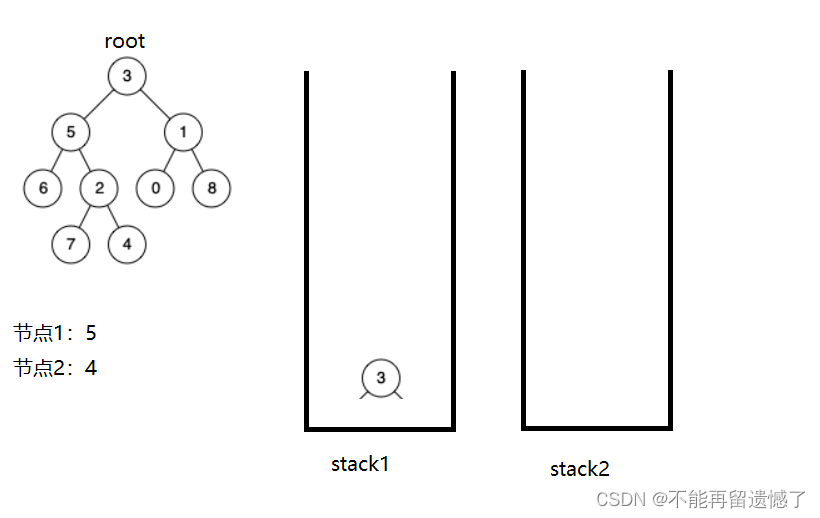
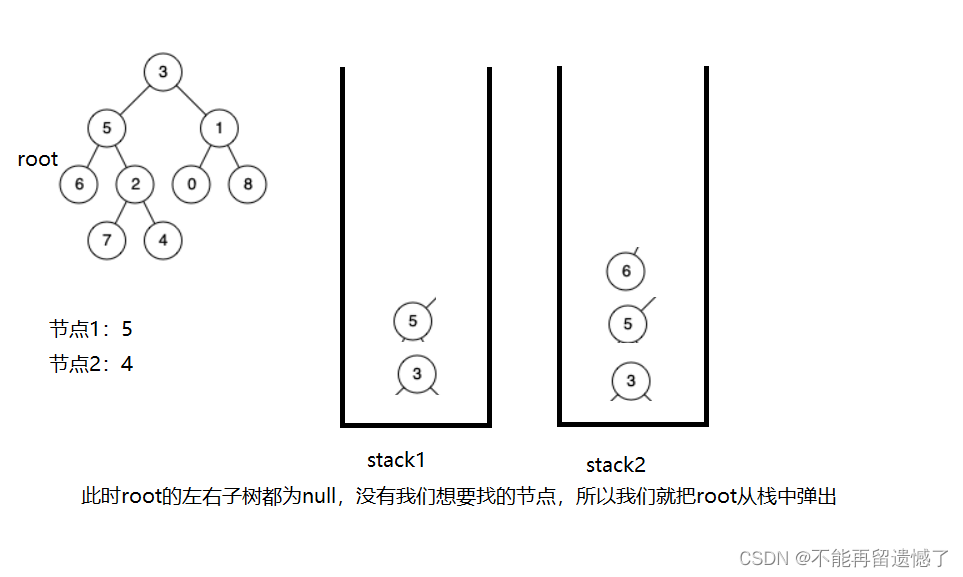
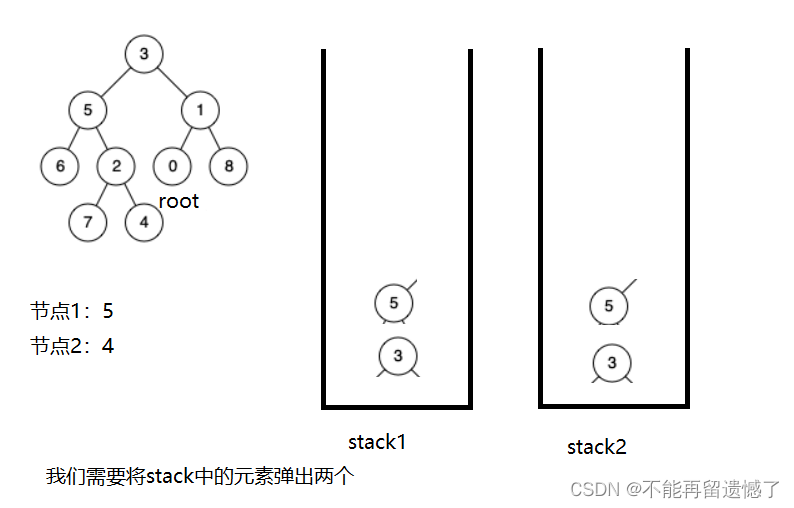
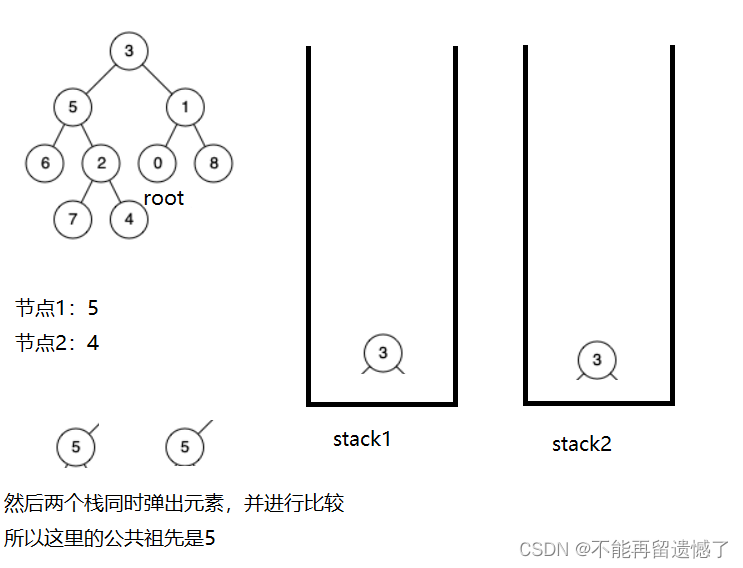
第二种方法我们可以借用栈这种数据结构来解决,我们可以将从根节点到这两个节点路径上的节点分别放在两个栈中。然后得到了两个栈之后,我们比较栈中元素的大小,将栈中元素较大的站里面的元素弹出部分,使两个栈中的元素数量相等,接着我们就同时弹出两个栈中的元素并进行比较,如果相等就说明这个节点就是最近公共祖先。
但是我们怎样准确的将从根节点到该节点路径上的节点存放在栈中呢?
就像这个例子,我们需要找到节点5和节点4的公共祖先。
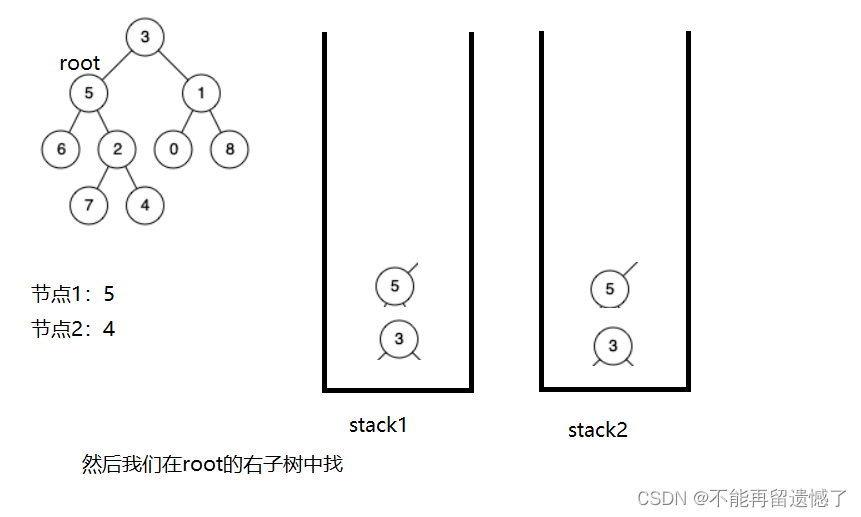
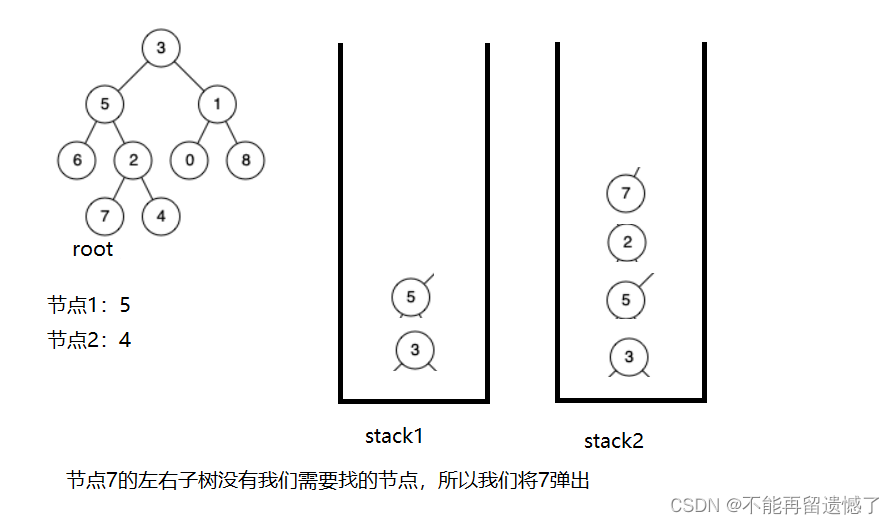
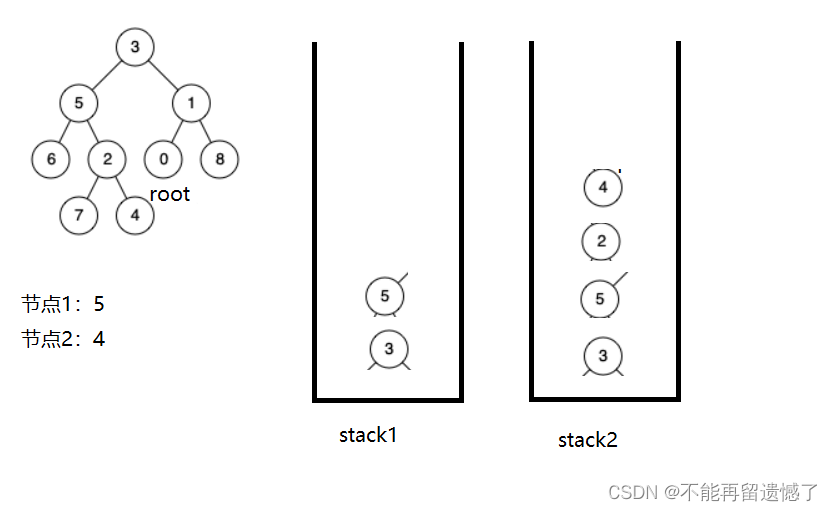
当我们找节点5路径上的节点时很容易找到,但是4呢?我们知道从根节点到节点4的路径的节点有3,5,2,4,但是我们怎样做才能不把6和7也算上呢?我们这样,当我们遍历完了5这个节点的左子树时,如果该节点的左子树或者右子树没有找到我们要找的两个节点,我们就将该左子树或者右子树上的节点从栈中弹出,最后栈中就只有从根节点到需要找的节点路径上的节点了。
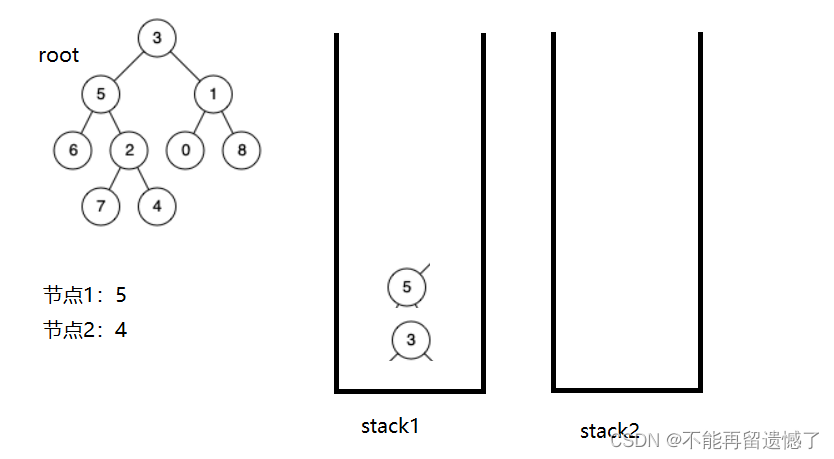
代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Deque<TreeNode> stack1 = new ArrayDeque<>();
Deque<TreeNode> stack2 = new ArrayDeque<>();
lowestCommonAncestorChild(root,p,stack1);
lowestCommonAncestorChild(root,q,stack2);
int len = stack1.size() - stack2.size();
if(len < 0) {
len = -len;
while(len > 0) {
stack2.pop();
len--;
}
}else {
while(len > 0) {
stack1.pop();
len--;
}
}
while(!stack1.isEmpty()) {
if(stack1.peek() == stack2.peek()) {
return stack1.peek();
}
stack1.pop();
stack2.pop();
}
return null;
}
private boolean lowestCommonAncestorChild(TreeNode root,TreeNode node,Deque stack) {
if(root == null) {
return false;
}
stack.push(root);
if(root == node) {
return true;
}
boolean ret1 = lowestCommonAncestorChild(root.left,node,stack);
//当我们在该节点的左树中找到了需要找的节点,说明该节点不需要弹出,
//我们直接返回,节省时间
if(ret1 == true) {
return true;
}
boolean ret2 = lowestCommonAncestorChild(root.right,node,stack);
if(ret2 == true) {
return true;
}
//当该节点的左树和右树都没有时,我们就需要弹出该节点
stack.pop();
return false;
}
}
根据二叉树创建字符串
根据二叉树创建字符串(难度:简单)
题目要求
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 “()” 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
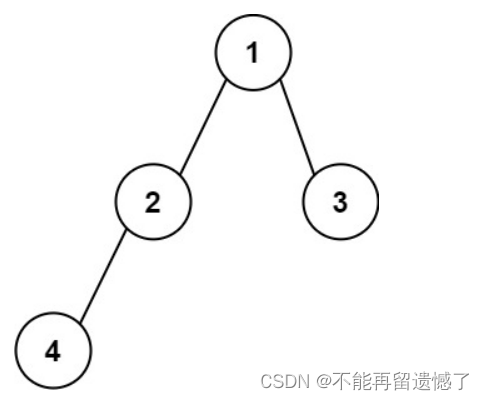
输入:root = [1,2,3,4]
输出:“1(2(4))(3)”
解释:初步转化后得到 “1(2(4)())(3()())” ,但省略所有不必要的空括号对后,字符串应该是"1(2(4))(3)" 。
示例 2:
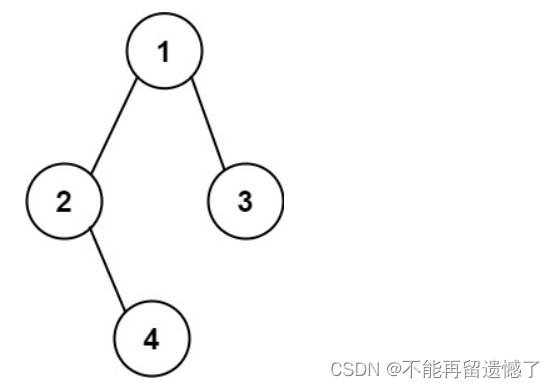
输入:root = [1,2,3,null,4]
输出:“1(2()(4))(3)”
解释:和第一个示例类似,但是无法省略第一个空括号对,否则会破坏输入与输出一一映射的关系。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public String tree2str(TreeNode root) {
}
}
做题思路
根据实例我们可以知道,当根节点的左树和右树不为null时,我们需要在添加节点之前加入一个
“(”,当左树或者右树遍历完之后我们加上")“。当左树不为null时,我们正常进行遍历;当左树为null,右树不为null时,我们需要添加”()",然后再遍历右子树,当右树不为null时,我们正常加
“(“和”)”,当右树为null时,什么都不需要做。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public String tree2str(TreeNode root) {
StringBuilder str = new StringBuilder();
tree2strChild(root,str);
return str.toString();
}
public void tree2strChild(TreeNode root,StringBuilder str) {
if(root == null) {
return;
}
str.append(root.val);
if(root.left != null) {
str.append("(");
tree2strChild(root.left,str);
str.append(")");
}else {
if(root.right != null) {
str.append("()");
}else {
return;
}
}
if(root.right != null) {
str.append("(");
tree2strChild(root.right,str);
str.append(")");
}else {
return;
}
}
}