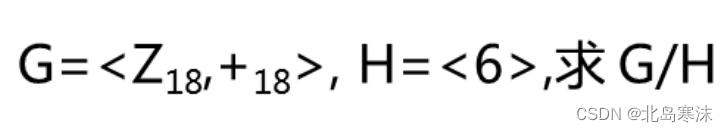一开始想的是分类讨论，看那条边加了之后成不成环，如果不成环且权值在前n-1，则一定在MST里，不在前n-1则不在MST里；如果成环了，如果权值不在前n-1，则不在MST里，如果权值在前n-1，则需要判断环中其余边是不是都<wi，如果是，则在MST里面，否则就不在

然后问题就在于，怎么看环中其余边是不是都<wi

有两个想法：

一个是dfs遍历环统计最大值，但是考虑到最坏情况复杂度为NQ，因此不可能这么做

一个是维护树链RMQ，可能要用树剖来写，但是我不会QwQ

事实上这也是做法之一，但是不需要这么麻烦

题意：

有一个图，它有MST，对于每次询问都问是否能加一条边，使得该边在新图的MST中，如果是输出Yes，否则就是No

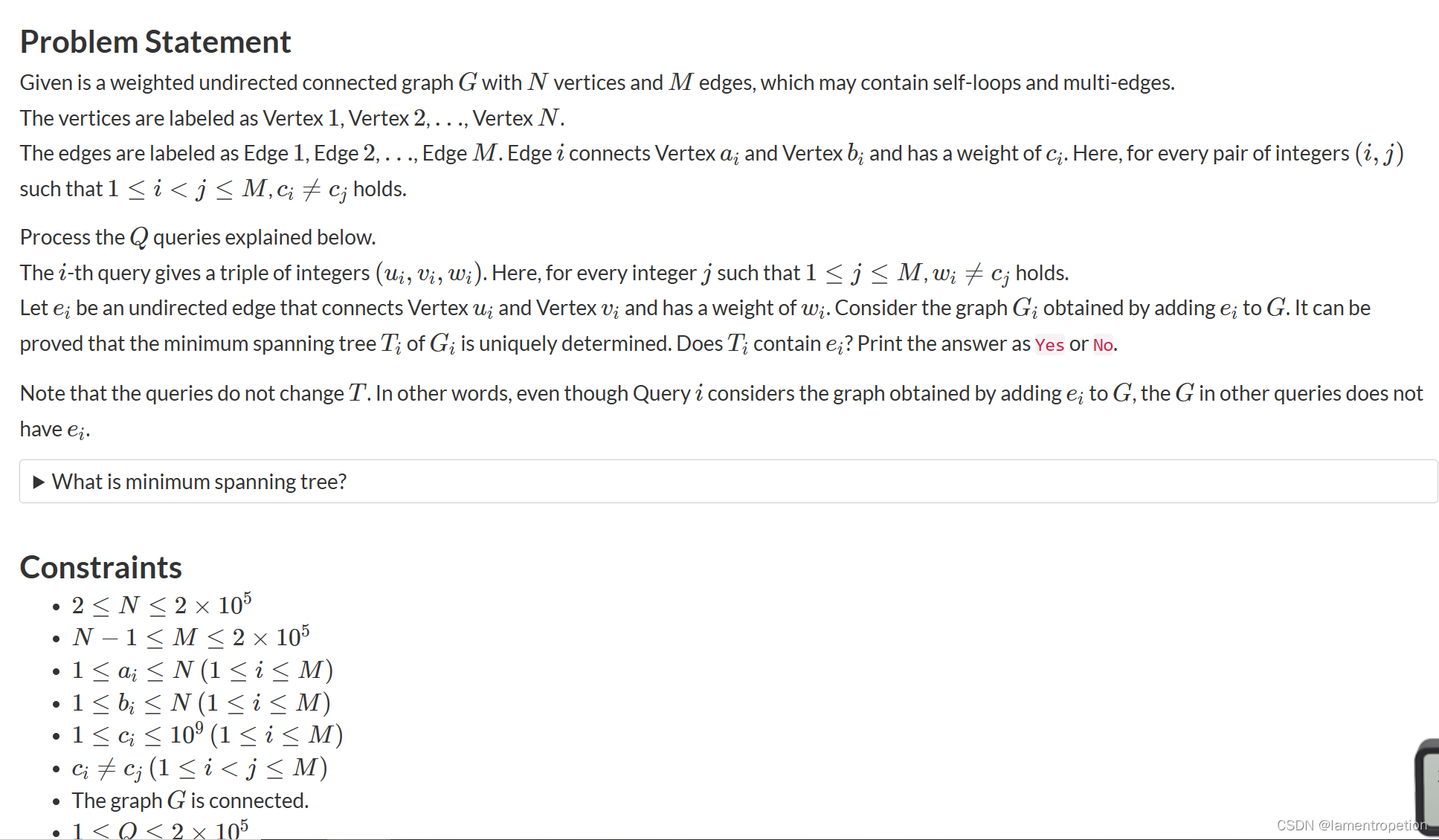
 思路：

考虑将原边和查询边一起参与Kruskal的过程

如果是原边，则直接加入

如果是查询边，则直接看是否成环即可

为什么，因为它是从小到大加边的，所以此时如果成环了，环内其余边都<=wi，就不需要树链RMQ了

感觉将查询边一起参与Kruskal的过程很帅啊

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=2e5+10;
const int mxe=2e5+10;

struct ty{
	int u,v,w,id;
}e[mxe<<2];

int N,M,Q,a,b,c;
int f[mxn],ans[mxn];

int find(int x){
	return f[x]=(x==f[x])?x:find(f[x]);
}
void join(int u,int v){
	int f1=find(u),f2=find(v);
	if(f1!=f2) f[f1]=f2;
}
bool cmp(ty x,ty y){
	return x.w<y.w;
}
void solve(){
	cin>>N>>M>>Q;
	for(int i=1;i<=N;i++) f[i]=i; 
	for(int i=1;i<=M;i++){
		cin>>a>>b>>c;
		e[i]={a,b,c,0};
	} 
	for(int i=1;i<=Q;i++){
		cin>>a>>b>>c;
		e[M+i]={a,b,c,i};
	}
	sort(e+1,e+1+M+Q,cmp);
	for(int i=1;i<=M+Q;i++){
		if(e[i].id==0) join(e[i].u,e[i].v);
		else{
			if(find(e[i].u)!=find(e[i].v)) ans[e[i].id]=1;
			else ans[e[i].id]=0;
		}
	}
	for(int i=1;i<=Q;i++){
		if(ans[i]) cout<<"Yes"<<'\n';
		else cout<<"No"<<'\n';
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int __=1;//cin>>__;
	while(__--)solve();return 0;
}