文章目录
- (简单)35. 搜索插入位置
- (*中等)34. 在排序数组中查找元素的第一个和最后一个位置
- (简单,常见面试题)69. x的平方根
- (简单) 367. 有效的完全平方数
# (简单)704. 二分查找
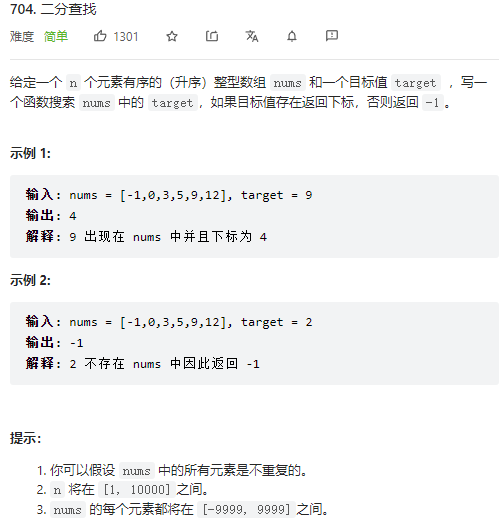
题目链接
代码随想录 - 二分查找思路
二分查找,思路很简单,但是在while循环left和right的比较是写<=还是<,还有right=mid还是right=mid-1容易混淆
需要想清楚对区间的定义,是[left,right],还是[left,right)


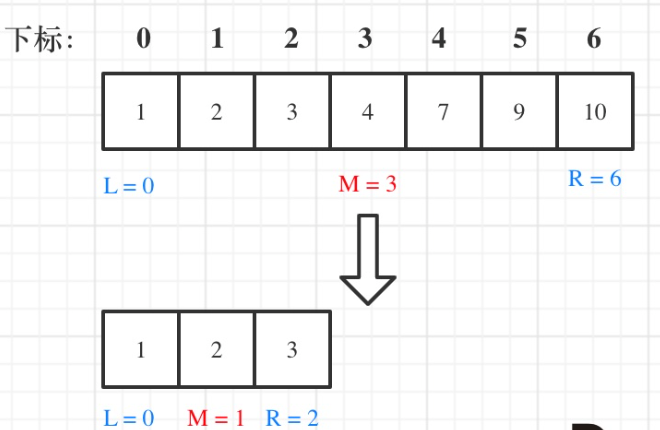

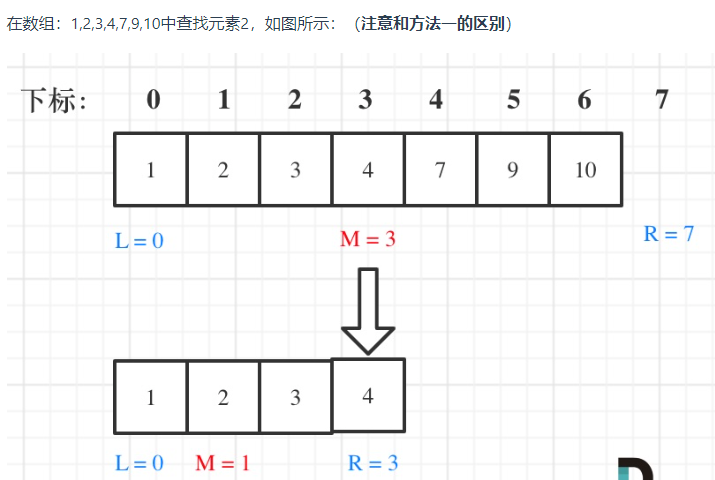
(版本一,左闭右闭版本)
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int mid;
while (left <= right) {
mid = left + ((right-left)/2);//防止溢出
if (nums[mid] == target) {
return mid;
}
if (target > nums[mid]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
}
(版本二,左闭右开)
class Solution {
public int search(int[] nums, int target) {
//避免当target小于nums[0] 或者大于 nums[nums.length-1]时 多次循环
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
int left = 0;
int right = nums.length;
int mid;
while (left < right) {
mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}
if (target > nums[mid]) {
left = mid + 1;
} else {
right = mid;
}
}
return -1;
}
}
(简单)35. 搜索插入位置
题目链接

class Solution {
public int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int mid;
while (left <= right) {
mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}
if (target > nums[mid]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return left;//right+1
}
}
(*中等)34. 在排序数组中查找元素的第一个和最后一个位置

题目链接
我的思路:按照传统二分查找的方式,找到等于target的数组的下标,然后向两边扩展,如果没找到直接返回[-1,-1]
class Solution {
public int[] searchRange(int[] nums, int target) {
//如果数组长度是0,则不用判断
if (nums == null || nums.length == 0) {
return new int[]{-1, -1};
}
//如果target的值小于第一个元素或者大于最后一个元素,也不用判断
if ((target < nums[0]) || (target > nums[nums.length - 1])) {
return new int[]{-1, -1};
}
int res = search(nums, target);
if (res == -1) {
return new int[]{-1, -1};
}
int left = res;
int right = res;
while ((left >= 0) && (nums[left] == nums[res])) {
left--;
}
while ((right < nums.length) && (nums[right] == nums[res])) {
right++;
}
return new int[]{left + 1, right - 1};
}
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int mid;
while (left <= right) {
mid = left + ((right - left) >> 1);
if (target == nums[mid]) {
return mid;
}
if (target > nums[mid]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
}
看了官方的解题思路,是找出数组中【第一个等于target的位置(leftIdx)】和【第一个大于target的位置减一(rightIdx)】
二分查找中
- 寻找leftIdx即为在数组中寻找第一个大于等于 target的下标
- 寻找rightIdx即为在数组中寻找第一个大于 target的下标,然后减一
二者的判断条件不同,为了代码的复用,定义一个函数,其中包含布尔类型的lower参数,该参数为true时,则查找第一个大于等于target的下标,该参数为false时,则查找第一个大于target的下标
最后,因为target可能不在数组中,因此需要重新校验两个下标leftIdx和rightIdx,看是否符合条件,如果符合,就返回[leftIdx,rightIdx],不符合就返回[-1,-1]

class Solution {
public int[] searchRange(int[] nums, int target) {
//如果数组长度是0,则不用判断
if (nums == null || nums.length == 0) {
return new int[]{-1, -1};
}
//如果target的值小于第一个元素或者大于最后一个元素,也不用判断
if ((target < nums[0]) || (target > nums[nums.length - 1])) {
return new int[]{-1, -1};
}
int leftIdx = search(nums, target, true);
int rightIdx = search(nums, target, false) - 1;
if (leftIdx >= 0 && rightIdx < nums.length && leftIdx <= rightIdx && nums[leftIdx] == target && nums[rightIdx] == target) {
return new int[]{leftIdx, rightIdx};
}
return new int[]{-1, -1};
}
public int search(int[] nums, int target, boolean lower) {
int left = 0;
int right = nums.length - 1;
int mid;
int ans = nums.length;
while (left <= right) {
mid = left + ((right - left) >> 1);
//说明当前的mid所在的值比target大,需要缩小范围
//找leftIdx,如果target小于nums[mid],缩小范围
//如果target==nums[mid],也要缩小范围,但是会记录mid
//找rightIdx,只要target<nums[mid],缩小范围
if (target < nums[mid] || (lower && target == nums[mid])) {
right = mid - 1;
ans = mid;
} else {
//找rightIdx,只要target < nums[mid] 不成立
//也就是target=nums[mid]或者target>nums[mid] left都会变化
left = mid + 1;
}
}
return ans;
}
}
(简单,常见面试题)69. x的平方根

我的思路,将x的值赋给tmp,将tmp不断除以2
记录下面两个数,在这两个数之间使用二分查找:
- 使得tmp^2小于x的最大的tmp值
- 使得tmp^2大于x的最小的tmp值
class Solution {
public int mySqrt(int x) {
if (x == 0 || x == 1) {
return x;
}
int pre = x;
int tmp = x / 2;
while (tmp > x / tmp) { //原来是 tmp * tmp > x
pre = tmp;
tmp /= 2;
}
if (tmp == x / tmp) { //原来是 tmp * tmp == x
return tmp;
}
//pre和tmp之间找到答案,缩小范围
return search(x, tmp, pre);
}
public int search(int x, int tmp, int pre) {
int left = tmp;
int right = pre;
int mid;
int ans = tmp;
while (left <= right) {
mid = left + ((right - left) >> 1);
if (mid == x / mid) { //原来是 mid * mid == x
return mid;
}
if (mid > x / mid) { // 原来是mid * mid > x
right = mid - 1;
} else {
ans = mid;
left = mid + 1;
}
}
return ans;
}
}
官网解答,笔记:
在不使用 x \sqrt{x} x函数的情况下,得到x的平方根的整数部分。一般的思路有以下几种:
- 通过其它的数学函数代替平方根函数得到精确结果,取整数部分作为答案
- 通过数学方法得到近似结果,直接作为答案
方法一 袖珍计算器算法
【袖珍计算器算法】是一种用指数函数exp和对数函数ln代替平方根函数的方法。通过有限的、可以使用的数学函数,得到想要的结果。
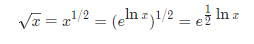
当x=2147395600时,
e
1
2
ln
x
e^{\frac{1}{2}\ln x}
e21lnx的计算结果与正确值46340相差
1
0
−
11
10^{-11}
10−11,这样在对结果取整数部分时,会得到46339这个错误结果。
因此,在得到结果的整数部分ans后,应该找出ans与ans+1中哪一个是真正的答案。
class Solution {
public int mySqrt(int x) {
if (x == 0 || x == 1) {
return x;
}
int ans = (int) Math.exp(0.5 * Math.log(x));
return (long) (ans + 1) * (ans + 1) > x ? ans : ans + 1;
}
}
方法二 二分查找
由于x平方根的整数部分ans是满足 k 2 ≤ x k^2 \leq x k2≤x的最大k值,因此可以对k进行二分查找,从而得到答案
二分查找的下界是1,上界可以粗略的=地设定为x。在二分查找中的每一步中,我们只需要比较中间元素mid的平方与x的大小关系,并通过比较的结果调整上下界的范围。由于我们所有的运算都是整数运算,所以,不会存在误差,因此在得到最终的答案ans后,也就不需要再去尝试ans+1了。
class Solution {
public int mySqrt(int x) {
if (x == 0 || x == 1) {
return x;
}
int left = 1;
int right = x;
int mid;
int ans = -1;
while (left <= right) {
mid = left + ((right - left) >> 1);
if ((long) mid * mid == x) {
return mid;
}
if ((long) mid * mid < x) {
ans = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return ans;
}
}
(简单) 367. 有效的完全平方数

二分查找
class Solution {
public boolean isPerfectSquare(int num) {
if (num == 1) {
return true;
}
int left = 1;
int right = num;
int mid;
while (left <= right) {
mid = left + ((right - left) >> 1);
if ((long) mid * mid == num) {
return true;
}
if ((long) mid * mid < num) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return false;
}
}
当然还可以使用内置的库函数
根据完全平方数的性质,只需要判断num的平方根x是否为整数即可。
class Solution {
public boolean isPerfectSquare(int num) {
int x = (int) Math.sqrt(num);
return x * x == num;
}
}
还有暴力法
如果num为完全平方数,那么一定存在正整数x满足x * x = num。于是,可以从1开始遍历所有的正整数,一直遍历到46340即可,因为 2 31 − 1 ≈ 46340 \sqrt{2^{31}-1} \approx 46340 231−1≈46340
class Solution {
public boolean isPerfectSquare(int num) {
if (num == 1) {
return true;
}
for (int i = 2; i <= 46340; i++) {
if (i * i > num) {
break;
}
if (i * i == num) {
return true;
}
}
return false;
}
}