文章目录
- 基本概念
- 1.正规子群
- 2.商群
- 常见题型
- 1.正规子群的判定和证明
- 2.给定群和正规子群,求商群
基本概念
1.正规子群
正规子群的定义:设<G,※>是群,H是G的子群。如果对于G中的任意元素g,都有gH=Hg,则称H是G的正规子群或不变子群。
平凡的正规子群和单群:
- 平凡的正规子群:任何群都有两个平凡的正规子群,分别是只含有幺元的子群和其本身。
- 单群的定义:如果一个群只有平凡的正规子群,且该群不是只含有幺元的群,那么这个群就被称为单群。
交换群和正规子群的关系:如果一个群是交换群,那么这个群的所有子群都是正规子群。
其他相关结论:
- 正规子群的共享性:假设H和K都是G的子群,如果H是G的正规子群且H包含于K,那么H也是K的正规子群。
- 正规子群与陪集的关系:
- 任意元素的左右陪集相等:一个子群是正规子群当且仅当对于群中的任意元素,该元素作为代表元素时的左陪集和右陪集始终相等。
- 正规子群的指数判别定理:设G为群,H是G的子群。如果H在G中的指数为2,则H是G的正规子群。也就是说,如果子群形成的陪集个数为2,那么这个子群一定是正规子群。
- 有限正规子群的阶数判别法:对于有限群来说,如果子群的阶数是群的阶数的一半,那么这个子群一定是正规子群。
- 交错群和对称群的关系:相同阶数的交错群是对称群的正规子群。
正规子群的基本性质:
设H是G的子群,则以下几个命题是相互等价的:
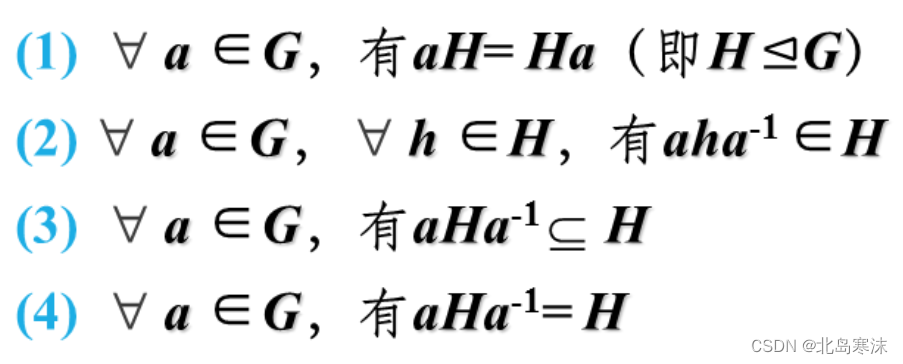
正规子群的简单性质:
- 两个正规子群的情况:设G是一个群,H1和H2是G的正规子群。那么H1和H2的交集以及H1※H2仍然是G的正规子群。
- 一个正规子群和一个子群的情况:设G是一个群,H1是G的正规子群,H2是G的子群。则H1与H2的交集是B的正规子群,AB是G的子群。
正规子群不具有传递性:如果A是B的正规子群,B是C的正规子群,A也不一定是C的正规子群。
2.商群
商群的定义:设G是群,H是G的一个正规子群。H在G上的所有陪集组成的集合,以及陪集的乘法运算构成一个群,这个群被称为G的商群。
- 陪集的乘法运算:设两个陪集分别为aH和bH,则陪集的乘法运算为:aH※bH=(ab)H。
对商群的理解:只要给定一个群和对应的正规子群,就可以确定一个商群。
商群的性质:
- 商群中的单位元:商群中的单位元即为对应的正规子群(eH)。
- 商群和交换群的关系:假设G是一个交换群,H是G的子群,那么商群G/H也是一个交换群。
- 商群的阶数和群的阶数的关系:有限群G的商群的阶是群的阶数的因子。
- 商群和循环群的关系:假设G是一个循环群,H是G的子群,那么商群G/H也是一个循环群。
商群的性质比原先的群更简单。通过讨论商群的性质,可以部分了解原先的群的性质。
常见题型
1.正规子群的判定和证明
题型概述:对于一个给定的群,再另给出一个代数系统,判断这个代数系统是否是给定的群的正规子群。
可用的证明方法:
- 通过定义证明:首先判定这个代数系统是另一个代数系统的子群,再根据定义判断这个代数系统是另一个代数系统的正规子群即可。
- 通过性质证明:一般是使用第二条性质进行证明。这是因为通过定义证明时需要判断两个集合相等,而使用性质证明则只需要判断一个元素是否属于一个集合即可,一般情况下更加简单。
例题1:

解析:本题考查正规子群的判定,本题可用采用定义进行证明。
首先判定H是G的子群。这里可以通过子群的判定定理三(对H中的任意元素a和b,a※b-1仍然是H的元素)来判定H是G的子群(二阶矩阵求逆比较简单,可以通过待定系数法做)。
接着判定这个子群是正规子群。只需假设G中的任意元素g,判定gH=Hg即可。具体来说,判定这两个集合相等只需要判断这两个集合相互包含即可。具体过程如下:
另外,本题也可以通过正规子群的性质(第二条)进行证明,这样的过程更加简单,这是因为证明元素属于集合的难度是比证明两个集合相等的难度更小的,在此不再赘述。
例题2:

解析:本题考查正规子群的判定,仍然可以直接使用定义进行判定。
首先证明H是K的子群,可以根据子群的传递性质简单判定。
接着证明H是K的正规子群,只需要按照定义进行证明即可,具体过程如下:
例题3:

解析:本题考查正规子群的判定,仍然按照定义进行判定即可。由于题目中已经说明了H是S3的子群,因此只需要进行正规子群的判定过程即可。
首先求出子群H的所有陪集。找出S3中的所有元素,分别作为左运算数和右运算数进行运算,即可求出所有左陪集和右陪集。
接着判定是否所有左右陪集都相等。逐一进行比较判断即可。
同时通过本题也可以总结出陪集和正规子群的关系:一个子群是正规子群当且仅当对于群中的任意元素,该元素作为代表元素时的左陪集和右陪集始终相等。
具体的求解过程如下:
例题4:
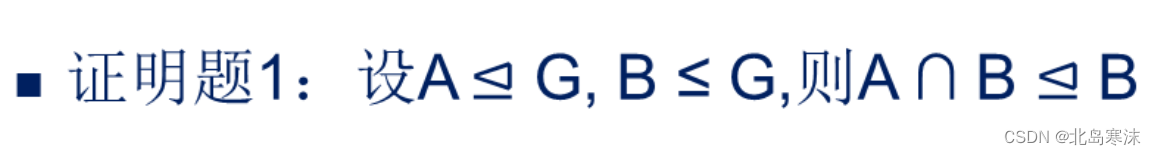
解析:本题考查正规子群的证明,最简单的方法是通过性质进行证明。
具体过程如下:
这里使用到的技巧是:为了证明一个元素属于两个集合的交集,只需要证明这个元素分别属于这两个集合即可。
例题5:

解析:本题考查正规子群的证明,需要分别证明必要性和充分性,有一定的难度。
具体求解过程如下:
例题6:证明下面的定理:

解析:本题考查正规子群的判定,仍然可以通过正规子群的基本性质中的第二条进行判定。
具体的证明过程如下所示:
2.给定群和正规子群,求商群
题型概述:题目中给出指定的群和对应的正规子群,需要求出这个正规子群对应的商群。
求解方法:首先明确群和对应的正规子群,接着只需要对于群中的每一个元素求对应该正规子群的陪集即可,所有的陪集就构成了商群。
例题1:
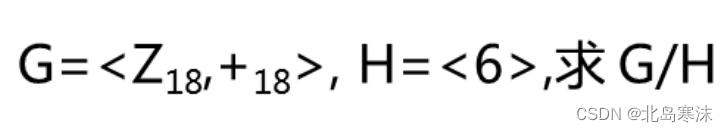
解析:本题考查在给定群和正规子群的情况下求商集,直接根据定义求解即可。
这里的H=< 6 >表示H={0,6,12}。在模18加法的意义下,所有陪集构成的商群为:G/H={{0,6,12},{1,7,13},{2,8,14},{3,9,15},{4,10,16},{5,11,17}}。