文章目录
- 二范数
- F范数
- 核范数
- 无穷范数
- L1范数
- L2范数
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。
范数是一种数学概念,可以将向量或矩阵映射到非负实数上,通常被用来衡量向量或矩阵的大小或距离。在机器学习和数值分析领域中,范数是一种重要的工具,常用于正则化、优化、降维等任务中。
本文以torch.linalg.norm()函数举例,详细讲解F范数、核范数、无穷范数等范数的定义和计算。
参考官方文档https://pytorch.org/docs/stable/generated/torch.linalg.norm.html
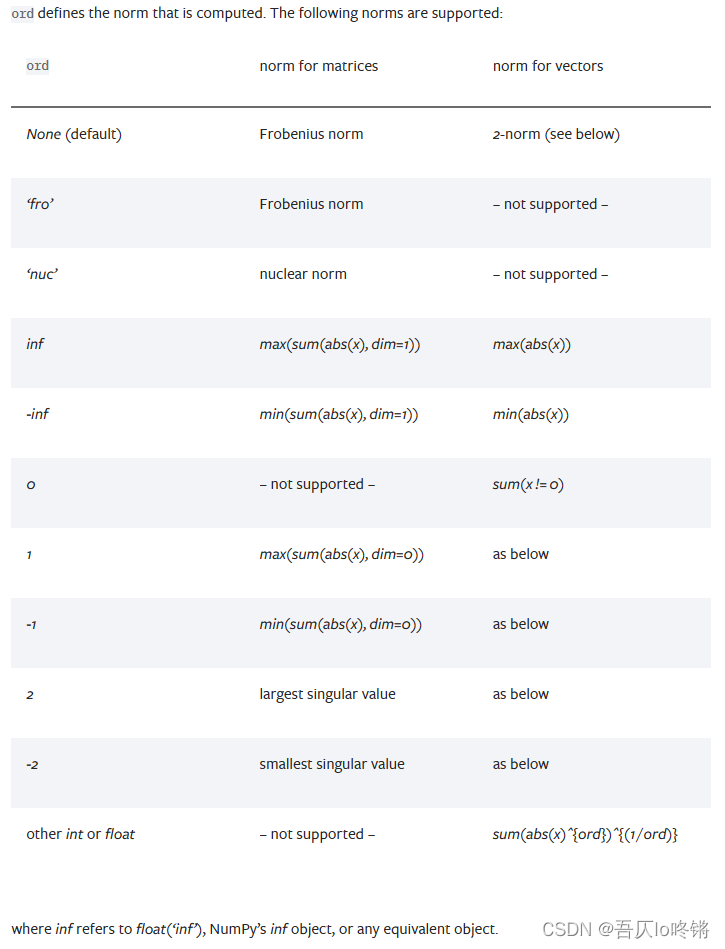
由于torch.norm()已弃用,所以以torch.linalg.norm()讲解,也可以使用 NumPy 或者 SciPy 库中的 numpy.linalg.norm 或 scipy.linalg.norm 函数。下图是其支持的各种范数:
二范数
标准二范数(2-norm)是向量的一种范数,通常用来衡量向量的大小。二范数可以说是出场率最高的了,比如在最小二乘法中,还有如线性代数中的向量空间、矩阵分解等。
标准二范数的一些重要性质包括:
- 非负性:
对于任意向量 x x x,它的标准二范数都是非负的,即 ∣ ∣ x ∣ ∣ 2 ≥ 0 ||x||_2 \geq 0 ∣∣x∣∣2≥0。 - 齐次性:
对于任意向量 x x x和任意实数 k k k,有 ∣ ∣ k x ∣ ∣ 2 = ∣ k ∣ ∣ ∣ x ∣ ∣ 2 ||kx||_2 = |k|||x||_2 ∣∣kx∣∣2=∣k∣∣∣x∣∣2。 - 三角不等式:
对于任意向量 x 和 y,有 ∣ ∣ x + y ∣ ∣ 2 ≤ ∣ ∣ x ∣ ∣ 2 + ∣ ∣ y ∣ ∣ 2 ||x+y||_2\leq ||x||_2+||y||_2 ∣∣x+y∣∣2≤∣∣x∣∣2+∣∣y∣∣2。 - 向量的 Cauchy-Schwarz 不等式:
对于任意向量 x x x和 y y y,有 ∣ x ⋅ y ∣ ≤ ∣ ∣ x ∣ ∣ 2 ∣ ∣ y ∣ ∣ 2 |x·y| \leq ||x||_2 ||y||_2 ∣x⋅y∣≤∣∣x∣∣2∣∣y∣∣2。
对于一个
n
n
n维向量
x
x
x,它的标准二范数定义如下:
∣
∣
x
∣
∣
2
=
(
∑
i
=
1
n
x
i
2
)
1
2
||x||_2 = (\sum_{i=1}^n x_i^2)^{\frac{1}{2}}
∣∣x∣∣2=(i=1∑nxi2)21
其中,
x
i
x_i
xi表示向量
x
x
x的第
i
i
i个元素的值。
标准二范数的计算方法类似于欧几里得距离,都是将所有元素的平方和开根号。标准二范数也可以表示为向量的点积和向量的模长的乘积,即:
∣
∣
x
∣
∣
2
=
x
⋅
x
=
∣
x
∣
x
∣
x
∣
⋅
x
∣
x
∣
||x||_2 = \sqrt{x·x}= |x|\sqrt{\frac{x}{|x|}·\frac{x}{|x|}}
∣∣x∣∣2=x⋅x=∣x∣∣x∣x⋅∣x∣x
其中, ⋅ · ⋅表示点积, ∣ x ∣ |x| ∣x∣表示向量 x x x的模长, x ∣ x ∣ \frac{x}{|x|} ∣x∣x表示向量 x x x的单位向量。
在 PyTorch 中,可以使用 torch.linalg.norm 函数来计算向量的标准二范数,例如:
x = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)
norm_2 = torch.linalg.norm(x)
print(norm_2)
# 输出 7.4162,即 (√(1^2 + 2^2 + 3^2 + 4^2 + 5^2))
F范数
F范数(Frobenius范数)是一种矩阵的范数,用来衡量矩阵的大小。F范数在很多应用中都有重要的作用,例如矩阵近似、矩阵压缩、矩阵分解等。
F范数的一些重要性质包括:
- 非负性
对于任意矩阵 A A A,它的F范数都是非负的,即 ∣ ∣ A ∣ ∣ F ≥ 0 ||A||_F\geq 0 ∣∣A∣∣F≥0。 - 齐次性
对于任意矩阵 A A A和任意实数 k k k,有 ∣ ∣ k A ∣ ∣ F = ∣ k ∣ ∣ ∣ A ∣ ∣ F ||kA||_F = |k|||A||_F ∣∣kA∣∣F=∣k∣∣∣A∣∣F。 - 三角不等式
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A + B ∣ ∣ F ≤ ∣ ∣ A ∣ ∣ F + ∣ ∣ B ∣ ∣ F ||A+B||_F\leq ||A||_F + ||B||_F ∣∣A+B∣∣F≤∣∣A∣∣F+∣∣B∣∣F。 - 特殊性质
对于一个正交矩阵 Q Q Q,它的F范数等于 1,即 ∣ ∣ Q ∣ ∣ F = 1 ||Q||_F=1 ∣∣Q∣∣F=1。
对于一个 n n n行 m m m列的矩阵 A A A,它的F范数定义如下:
∣ ∣ A ∣ ∣ F = ( ∑ i = 1 n ∑ j = 1 m A i j 2 ) 1 2 ||A||_F = (\sum_{i=1}^n\sum_{j=1}^mA_{ij}^2)^{\frac{1}{2}} ∣∣A∣∣F=(i=1∑nj=1∑mAij2)21
其中,
A
i
j
A_{ij}
Aij表示矩阵
A
A
A的第
i
i
i行第
j
j
j列元素的值。
F范数的计算方法类似于标准二范数,都是将所有元素的平方和开根号。与标准二范数不同的是,F范数的加和是在矩阵的所有元素上进行的,而不是在向量的所有元素上进行的。
在 PyTorch 中,可以使用 torch.linalg.norm 函数来计算矩阵的F范数,其对应的参数为 ord='fro',例如:
A = torch.tensor([[1, 2],
[3, 4],
[5, 6]], dtype=torch.float)
norm_F = torch.linalg.norm(A, ord='fro')
print(norm_F)
# 输出 9.5394,即 (√(1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2))
核范数
核范数(nuclear norm),也称为矩阵1-范数(matrix 1-norm),也是一种用于衡量矩阵的大小的范数。核范数在矩阵分解、矩阵压缩、矩阵近似等方面有广泛的应用。例如在矩阵分解中,核范数可以用于衡量原始矩阵与分解后的矩阵的差异程度,从而可以优化分解的结果。
核范数的一些重要性质包括:
- 非负性:
对于任意矩阵 A A A,它的核范数都是非负的,即 ∣ ∣ A ∣ ∣ ∗ ≥ 0 ||A||_* \geq 0 ∣∣A∣∣∗≥0。 - 齐次性:
对于任意矩阵 A A A和任意实数 k k k,有 ∣ ∣ k A ∣ ∣ ∗ = ∣ k ∣ ∣ ∣ A ∣ ∣ ∗ ||kA||_* = |k| ||A||_* ∣∣kA∣∣∗=∣k∣∣∣A∣∣∗。 - 子加性:
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A + B ∣ ∣ ∗ ≤ ∣ ∣ A ∣ ∣ ∗ + ∣ ∣ B ∣ ∣ ∗ ||A+B||_* \leq ||A||_* + ||B||_* ∣∣A+B∣∣∗≤∣∣A∣∣∗+∣∣B∣∣∗。 - 矩阵的谱范数性质:
对于任意矩阵 A A A,有 ∣ ∣ A ∣ ∣ ∗ = ∣ ∣ A T ∣ ∣ ∗ = ∣ ∣ A H ∣ ∣ ∗ ||A||_* = ||A^T||_* = ||A^H||_* ∣∣A∣∣∗=∣∣AT∣∣∗=∣∣AH∣∣∗,其中 A H A^H AH是矩阵 A A A的共轭转置。
对于一个矩阵
A
A
A,它的核范数定义如下:
∣
∣
A
∣
∣
∗
=
∑
i
σ
i
||A||_* = \sum_i\sigma_i
∣∣A∣∣∗=i∑σi
其中, σ i \sigma_i σi是矩阵 A A A的奇异值(singular value),表示矩阵 A A A的第 i i i大的奇异值。核范数的计算方法是将矩阵 A 奇异值的绝对值相加。
奇异值分解(singular value decomposition,SVD)是一种常用的矩阵分解方法,用于将一个矩阵分解为三个矩阵的乘积,即
A
=
U
Σ
V
T
A = UΣVᵀ
A=UΣVT
具体求解这里不过多展开,可以理解为一种压缩分解技术,原本很大的矩阵,现在只需3个小矩阵就能存储,可以使用torch.svd()进行奇异值分解。
在 PyTorch 中,可以使用 torch.linalg.norm 函数来计算矩阵的核范数,其对应的参数为 ord='nuc',例如:
A = torch.tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype=torch.float)
norm_nuclear = torch.linalg.norm(A, ord='nuc')
u, s, v = torch.svd(A)
print(s)
print(norm_nuclear)
# 输出 17.9165,即 1.6848e+01 + 1.0684e+00 + 2.3721e-07

注:不同函数封装的奇异值分解算法可能不同,得到奇异值可能有些许出入,但应都在一个数量级。
(
插播反爬信息)博主CSDN地址:https://wzlodq.blog.csdn.net/
无穷范数
无穷范数是矩阵的一种范数,也称为最大值范数或者列范数。无穷范数在矩阵计算和优化中有广泛的应用。例如,在矩阵乘法中,可以使用无穷范数来衡量矩阵乘积的大小;在优化问题中,可以使用无穷范数作为约束条件或者目标函数。
无穷范数也有一些重要的性质,包括:
- 非负性
对于任意矩阵 A A A,它的无穷范数都是非负的,即 ∣ ∣ A ∣ ∣ ∞ ≥ 0 ||A||_\infty \geq 0 ∣∣A∣∣∞≥0。 - 齐次性
对于任意矩阵 A A A和任意实数 k k k,有 ∣ ∣ k A ∣ ∣ ∞ = ∣ k ∣ ∣ ∣ A ∣ ∣ ∞ ||kA||_\infty = |k| ||A||_\infty ∣∣kA∣∣∞=∣k∣∣∣A∣∣∞。 - 三角不等式
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A + B ∣ ∣ ∞ ≤ ∣ ∣ A ∣ ∣ ∞ + ∣ ∣ B ∣ ∣ ∞ ||A+B||_\infty \leq ||A||_\infty + ||B||_\infty ∣∣A+B∣∣∞≤∣∣A∣∣∞+∣∣B∣∣∞。 - 矩阵乘法性质
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A B ∣ ∣ ∞ ≤ ∣ ∣ A ∣ ∣ ∞ ∣ ∣ B ∣ ∣ ∞ ||AB||_\infty \leq ||A||_\infty ||B||_\infty ∣∣AB∣∣∞≤∣∣A∣∣∞∣∣B∣∣∞。
对于一个 m × n m\times n m×n的矩阵 A A A,它的无穷范数定义为:
∣ ∣ A ∣ ∣ ∞ = max 1 ≤ i ≤ m ∑ j = 1 n ∣ a i j ∣ ||A||{\infty} = \max_{1\leq i\leq m} \sum_{j=1}^{n} |a_{ij}| ∣∣A∣∣∞=1≤i≤mmaxj=1∑n∣aij∣
其中, i i i的取值范围是 [ 1 , m ] [1, m] [1,m],表示矩阵 A A A的第 i i i行; j j j的取值范围是 [ 1 , n ] [1, n] [1,n],表示矩阵 A A A的第 j j j列。换句话说,无穷范数是将每一列的绝对值相加,然后取其中的最大值。
PyTorch 中其对应的参数为ord='inf',例如:
A = torch.tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype=torch.float)
norm_inf = np.linalg.norm(A, ord=np.inf)
print(norm_inf)
# 输出 24,即 max{1+2+3, 4+5+6, 7+8+9}
同理,ord='-inf'表示取最小值。
需要注意的是,计算矩阵的无穷范数比计算其他范数更加简单和快速,因为只需要对每一列的绝对值相加,然后取其中的最大值即可。
L1范数
L1 范数(L1 norm)是指向量中各个元素的绝对值之和,也称为曼哈顿距离(Manhattan distance)或城市街区距离(city block distance)。
L1 范数可以被用于衡量向量或矩阵中各个元素的绝对大小,具有一些特殊的性质,例如对于稀疏向量,它的 L1 范数更容易被最小化,因为它倾向于将向量的一些元素设为 0。
与无穷范数类似,L1 范数也具有一些重要的性质,包括非负性、齐次性、三角不等式和矩阵乘法性质。在矩阵计算和优化中,L1 范数也有广泛的应用。例如,在稀疏信号处理中,可以使用 L1 范数来促进信号的稀疏性;在机器学习中,可以使用 L1 范数作为正则化项来防止过拟合。
对于一个 m × n m \times n m×n的矩阵 A A A,它的 L1 范数定义为:
∣ A ∣ 1 = max 1 ≤ j ≤ n ∑ i = 1 m ∣ a i j ∣ |A|_1 = \max_{1\leq j\leq n} \sum_{i=1}^{m} |a_{ij}| ∣A∣1=1≤j≤nmaxi=1∑m∣aij∣
其中, j j j表示矩阵 A A A的第 j j j列, ∑ i = 1 m ∣ a i j ∣ \sum_{i=1}^{m} |a_{ij}| ∑i=1m∣aij∣表示第 j j j 列中各个元素的绝对值之和。换句话说,L1 范数是将每一列的绝对值相加,然后取其中的最大值。
PyTorch 中其对应的参数为ord='1',例如:
A = torch.tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],dtype=torch.float)
norm_1 = np.linalg.norm(A, ord=1)
print(norm_1)
# 输出 18,即 max{1+4+7, 2+5+8, 3+6+9}
同理ord=-1表示取最小值。
L2范数
L2范数(L2 norm)也称为谱范数(spectral norm),或者最大奇异值范数(maximum singular value norm),是矩阵范数中的一种。
L2范数可以被用于衡量向量的大小,也可以被用于衡量向量之间的距离,具有一些特殊的性质,例如在最小化误差的时候,L2范数可以找到唯一的最小化点,而L1范数可能有多个最小化点。
对于一个 m × n m \times n m×n 的矩阵 A A A,它的L2范数定义为:
∣
A
∣
2
=
σ
max
(
A
)
|A|_2 = \sigma_{\max}(A)
∣A∣2=σmax(A)
其中,
∣
⋅
∣
2
|\cdot|_2
∣⋅∣2 表示向量的 L2 范数,
σ
max
(
A
)
\sigma{\max}(A)
σmax(A) 表示矩阵
A
A
A 的最大奇异值(singular value)。
在实际应用中,计算矩阵的 L2 范数可以使用 SVD 分解,例如:
PyTorch 中其对应的参数为ord='2',例如:
A = torch.tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype=torch.float)
norm_2 = torch.linalg.norm(A, ord=2)
u, s, v = torch.svd(A)
print(s)
print(norm_2)
# 输出 16.84810352325432
同理ord=-2表示取最小奇异值。
原创不易,请勿转载(
本不富裕的访问量雪上加霜)
博主首页:https://wzlodq.blog.csdn.net/
来都来了,不评论两句吗👀
如果文章对你有帮助,记得一键三连❤