拓扑排序

首先要说明一点：拓扑排序是针对图这种数据结构的特有排序。

百度百科对拓扑排序是这样定义的：

上面的解释不是特别好懂，学过离散数学才知道偏序和全序的概念，这里我就给个通俗一点的理解：访问图的顶点时，保证每次访问的顶点前面没有别的顶点(入度为0)，即访问的顶点只作为弧的弧头。

例如：

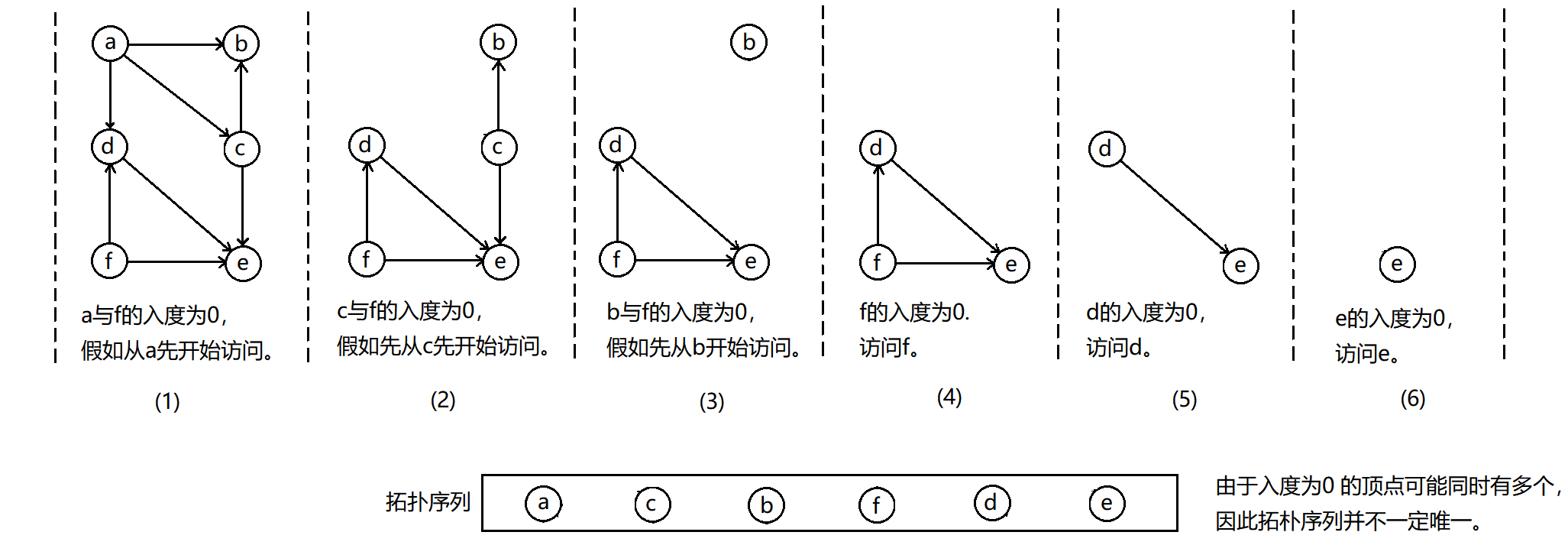
满足拓扑排序的前提：图中没有环

如果出现了环，那么就会出现一种情况：在环中一直寻找入度为0的顶点，只有找到了，才能打破没有顶点入度为0的循环，但现在缺的就是环中入度为0的一个顶点。这就造成了死循环。如下：

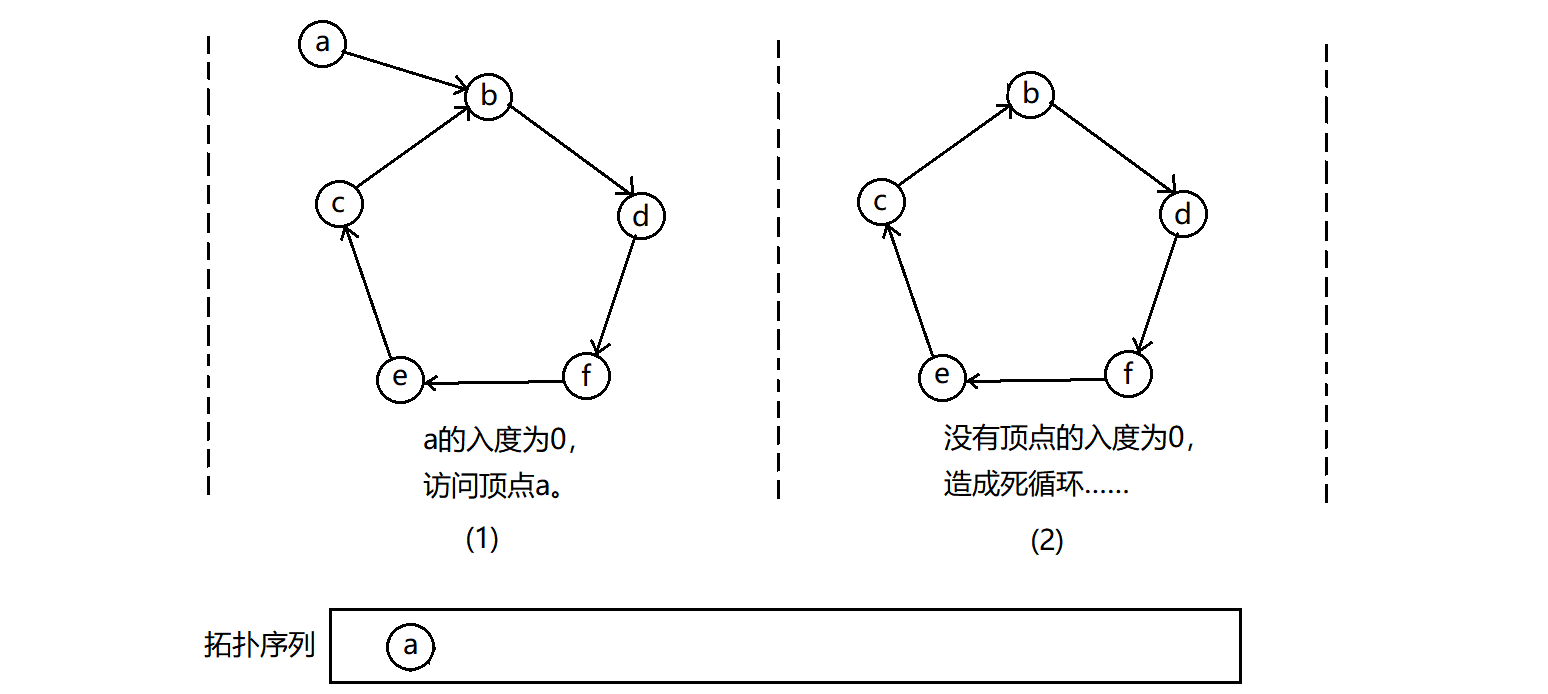
无论是从哪个路径入环，都会造成死循环。

拓扑排序的实现

访问顶点之前得先知道各个顶点的入度才行，因此得先遍历邻接矩阵，累计每个顶点的入度。并在访问完一个顶点之后，更新访问顶点的邻接点入度，也就是各自的入度自减1。这样循环检查，循环访问，直到所有的顶点被访问完就OK了。下面是用邻接矩阵来存储图的拓扑排序的代码实现。如果不是特别懂的话可以去看看我之前的博客（传送门），里面有详细讲解图的基本构造。

下面是图的一些基本构造和功能：

#include <iostream>
#include <vector>
#include <map>
#include <string>
#include <cstring>
using namespace std;
      顶点的数据类型 权值类型 权值的最大值默认为INT32_MAX，即∞    默认为无向图
template <class V, class W, W MAX_W = INT32_MAX, bool Direction = false>
class Graph//图的类框架
{
public:
    typedef Graph<V, W, MAX_W, Direction> Self;
    Graph() = default;
    Graph(const V *vertexs, int n)//顶点数组与个数传参
    {
        _vertexs.reserve(n);//初始化顶点数组与下标集
        for (int i = 0; i < n; ++i)
        {
            _vertexs.push_back(vertexs[i]);
            _indexMap[vertexs[i]] = i;
        }
        _matrix.resize(n);
        for (int i = 0; i < n; ++i)
        {
            _matrix[i].resize(n, MAX_W);//初始化邻接矩阵，每个元素默认赋值为∞
            _matrix[i][i]=W();//对角线上的权值为0
        }
    }
    size_t GetVertexIndex(const V& x)//获得顶点在顶点数组中的下标
    {
        auto it = _indexMap.find(x);
        if (it != _indexMap.end())//找到的话返回下标
        {
            return it->second;
        }
        else
        {
            throw invalid_argument("顶点不存在");//找不到的话就抛异常
            return -1;
        }
    }
    //添加关系(边)
    void _AddEdge(const size_t srci, const size_t dsti, const W& wight)
    {
        _matrix[srci][dsti] = wight;//两个顶点之间的权值进行赋值
        if (Direction == false)     //是无向图的话就在矩阵的对应位置也对边的权值进行赋值
        {
            _matrix[dsti][srci] = wight;
        }
    }
    //       参数：  起始顶点     终端顶点          权值
    void AddEdge(const V& src, const V& dst, const W& wight)
    {
        int srci = GetVertexIndex(src);//拿到起始顶点映射的下标
        int dsti = GetVertexIndex(dst);//拿到终端顶点映射的下标
        _AddEdge(srci, dsti, wight);   //嵌套一下用下标的方式添加边，方便在之后处理矩阵的特定情境通过下标加边。
    }
private:
    vector<V> _vertexs;        //顶点
    map<V, int> _indexMap;     //顶点对应的下标
    vector<vector<W>> _matrix; //矩阵
};

拓扑排序的代码：

//找所有顶点的入度
void FindInDegree(vector<int>& indegree) //indegree存的是所有顶点的入度
{
    size_t n = _vertexs.size(); //n为顶点的个数
    indegree.resize(n, 0); //入度初始化为0
    for (size_t i = 0; i < n; ++i) //对n个顶点进行各自的入度累计
    {
        for (size_t j = 0; j < n; ++j)
        {
            if (_matrix[i][j] != MAX_W && _matrix[i][j] != W())//有顶点i指向顶点j，顶点j的入度就自加1。
            {
                indegree[j]++;
            }
        }
    }
}
//拓扑排序         输出型参数 拓扑序列放在topo中
void TopologicalSort(vector<int>& topo)
{
    size_t n = _vertexs.size();//n为顶点的个数
    topo.resize(n, 0); //给topo开辟n个空间
    int index = 0;     //拓扑序列的实时下标，初始为0
    stack<int> st;        //存放入度为零的顶点
    vector<int> indegree; //所有顶点的初始入度
    vector<bool> visited(n, false); //标记映射的顶点是否被访问过
    FindInDegree(indegree);//查找所有顶点的入度
    for (size_t i = 0; i < n; ++i) // n个节点n次循环
    {
        for (size_t j = 0; j < n; ++j) //找未被访问且入度为零的顶点，将本次循环所有入度为0的顶点入栈
        {
            if (visited[j] == false && indegree[j] == 0)
            {
                st.push(j);
                visited[j] = true;//只要进栈，就意味着一定会被访问，直接先标记为已访问，避免重复检查
            }
        }
        int v = st.top();//取栈顶的入度为0的顶点下标
        topo[index] = v;//将该顶点下标存在拓扑序列中
        st.pop();//将该顶点出栈
        for (size_t j = 0; j < n; ++j)//已访问的顶点的所有未被访问的
        {
            if (visited[j] == false && _matrix[v][j] != MAX_W && _matrix[v][j] != W())
            {
                indegree[j]--; //更新已访问的顶点的邻接点的入度
            }
        }
        index++;//更新拓扑序列的实时下标
    }
}

拓扑排序测试

void TestTopologicalSort()
{
    vector<int> topo;
    const char* str="abcdef";
    Graph<char,int,INT32_MAX,true> g(str,strlen(str));
    g.AddEdge('a','b',1);
    g.AddEdge('a','d',1);
    g.AddEdge('a','c',1);
    g.AddEdge('d','e',1);
    g.AddEdge('f','d',1);
    g.AddEdge('f','e',1);
    g.AddEdge('c','b',1);
    g.AddEdge('c','e',1);
    g.TopologicalSort(topo);
    for(size_t i=0;i<topo.size();++i)
    {
        cout<<str[topo[i]]<<"["<<topo[i]<<"] ";
    }
    cout<<endl;
}

💻测试结果：

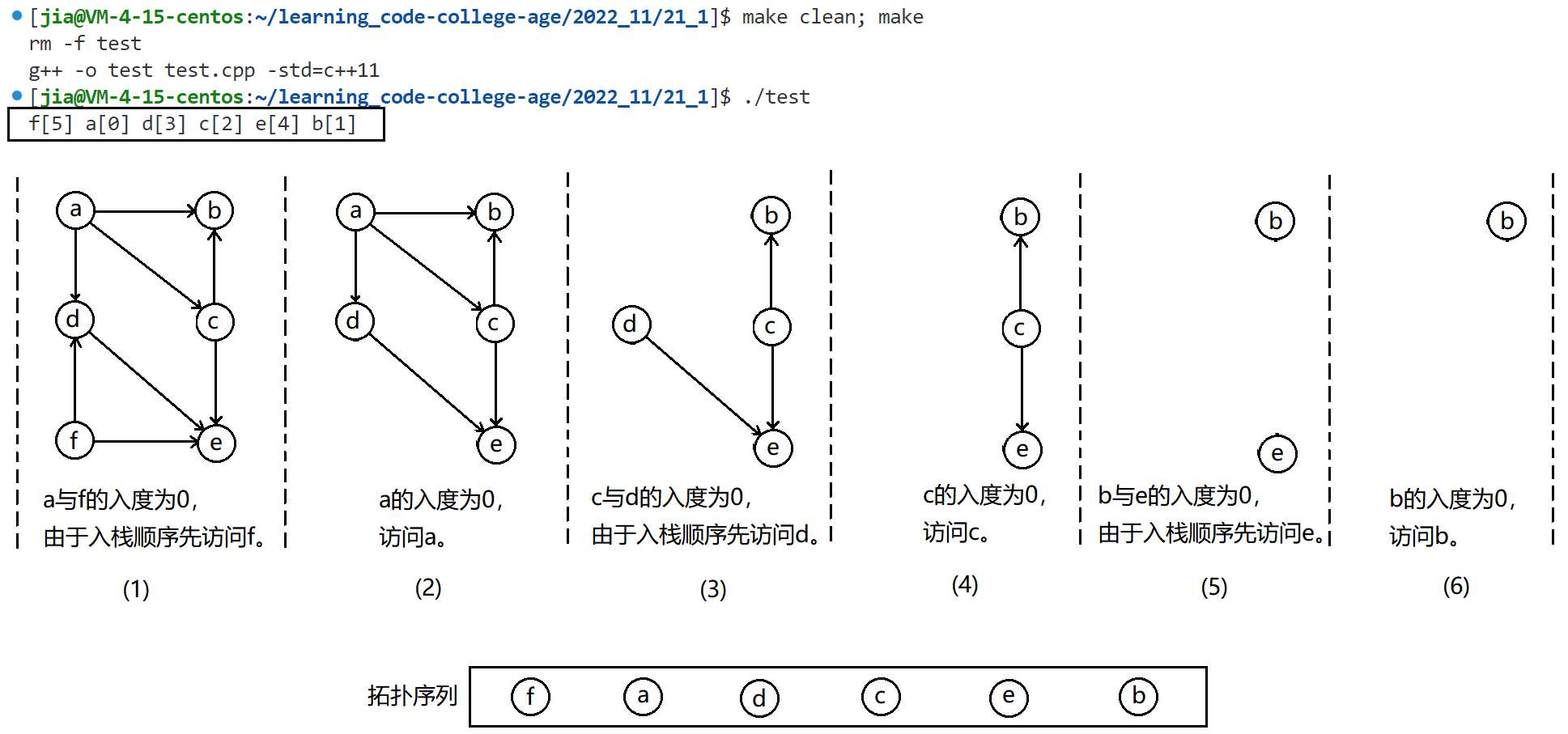
图一摸一样，但是却和最开始我们得到的拓扑序列有所差别，这正好验证了拓扑序列在有些情况下并不唯一的情况。所以结果是没有错的，这是由于栈的先进后出特性导致的。