栈的简单实现及其应用
- 什么是栈?
- 栈的分类
- 栈的数据结构
- 栈的基本操作
- 栈的初始化
- 栈的销毁
- 入栈操作
- 出栈和栈空的判断
- 获取栈顶元素
- 获取栈的元素个数
- 头文件
- 总结
- 栈的应用
什么是栈?
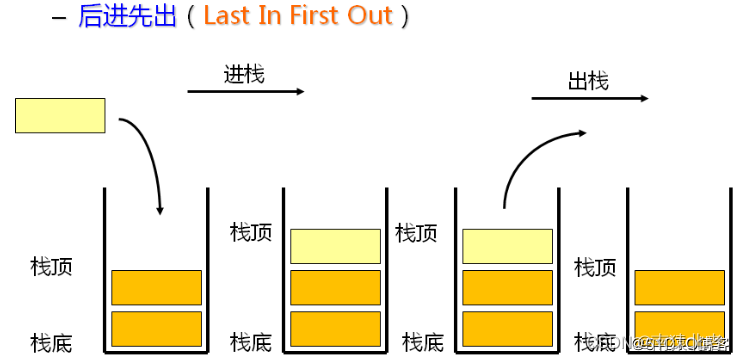
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
入栈:栈的插入操作叫做进栈/压栈/入栈;(从栈顶插入数据)
出栈:栈的删除操作叫做出栈;(也是从栈顶删除数据)
做个简单的比喻:我们的栈就相当于一个弹夹,入栈操作就相当向弹夹之中压入子弹;出栈操作就相当将弹夹里面的子弹取出来;而这个压入子弹和取出子弹都只有一个口;这个口就是栈顶,出入数据都从栈顶进行;
压栈和出栈:
栈的分类
栈主要分为两类:
1、顺序栈;(用顺序表实现的栈)
2、链式栈;(用链表实现的栈)
日常情况下,我们通常会选用顺序表来实现栈?
为什么?
因为如果我们将顺序表的尾作为栈顶的话,入栈(尾插)、出栈(尾删)效率很高就是O(1);
当然理论上我们也可以将顺序表的头作为栈顶,但是没人会这样高,因为入栈(头插)、出栈(头删)效率很低,时间复杂度是O(N^2)是一种事倍功半的操作;
那既然这样的话,我们为什么不选单链表的头做为栈顶,这样的话入栈(头插)、出栈(头删)效率也很高啊,时间复杂度也是O(1);
那么为什么不选它嘞?
我们目前来看是这样,但是具体实现起来,我们就得用一个栈顶指针来维护这个栈,那么就需要考虑很多特俗情况,同时参数这块也需要传二级指针,因为我的栈顶指针(链表头节点指针)是会变的;
而如果利用顺序表实现的话,就不会存在传二级指针的问题,也不需要考虑过多的特殊情况;
为此我们强烈推荐利用顺序表来实现栈!!!
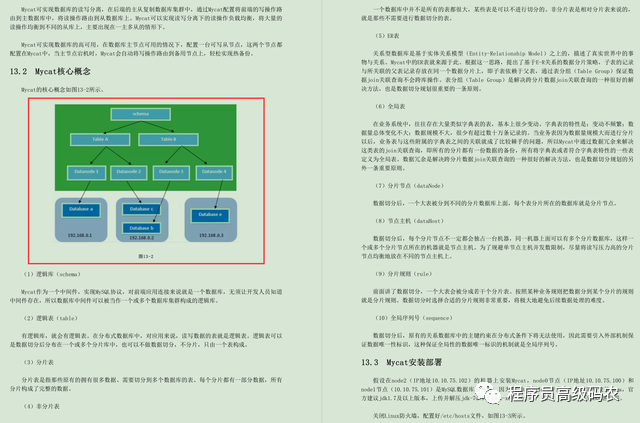
栈的数据结构
为了维护这一个栈,我们利用一个结构体来维护栈;
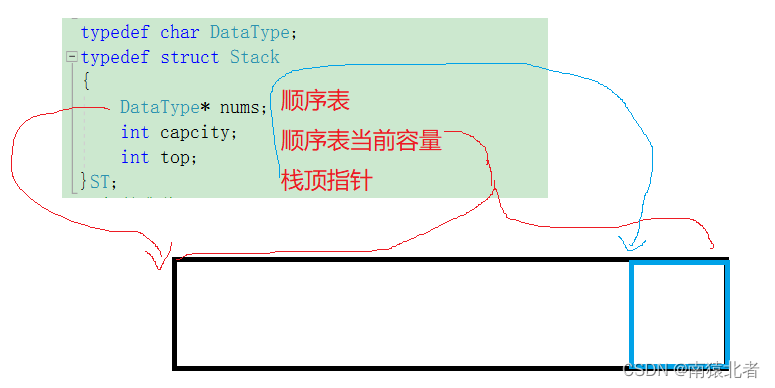
这里我们只需与顺序表区分一下top指针,top指针是专门用来维护栈顶元素的;
栈的基本操作
栈的初始化
刚开是一定是空栈,这点毋庸置疑;
所以我们结构体里面的nums置空,容量capcity也应该置空;
但是这里的top指针有两种初始化方式:
1、top=-1;
2、top=0;
这两种初始化方式对应着后面的操作有些不同;
如果top初始化为-1,那么我的栈顶元素是那个?
是不是就是nums[top],我的top每次都是指向上一次的空间的,为此我们每一次入栈,都要先将top++,在将数据放入top所指位置;为此我的top指针就指向最后一个空间(栈顶位置);
如果我的top指针初始化为0的话,我就不需要先++top了,直接在top位置插入数据就可以了,因为此时top位置就是待插入数据的位置,为此我们数据插入完毕过后需要++top,而此时的top表示的是栈顶元素的下一个位置top-1才表示栈顶元素的位置,这时的top也就相当于顺序表里面元素个数也就相当于顺序表里面的size;
本文采用top=0;的初始化方式:
//初始化栈
void InitStack(ST* ps)
{
assert(ps);//防止乱传
ps->capcity = 0;
ps->top = 0;
ps->nums = NULL;
}
栈的销毁
销毁与初始化操作通常都是连载一起的,我们在初始化操作实现完成过后便可直接实现销毁操作:
//销毁栈
void DestroyStack(ST*ps)
{
assert(ps);
ps->capcity = 0;
ps->top = 0;
free(ps->nums);
}
入栈操作
入栈操作对于顺序表来说就是尾插,既然是要插入数据,我们就要首先检查一下容量够不够,不免容量不够而出现插入失败的情况:
检查容量:
//检查扩容,不提供给用户,由程序自己完成
static void Check_Capcity(ST* ps)
{
assert(ps);
if (ps->capcity == ps->top)//需要扩容
{
int len = (ps->capcity == 0) ? 4 : ps->capcity * 2;
DataType* tmp = (DataType*)realloc(ps->nums,len*sizeof(DataType));
if (!tmp)
{
printf("realloc fail!\n");
exit(EXIT_FAILURE);
}
ps->nums = tmp;
ps->capcity = len;
}
}
当然这个检查容量的操作是由程序自己完成的,我们使用者是用不到的,为此我们可以将这个函数加以static关键字加以修饰,以此切断它的外部链接属性,不把它暴露给用户,加强其封装性!!!
容量问题现在解决了,接下来便是插入数据(入栈):
//入栈
void StackPush(ST* ps,DataType x)
{
assert(ps);
Check_Capcity(ps);
ps->nums[ps->top] = x;
ps->top++;
}
出栈和栈空的判断
当然出栈的操作,必然伴随着数据的删除,为此我们必须保证有数据可删才行!!数据都没了,那还删个der!为此我们需要先实现一下栈的判空:
由于我么初始化的时候选择的是将top初始化为0,那么top的数据就是元素个数,为此top==0是便是栈为空,我们便返回真;栈不为空,便返回假:
//判断栈是否为NULL
bool StackEmpty(ST* ps)
{
assert(ps);
return !ps->top;
}
接下来我们保证了数据有的删,那我们直接移动top指针就行了,让计算机访问不到,不用真的删除并释放,同时free也不支持只释放不完整的空间;
//出栈
void StackPop(ST* ps)
{
assert(ps);
assert(!StackEmpty(ps));//判空
ps->top--;
}
获取栈顶元素
同理可得,我们获取元素,那也得要栈里面有元素才行,栈都为空,就没必要再去取元素了:
为此,我们首先要先判断一下栈是不是为NULL:
//获取栈顶元素
DataType StackTop(ST* ps)
{
assert(ps);
assert(!StackEmpty(ps));//栈不为空,我们才有元素获取;
return ps->nums[ps->top - 1];
}
获取栈的元素个数
我们初始化的时候top初始化的0,为此,我们top所表示的意义和元素个数等价,为此我们只需返回top即可:
//统计栈的元素
size_t StackSize(ST* ps)
{
assert(ps);
return ps->top;
}
头文件
#pragma once
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<assert.h>
typedef char DataType;
typedef struct Stack
{
DataType* nums;
int capcity;
int top;
}ST;
//初始化栈
void InitStack(ST* ps);
//销毁栈
void DestroyStack(ST* ps);
//入栈
void StackPush(ST* ps,DataType x);
//出栈
void StackPop(ST*ps);
//判断栈是否为NULL
bool StackEmpty(ST* ps);
//统计栈的元素
size_t StackSize(ST* ps);
//获取栈顶元素个数
DataType StackTop(ST*ps);
总结
或许有的读者会疑惑,我们为什么要单独对栈顶元素和栈的元素个数专门写个函数呢?我们直接一句printf不就搞定了嘛。比如:我直接printf(“%d\n”,st.top);不就是栈的元素嘛,为啥还要专门写个函数;
我们现在是知道top是初始化为0,然后top就直接就表示元素个数,那如果我初始化top为-1,那么此时我的top就不再等价表示顺序表元素个数了,top+1才是表示元素个数,这也就意味着我需要去查看源码到底是怎么初始化top的,很是麻烦,而且难免有时候看错😊😊😊,而我们直接使用函数接口去求栈的元素个数,则不需要关心top是怎么初始化的,直接调就行了,很是方便,也不会出错!!就问这两种方式你更青睐与哪一种,我比较喜欢第二种!!😊😊😊
栈的应用
上面介绍了什么是栈,同时也介绍了栈的基本操作,下面我们就来做上一道题,感受一下栈的威力!!
题目描述:
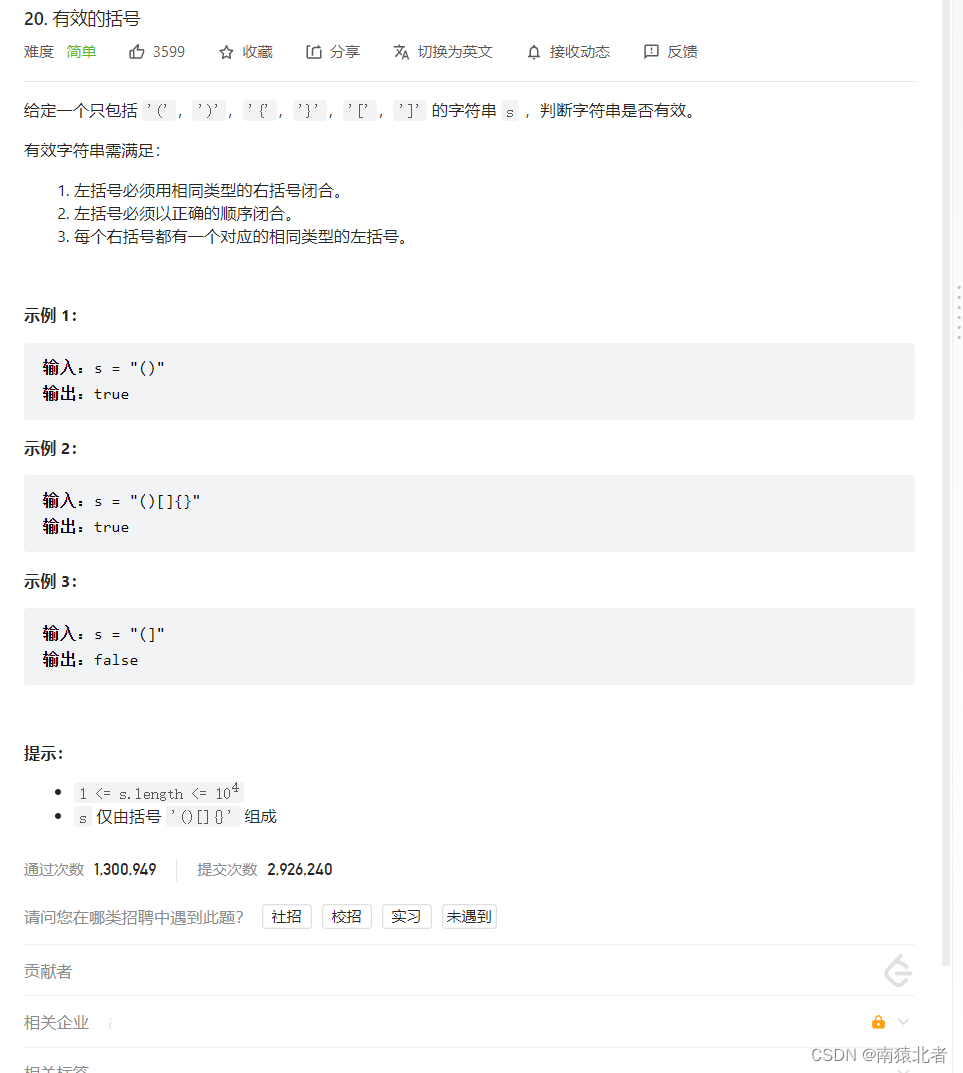
➡️挑战链接⬅️
分析:
思路:
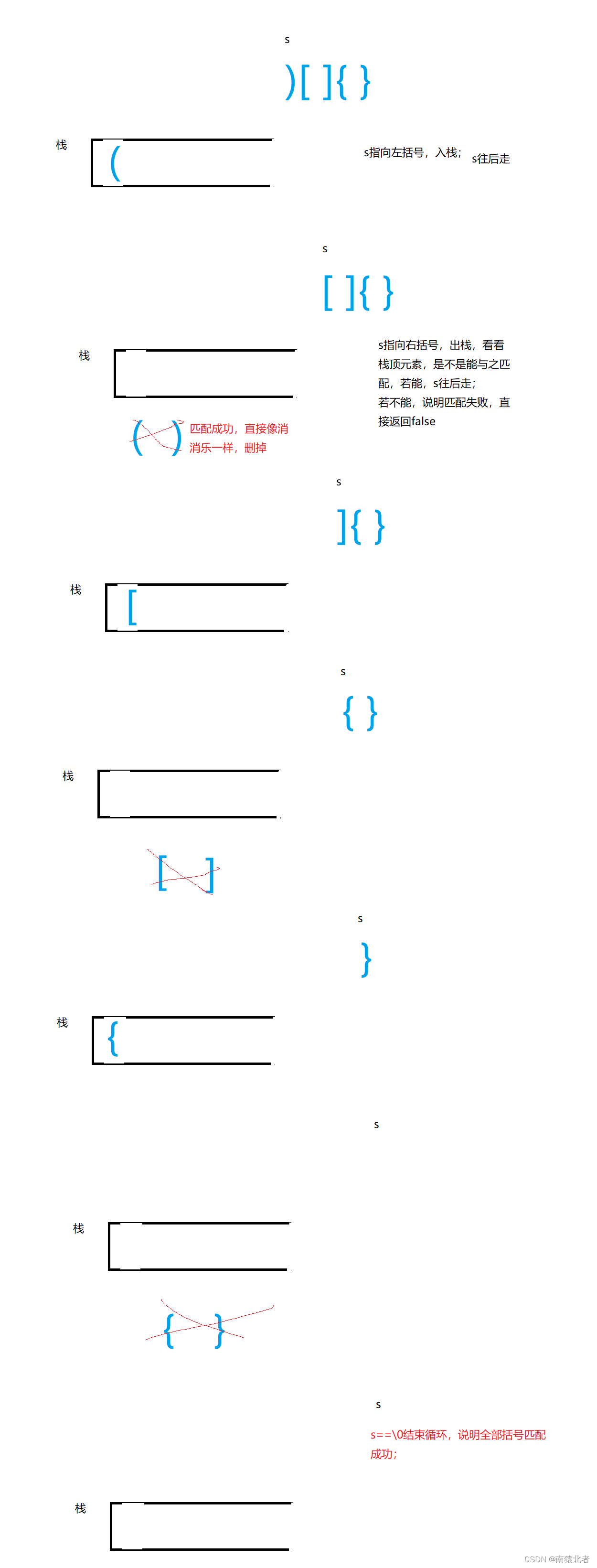
我们可以利用栈先进后出的特点:
遇到左括号就进栈,遇到右括号就获取栈顶元素,并且出栈;
举个例子:
为此我们来写我们的第一次代码:
由于C语言没有栈,所以我们需要将我们写的栈copy过去,才行:
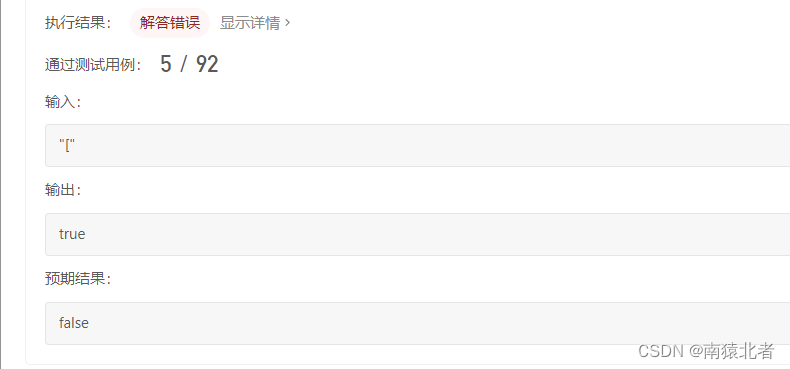
运行失败!!
通过测试用例,我们在走读代码,发现当只有左括号的时候,就会出现一直进栈,没有出栈的操作,自然也就不会走到false位置,最后直接就会来到treu位置,为此我们通过测试用例可以相当,如果全部能够匹配成功的话,那么我的栈最后一定是没有剩余元素的,如果有,那么说明一定还存在左括号没有匹配成功;为此我们的代码改进如下:
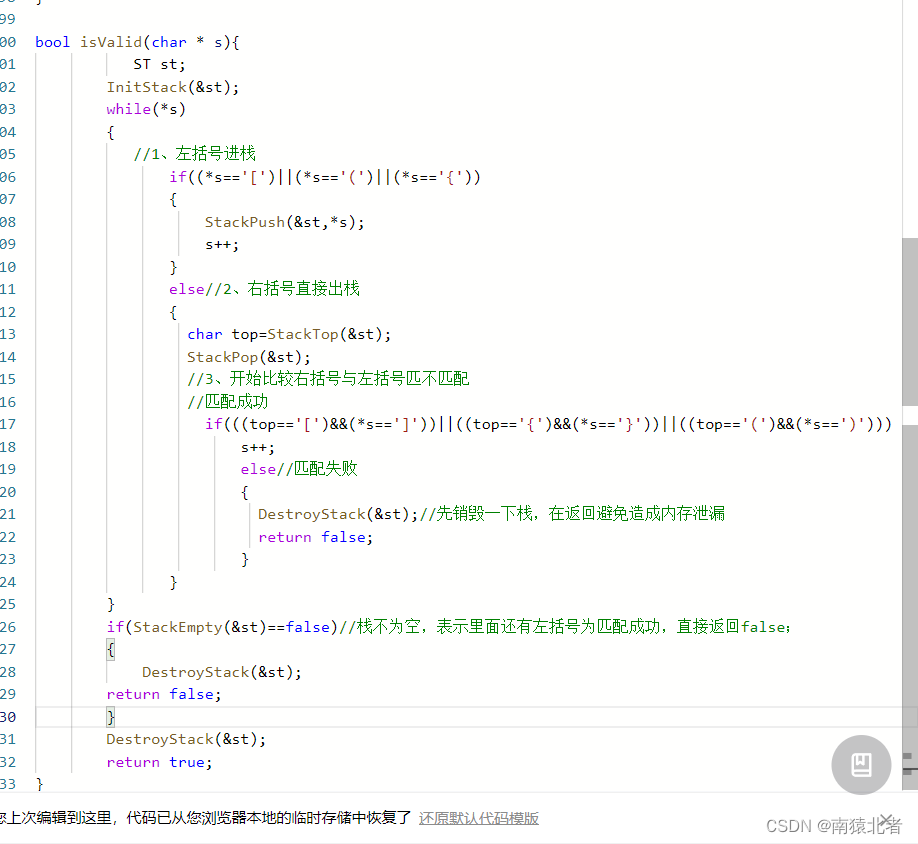
再次运行:
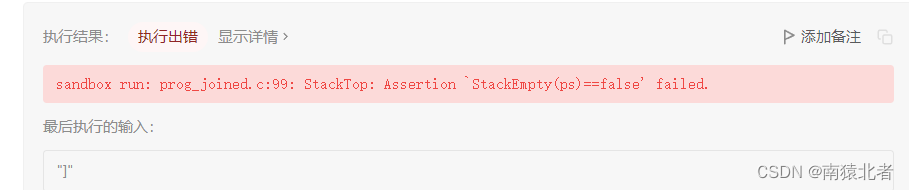
还是失败!!
这次他给我们报的测试用例是全是右括号的情况,假设全是右括号,按照上面的逻辑,我就需要去进行出栈操作,可是由于全是右括号,没有左括号给我们入栈,栈里面自然也就没有元素给我们出,这种情况就是我遇到了右括号,但是没有左括号与我匹配,我直接就返回false;
代码改进:

这次代码就过了:
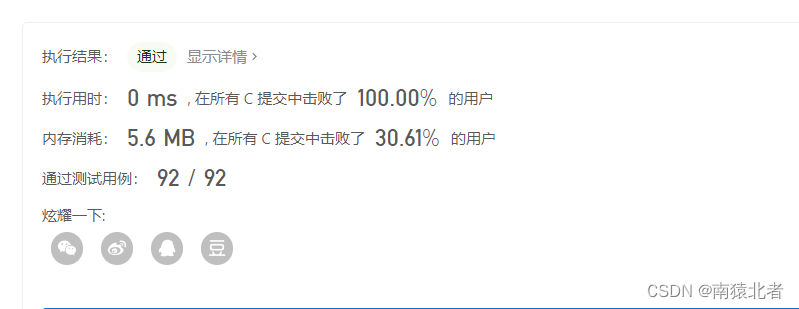
时间复杂度:O(N)
空间复杂度:O(N)
具体代码:
typedef char DataType;
struct ListNodes
{
DataType val;
struct ListNodes* next;
};
typedef struct Stack
{
int size;
struct ListNodes* Head;
}ST;
//初始化栈
void InitStack(ST*ps);
//销毁栈
void DestroyStack(ST* ps);
//入栈
void StackPush(ST*ps,DataType x);
//出栈
void StackPop(ST*ps);
//统计栈里元素个数
size_t StackSize(ST*ps);
//判断栈是否为NULL
bool StackEmpty(ST* ps);
//获取栈顶元素
DataType StackTop(ST* ps);
//初始化栈
void InitStack(ST* ps)
{
assert(ps);
ps->Head = NULL;
ps->size = 0;
}
//销毁栈
void DestroyStack(ST* ps)
{
assert(ps);
struct ListNodes* cur = ps->Head;
while (cur)
{
struct ListNodes* next = cur->next;
free(cur);
cur = next;
}
ps->Head = NULL;
ps->size = 0;
}
//创建节点,程序自动创建,用户无需关心
static struct ListNodes* BuyListNode(DataType x)
{
struct ListNodes* NewNode = (struct ListNodes*)malloc(sizeof(struct ListNodes));
if (NewNode == NULL)
{
printf("malloc fail!\n");
exit(EXIT_FAILURE);
}
NewNode->next = NULL;
NewNode->val = x;
return NewNode;
}
//入栈
void StackPush(ST* ps, DataType x)
{
assert(ps);
struct ListNodes* NewNode = BuyListNode(x);
struct ListNodes* next = ps->Head;
NewNode->next = next;
ps->Head = NewNode;
ps->size++;
}
//出栈
void StackPop(ST* ps)
{
assert(ps);
assert(!StackEmpty(ps));
struct ListNodes* next = ps->Head->next;
free(ps->Head);
ps->size--;
ps->Head = next;
}
//判断栈是否为NULL
bool StackEmpty(ST* ps)
{
assert(ps);
return ps->size == 0;
}
//统计栈里元素个数
size_t StackSize(ST* ps)
{
assert(ps);
return ps->size;
}
//获取栈顶元素
DataType StackTop(ST* ps)
{
assert(ps);
assert(StackEmpty(ps)==false);
return ps->Head->val;
}
bool isValid(char* s) {
ST st;
InitStack(&st);
while (*s)
{
//1、左括号进栈
if ((*s == '[') || (*s == '(') || (*s == '{'))
{
StackPush(&st, *s);
s++;
}
else//2、右括号直接出栈
{
if (StackEmpty(&st))//表示栈里还没有元素,但是我的s指向右括号,无法与我的右括号匹配
{
DestroyStack(&st);
return false;
}
char top = StackTop(&st);
StackPop(&st);
//3、开始比较右括号与左括号匹不匹配
//匹配成功
if (((top == '[') && (*s == ']')) || ((top == '{') && (*s == '}')) || ((top == '(') && (*s == ')')))
s++;
else//匹配失败
{
printf("top==%c s==%c\n", top, *s);
DestroyStack(&st);//先销毁一下栈,在返回避免造成内存泄漏
return false;
}
}
}
if (StackEmpty(&st) == false)//栈不为空,表示里面还有左括号为匹配成功,直接返回false;
{
DestroyStack(&st);
return false;
}
DestroyStack(&st);
return true;
}