目录
一.引言
二.决策树基础-信息熵
三.决策树的算法基础 - ID3 算法
四.ML 中决策树的构建
1.信息增益计算
2.连续属性划分
五.ML 决策树实战
1.Libsvm 数据与加载
2.StringIndexer
3.VectorIndexer
4.构建决策树与 Pipeline
5.测试与评估
6.获取决策树
六.总结
一.引言
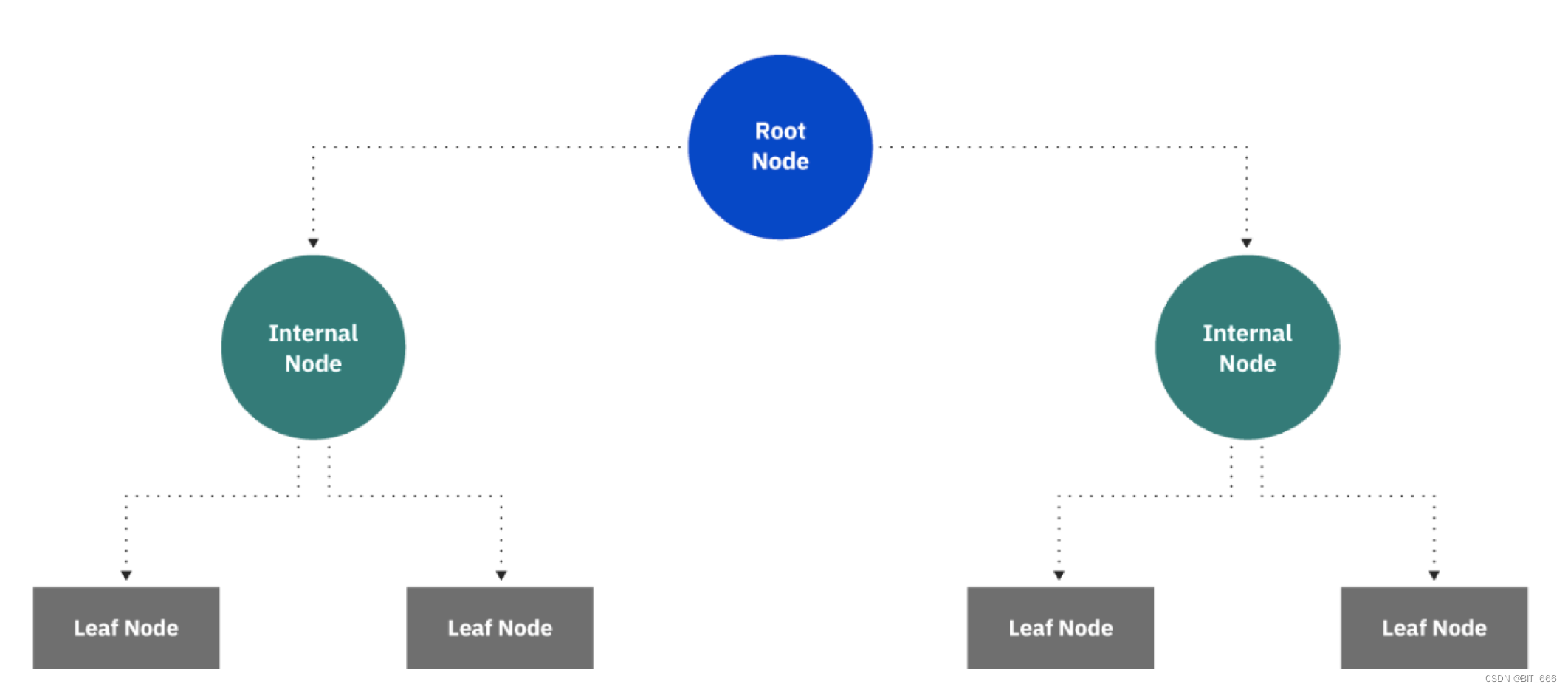
决策树是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评估项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于其决策分支画成图像很像一颗树的枝干,故称之为决策树。
二.决策树基础-信息熵
信息熵指的是对事件中不确定的信息度量。一个事件或属性中,其信息熵越大代表其不确定因素越大,对数据分析的计算更有益。因为熵其实用来描述一个物体或事件内部的混乱程度。在一个事件中,需要计算各个属性的不同信息熵。如果事件中包含 n 个属性,且个属性事件彼此独立、无相关性,此时可以将信息熵定义为单个属性的对数平均值:
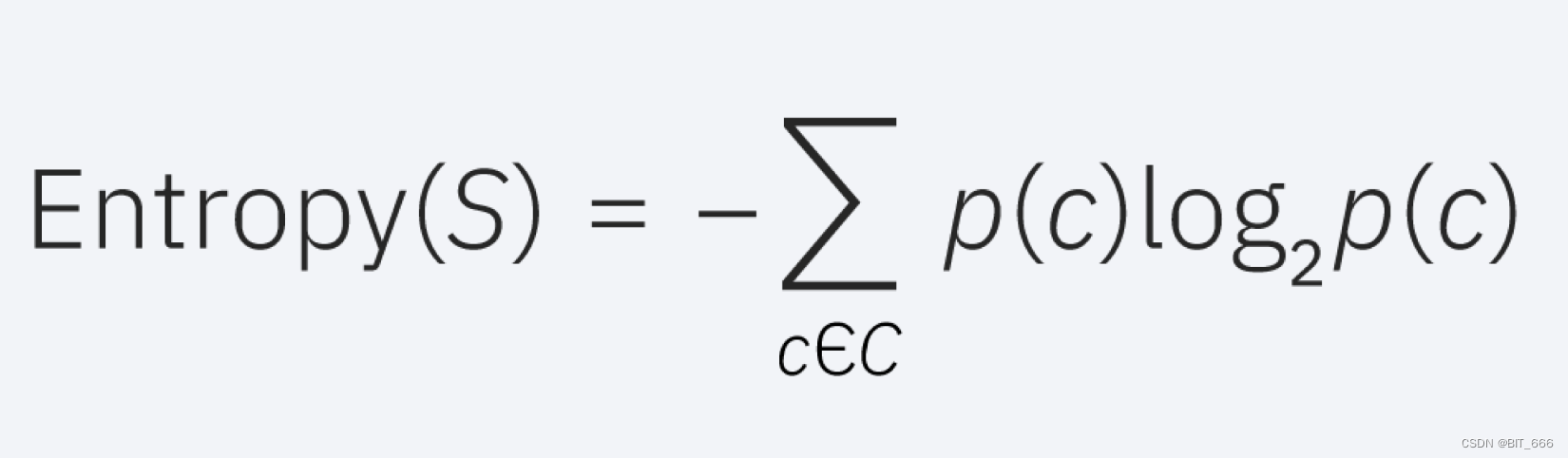
举个栗子 🌰:
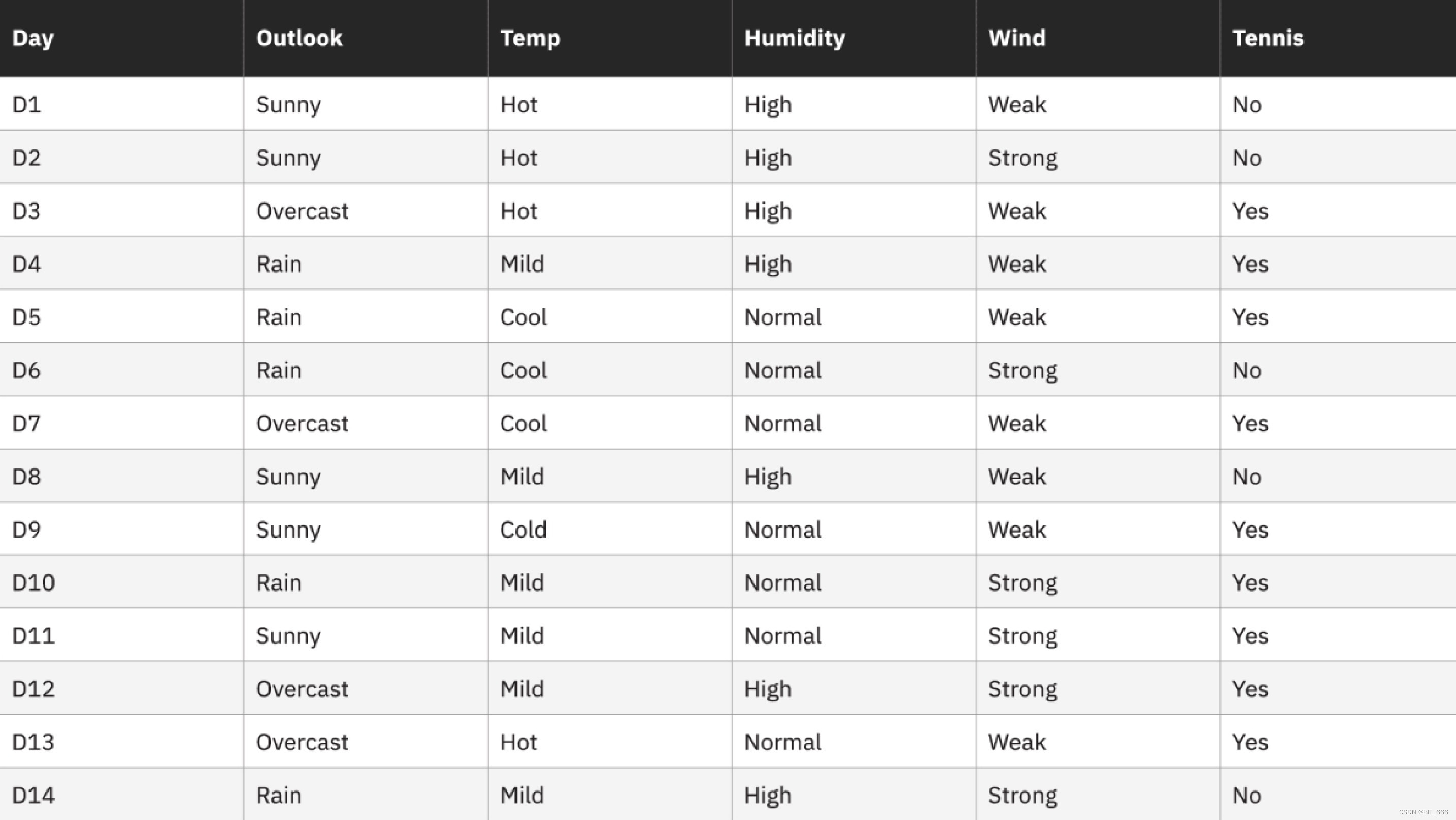
上述描述了 14 天中不同的天气属性以及是否出门打网球:
即是否出门打网球这个属性的信息熵 Entropy 为 0.918,同理以 Humidity 湿度为属性计算 Tennis 的信息熵:
其中 High 情况下 Tennis Yes 3 次,No 4 次,Normal 情况下 Tennis Yes 6 次,No 1 次:

通过计算对数平均值可以获得条件概率下不同属性的信息熵。使用下述方法可以轻松计算一个属性的信息熵:
def calcEntropy(pArr: Array[Double]): Double = {
var sum = 0D
pArr.foreach(p => {
sum += -1.0 * p * log2(p)
})
sum
}
def log2(p: Double): Double = {
Math.log(p) / Math.log(2) // Math.log的底为e
}三.决策树的算法基础 - ID3 算法
上面介绍了信息熵,下面基于这个概念介绍如何尽可能的建立一颗最短的、最小的且最有效的决策树。ID3 算法是基于信息熵的一种经典决策树构建方法,其以信息熵的下降速度为选取测试属性的标准,即在每个节点选取还尚未用来划分的、具有最高信息增益的属性作为划分标准并不断重复这个过程,直到生成的决策树可以完美分类训练样例。其核心为信息增益:
信息增益,指的是一个时间前后发生的不同信息之间的差值,即在决策树生成过程前后不同的信息熵差值,公式可以表达为:
以上面的 Tessins 与 Humidity 为例:
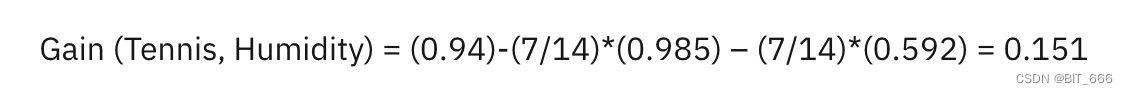
然后,重复上表中每个属性的信息增益计算,并选择信息增益最高的属性作为决策树中的第一个分割点。在这种情况下,outlook 产生了最高的信息增益。然后,对每个子树重复该过程。
四.ML 中决策树的构建
1.信息增益计算
Spark ML 实现了支持使用连续和离散特征的二元和多类分类以及回归的决策树。该实现按行对数据进行分区,允许使用数百万甚至数十亿个实例进行分布式训练。决策树构建采用递归二分法方式。不断从根节点进行生成,直到决策树的需求信息增益满足一定条件为止:
Left、right 为待计算属性,每增加一个分类节点,待计算属性便减少一个。
2.连续属性划分
上面介绍的 Tennis,其属性均为离散属性,实际应用中会有大量的连续性特征,解决办法就是在计算时根据需要将数据划分为若干个部分进行处理。这些被划分的若干部分在 ML 中称为 bin,即分箱的意思。每个作为分割点的节点被称为 split。决策树是一种贪婪算法,其通过从每一组可能的分割中选择最佳分割来贪婪的选择每个分割。例如一个连续特征为 {1,2,3,4,5},实际中采用二分法,此时 split 为3,划分得到 {1,2,3},{4,5} 两个 bin。
五.ML 决策树实战
1.Libsvm 数据与加载
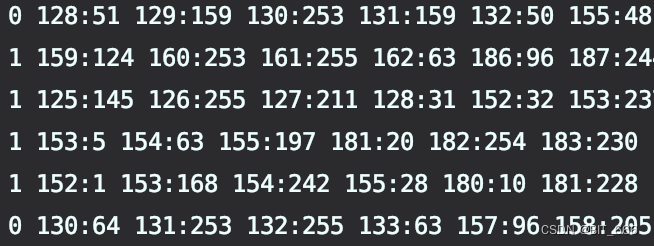
实战前首先熟悉一种数据格式-Libsvm:
数据的第一列为标签,以上面 Tennis 为例,1 代表出去,0 代表不出去,后面的 key 代表属性的序号,value 代表该属性的具体值。下面读取实战的数据:
val spark = SparkSession
.builder //创建spark会话
.master("local") //设置本地模式
.appName("DecisionTreeClassificationExample") //设置名称
.getOrCreate() //创建会话变量
spark.sparkContext.setLogLevel("error")
// 读取文件,装载数据到spark dataframe 格式中
val data = spark.read.format("libsvm").load("./sample_libsvm_data.txt")
通过 .format 指定 livsvm 格式即可读取对应格式文件,解析后获得一个两列的 DataFrame,一列为 label,另一列为 features。
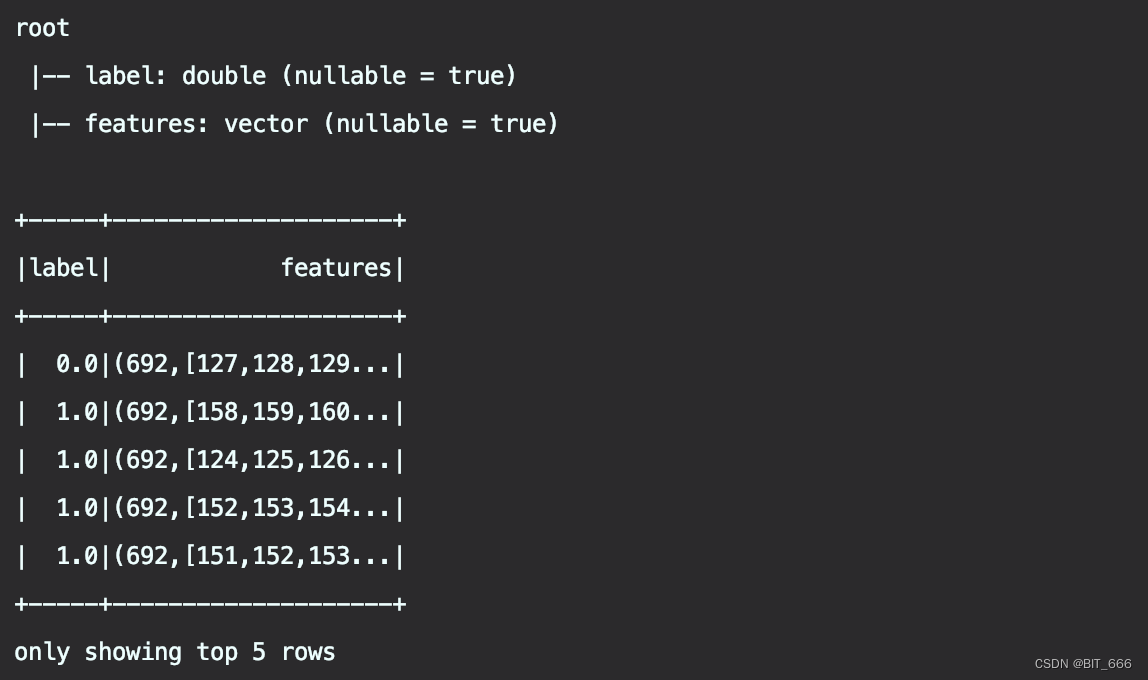
Tips:
细心的同学可能会发现,原始的数据为 128:x、129:y、130:z,为什么 features 里变成了 127、128、129 所有的索引的减了1,这是因为 Libsvm 数据格式从 1 开始,而我们的 features 的 Vector 内索引从 0 开始,所以需要将 libsvm 数据中的 key 都减去1,而 value 则不动。
2.StringIndexer
val labelIndexer = new StringIndexer()
.setInputCol("label")
.setOutputCol("indexedLabel")
.fit(data)字符索引器,通过遍历标签添加元数据到标签列,实现【标签 -> 序号】的映射,如果是数值型 Label,会先将 Label 转化为字符串,然后再进行索引化,如果 label 已经是字符串,则直接进行索引化。其中标签索引的顺序按照标签出现的频率来排序,出现最多的 Label 索引即为0,依次逆序排列。
上面说的可能比较绕,简单解释下该函数的意义就是将不规则的 label 处理为有序的数字序号,例如原始标签有 A、C、E 三种类型,通过 StringIndexer 会变成 0、1、2,而对应的映射关系取决于 A、C、E 的出现次数,次数最多的索引为 0。E 出现最多,所以 E 的索引为0,以此类推。
+---+--------+-------------+
| id|category|categoryIndex|
+---+--------+-------------+
| 0| A| 1.0|
| 1| C| 2.0|
| 2| E| 0.0|
| 3| E| 0.0|
| 4| A| 1.0|
| 5| E| 0.0|
+---+--------+-------------+上面的实战数据我们转换看一下:

看到 label 0.0 变为 1.0, 1.0 变为 0.0,我们再用 Spark Sql 看下标签数据的分布:
val labelIndexDF = labelIndexer.transform(data)
labelIndexDF.show(5)
labelIndexDF.createOrReplaceTempView("LabelIndex")
spark.sql("select label,count(*) from LabelIndex group by label").collect().foreach(println)没毛病,label=1.0 的标签多,所以 1.0 被映射为 0.0。
[0.0,43]
[1.0,57]3.VectorIndexer
// 自动识别分类特征,并对其进行索引
val featureIndexer = new VectorIndexer()
.setInputCol("features") // 设置输入输出参数
.setOutputCol("indexedFeatures")
.setMaxCategories(5) // 具有多于5个不同值的特性被视为连续特征
.fit(data)该方法主要用于自动识别离散与分类特征,提高决策树 ML 方法的分类效果。其中 MaxCategories 参数设置一个数值,如果某个特征的取值类型多于该参数,则该参数会被认定为连续特征,不作处理,反之会被认定为离散特征,并被重新编号为 0-K (K < MaxCategories)。
+-------------------------+-------------------------+
|features |indexedFeatures |
+-------------------------+-------------------------+
|(3,[0,1,2],[2.0,5.0,7.0])|(3,[0,1,2],[2.0,1.0,1.0])|
|(3,[0,1,2],[3.0,5.0,9.0])|(3,[0,1,2],[3.0,1.0,2.0])|
|(3,[0,1,2],[4.0,7.0,9.0])|(3,[0,1,2],[4.0,3.0,2.0])|
|(3,[0,1,2],[2.0,4.0,9.0])|(3,[0,1,2],[2.0,0.0,2.0])|
|(3,[0,1,2],[9.0,5.0,7.0])|(3,[0,1,2],[9.0,1.0,1.0])|
|(3,[0,1,2],[2.0,5.0,9.0])|(3,[0,1,2],[2.0,1.0,2.0])|
|(3,[0,1,2],[3.0,4.0,9.0])|(3,[0,1,2],[3.0,0.0,2.0])|
|(3,[0,1,2],[8.0,4.0,9.0])|(3,[0,1,2],[8.0,0.0,2.0])|
|(3,[0,1,2],[3.0,6.0,2.0])|(3,[0,1,2],[3.0,2.0,0.0])|
|(3,[0,1,2],[5.0,9.0,2.0])|(3,[0,1,2],[5.0,4.0,0.0])|
+-------------------------+-------------------------+上面示例中共有三个特征:
0 - [2,3,4,5,8,9] - 类别数为6,大于 MaxCategories,不执行划分
1 - [4,5,6,7,9],小于 MaxCategories,执行划分 [4,5,6,7,9] -> [0,1,2,3,4]
2 - [2,7,9],小于 MaxCategories,执行划分 [2,7,9] -> [0,1,2]
该方法主要用于离散特征与连续特征的区分,对于连续型特征,决策树的划分点划分多为 Feat >= threshold 的形式,而离散型的特征则多为 Feat in {value}。
4.构建决策树与 Pipeline
// 按照7:3的比例进行拆分数据,70%作为训练集,30%作为测试集。
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))
// 建立一个决策树分类器
val dt = new DecisionTreeClassifier()
.setLabelCol("indexedLabel")
.setFeaturesCol("indexedFeatures")
.setMaxDepth(2)
// 将索引标签转换回原始标签
val labelConverter = new IndexToString()
.setInputCol("prediction")
.setOutputCol("predictedLabel")
.setLabels(labelIndexer.labelsArray(0))
// 把索引和决策树链接(组合)到一个管道(工作流)之中
val pipeline = new Pipeline()
.setStages(Array(labelIndexer, featureIndexer, dt, labelConverter))
// 载入训练集数据正式训练模型
val model = pipeline.fit(trainingData)- DecisionTreeClassifier 主要属性有
Impuriry (String) : 计算信息增益的方式
maxDepth(Int) : 树的深度
maxBins(Int) : 能够分裂的数据集合数量
可以通过 dt.extractParamMap 方法获取当前模型的自定义参数与默认参数。
- IndexToString
该方法主要用于将转换后的 label 再映射回去,例如前面将 1->0 0->1 再重新反向映射回去:
// 按顺序来,相当于映射 0->1 1->0
println("=========Label Index=========")
println(labelIndexer.labelsArray(0).mkString(","))labelsArray 为如下形式,将其 zipWithIndex 再反转即可实现 label 的反向映射。
=========Label Index=========
1.0,0.0- pipeline
构建 Pipeline 之后即可实现 PipelineModel.fit 训练训练数据。
5.测试与评估
// 使用测试集作预测
val predictions = model.transform(testData)
// 选择一些样例进行显示
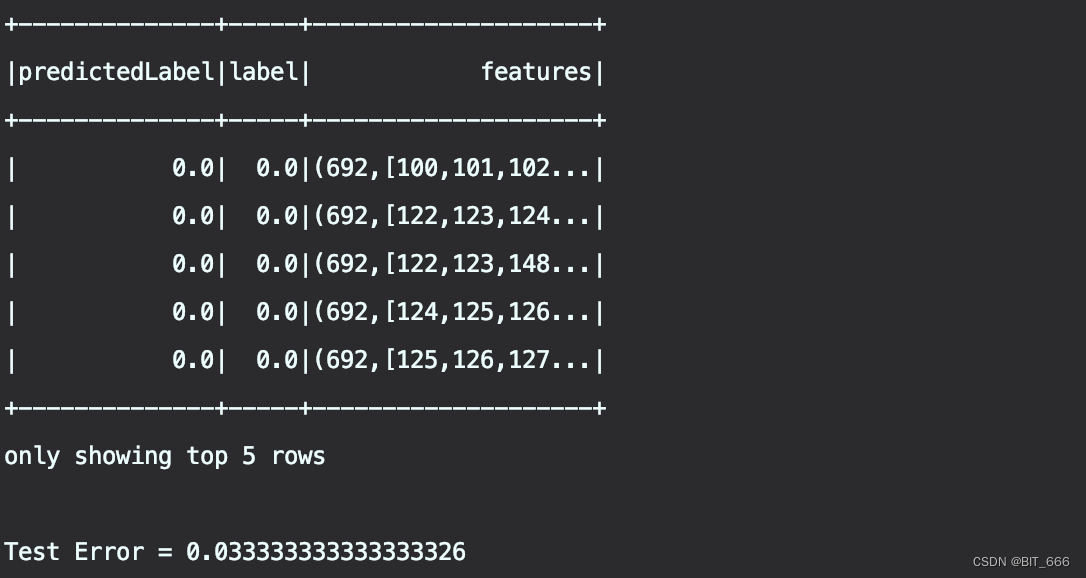
predictions.select("predictedLabel", "label", "features").show(5)
// 计算测试误差
val evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("indexedLabel")
.setPredictionCol("prediction")
.setMetricName("accuracy")
val accuracy = evaluator.evaluate(predictions)
println(s"Test Error = ${(1.0 - accuracy)}")使用 PipelineModel.transform 进行测试,使用 label 与 predict 进行 accuracy 的指标评估:
6.获取决策树
val treeModel = model.stages(2).asInstanceOf[DecisionTreeClassificationModel]
println(s"Learned classification tree model:\n ${treeModel.toDebugString}")使用 AsInstanceOf 将 Stage(2) 转化为 Dt 并调用 toDebugString 获取树的结构:
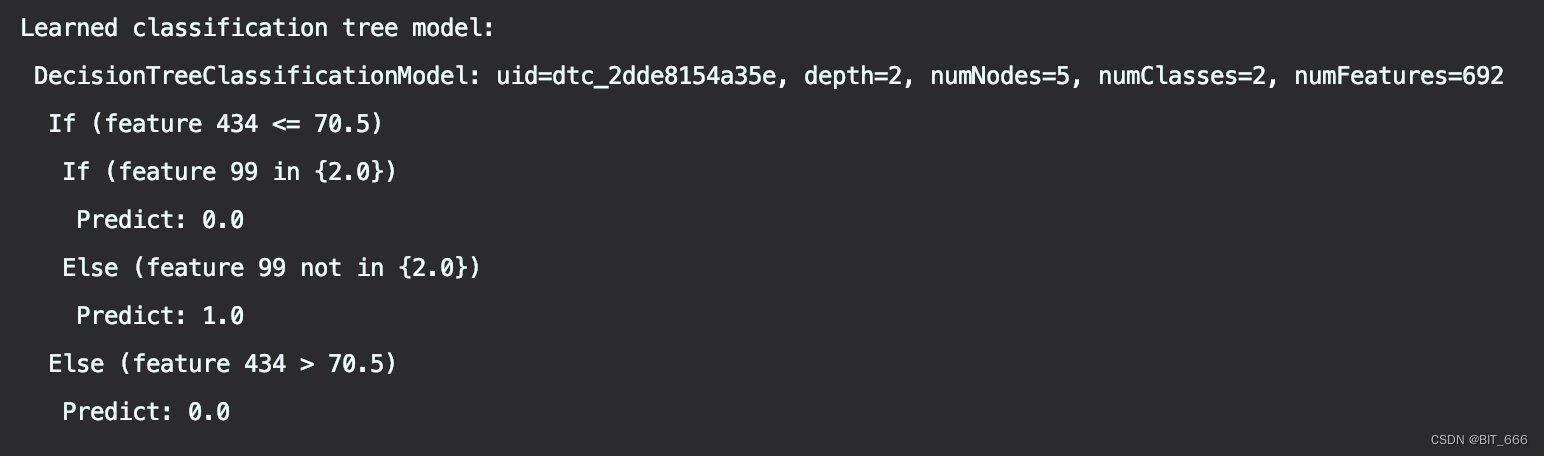
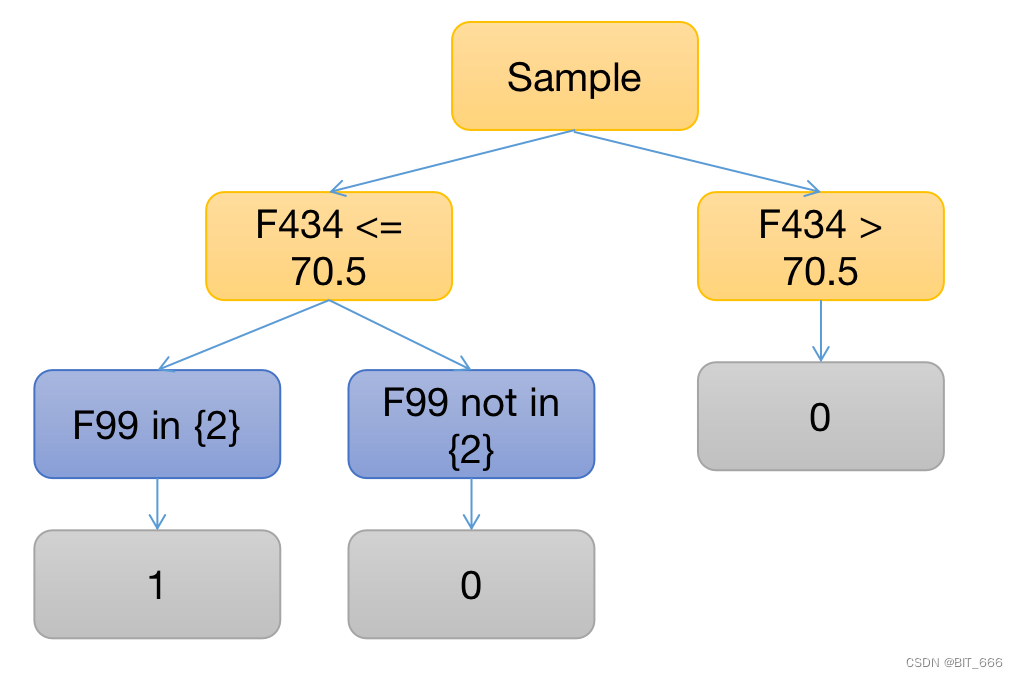
通过两层 If-Else 嵌套形式展示了一棵树,这样再来一个样本,我们可以轻易地判断其所属类别。
六.总结
本文根据样例数据进行了 Spark ML 决策树的 Demo 讲解,其中涉及到很多特征处理与转化的组件,可以通过样例进行熟悉,后续也会基于真实数据进行随机森林与梯度提升树的案例,加深对树的理解。




![[附源码]计算机毕业设计springboot环境保护宣传网站](https://img-blog.csdnimg.cn/d555f404e4ca4036975da00314b28766.png)