力扣杯2023春-个人赛

难度简单3

远征队即将开启未知的冒险之旅，不过在此之前，将对补给车队进行最后的检查。supplies[i] 表示编号为 i 的补给马车装载的物资数量。
考虑到车队过长容易被野兽偷袭，他们决定将车队的长度变为原来的一半（向下取整），计划为：

• 找出车队中 物资之和最小 两辆 相邻 马车，将它们车辆的物资整合为一辆。若存在多组物资之和相同的马车，则取编号最小的两辆马车进行整合；
• 重复上述操作直到车队长度符合要求。

请返回车队长度符合要求后，物资的分布情况。

示例 1：

输入：supplies = [7,3,6,1,8]

输出：[10,15]

解释：
第 1 次合并，符合条件的两辆马车为 6,1，合并后的车队为 [7,3,7,8]；
第 2 次合并，符合条件的两辆马车为 (7,3) 和 (3,7)，取编号最小的 (7,3)，合并后的车队为 [10,7,8]；
第 3 次合并，符合条件的两辆马车为 7,8，合并后的车队为 [10,15]；
返回 [10,15]

示例 2：

输入：supplies = [1,3,1,5]

输出：[5,5]

解释：

• 2 <= supplies.length <= 1000
• 1 <= supplies[i] <= 1000

System.arraycopy():一般用于数组的复制和数据替换，是System类中一个被关键词native修饰的方法。

public static native void arraycopy(
    Object src, // 数据源，被复制的对象
    int  srcPos, // 复制起始坐标
    Object dest,  // 目标对象
 	int destPos, // 目标对象开始复制的起始点
 	int length // 复制的数据长度
 );

难度中等2

探险家小扣的行动轨迹，都将保存在记录仪中。expeditions[i] 表示小扣第 i 次探险记录，用一个字符串数组表示。其中的每个「营地」由大小写字母组成，通过子串 -> 连接。

例：“Leet->code->Campsite”，表示到访了 “Leet”、“code”、“Campsite” 三个营地。

expeditions[0] 包含了初始小扣已知的所有营地；对于之后的第 i 次探险(即 expeditions[i] 且 i > 0)，如果记录中包含了之前均没出现的营地，则表示小扣 新发现 的营地。

请你找出小扣发现新营地最多且索引最小的那次探险，并返回对应的记录索引。如果所有探险记录都没有发现新的营地，返回 -1

注意：

• 大小写不同的营地视为不同的营地；
• 营地的名称长度均大于 0。

示例 1：

输入：expeditions = ["leet->code","leet->code->Campsite->Leet","leet->code->leet->courier"]

输出：1

解释：
初始已知的所有营地为 “leet” 和 “code”
第 1 次，到访了 “leet”、“code”、“Campsite”、“Leet”，新发现营地 2 处：“Campsite”、“Leet”
第 2 次，到访了 “leet”、“code”、“courier”，新发现营地 1 处：“courier”
第 1 次探险发现的新营地数量最多，因此返回 1

示例 2：

输入：expeditions = ["Alice->Dex","","Dex"]

输出：-1

解释：
初始已知的所有营地为 “Alice” 和 “Dex”
第 1 次，未到访任何营地；
第 2 次，到访了 “Dex”，未新发现营地；
因为两次探险均未发现新的营地，返回 -1

示例 3：

输入：expeditions = ["","Gryffindor->Slytherin->Gryffindor","Hogwarts->Hufflepuff->Ravenclaw"]

输出：2

解释：
初始未发现任何营地；
第 1 次，到访 “Gryffindor”、“Slytherin” 营地，其中重复到访 “Gryffindor” 两次，
因此新发现营地为 2 处：“Gryffindor”、“Slytherin”
第 2 次，到访 “Hogwarts”、“Hufflepuff”、“Ravenclaw” 营地；
新发现营地 3 处：“Hogwarts”、“Hufflepuff”、“Ravenclaw”；
第 2 次探险发现的新营地数量最多，因此返回 2

提示：

• 1 <= expeditions.length <= 1000
• 0 <= expeditions[i].length <= 1000
• 探险记录中只包含大小写字母和子串"->"

难度中等5

小扣在探索丛林的过程中，无意间发现了传说中“落寞的黄金之都”。而在这片建筑废墟的地带中，小扣使用探测仪监测到了存在某种带有「祝福」效果的力场。
经过不断的勘测记录，小扣将所有力场的分布都记录了下来。forceField[i] = [x,y,side] 表示第 i 片力场将覆盖以坐标 (x,y) 为中心，边长为 side 的正方形区域。

若任意一点的 力场强度 等于覆盖该点的力场数量，请求出在这片地带中 力场强度 最强处的 力场强度。

注意：

• 力场范围的边缘同样被力场覆盖。

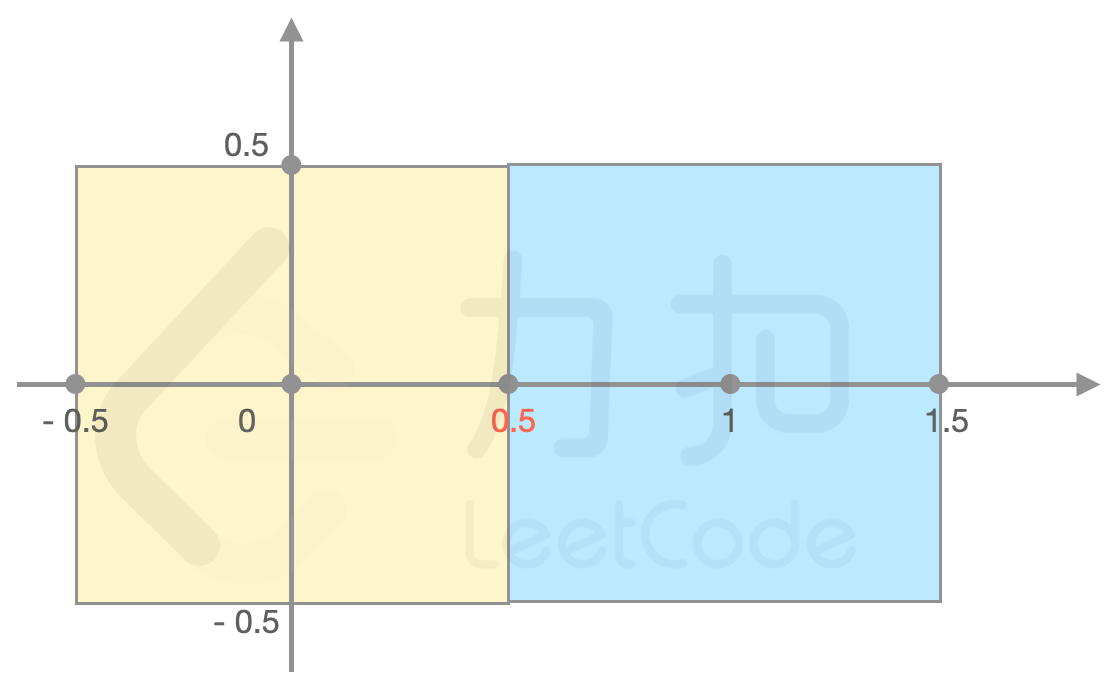
示例 1：

输入：
forceField = [[0,0,1],[1,0,1]]

输出：2

解释：如图所示，（0.5, 0) 处力场强度最强为 2， （0.5，-0.5）处力场强度同样是 2。

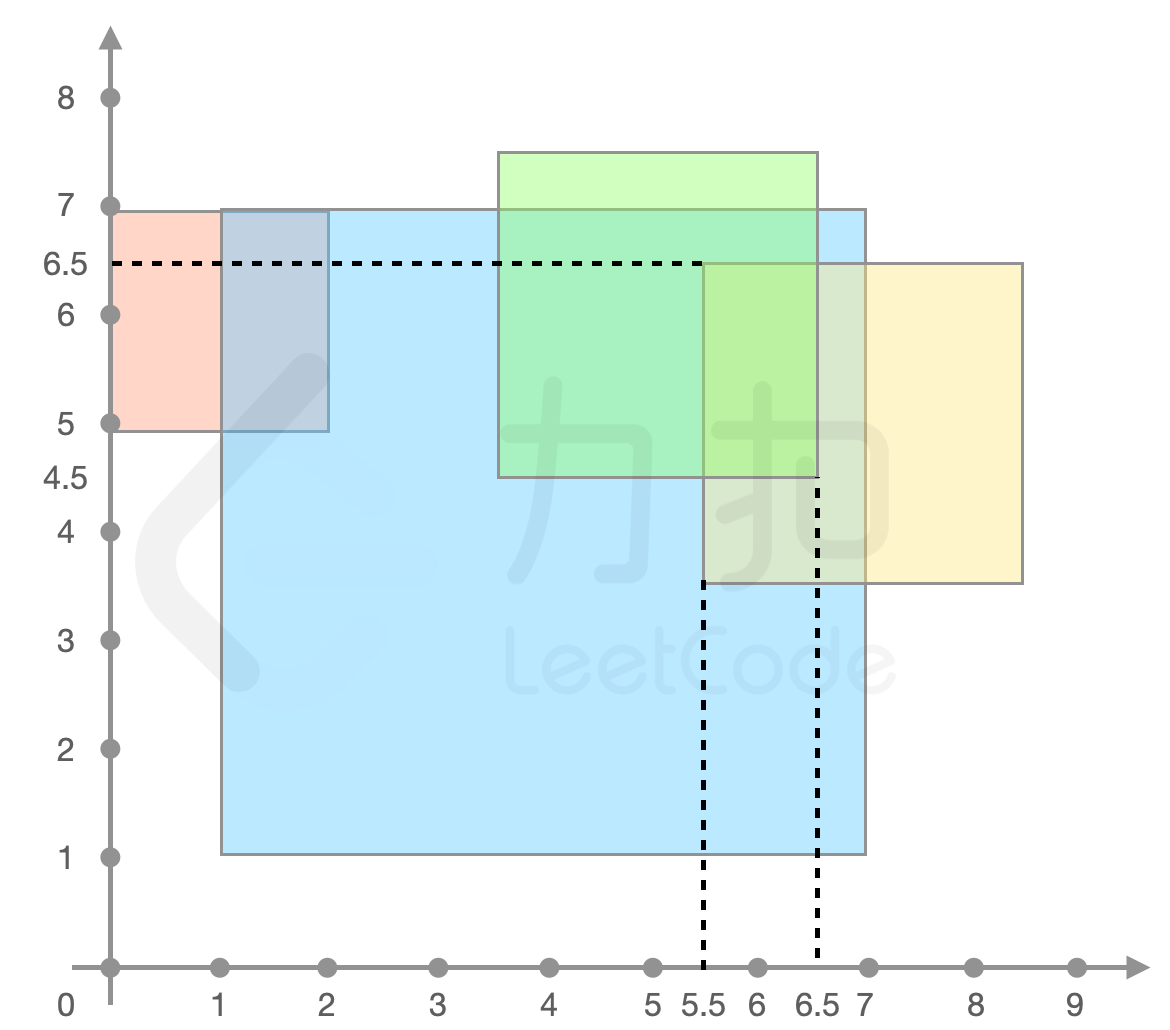
示例 2：

输入：
forceField = [[4,4,6],[7,5,3],[1,6,2],[5,6,3]]

输出：3

解释：如下图所示，
forceField[0]、forceField[1]、forceField[3] 重叠的区域力场强度最大，返回 3

提示：

• 1 <= forceField.length <= 100
• forceField[i].length == 3
• 0 <= forceField[i][0], forceField[i][1] <= 10^9
• 1 <= forceField[i][2] <= 10^9

难度困难5

随着不断的深入，小扣来到了守护者之森寻找的魔法水晶。首先，他必须先通过守护者的考验。

考验的区域是一个正方形的迷宫，maze[i][j] 表示在迷宫 i 行 j 列的地形：

• 若为 . ，表示可以到达的空地；
• 若为 # ，表示不可到达的墙壁；
• 若为 S ，表示小扣的初始位置；
• 若为 T ，表示魔法水晶的位置。

小扣每次可以向 上、下、左、右 相邻的位置移动一格。而守护者拥有一份「传送魔法卷轴」，使用规则如下：

• 魔法需要在小扣位于 空地 时才能释放，发动后卷轴消失；；
• 发动后，小扣会被传送到水平或者竖直的镜像位置，且目标位置不得为墙壁(如下图所示)；
  

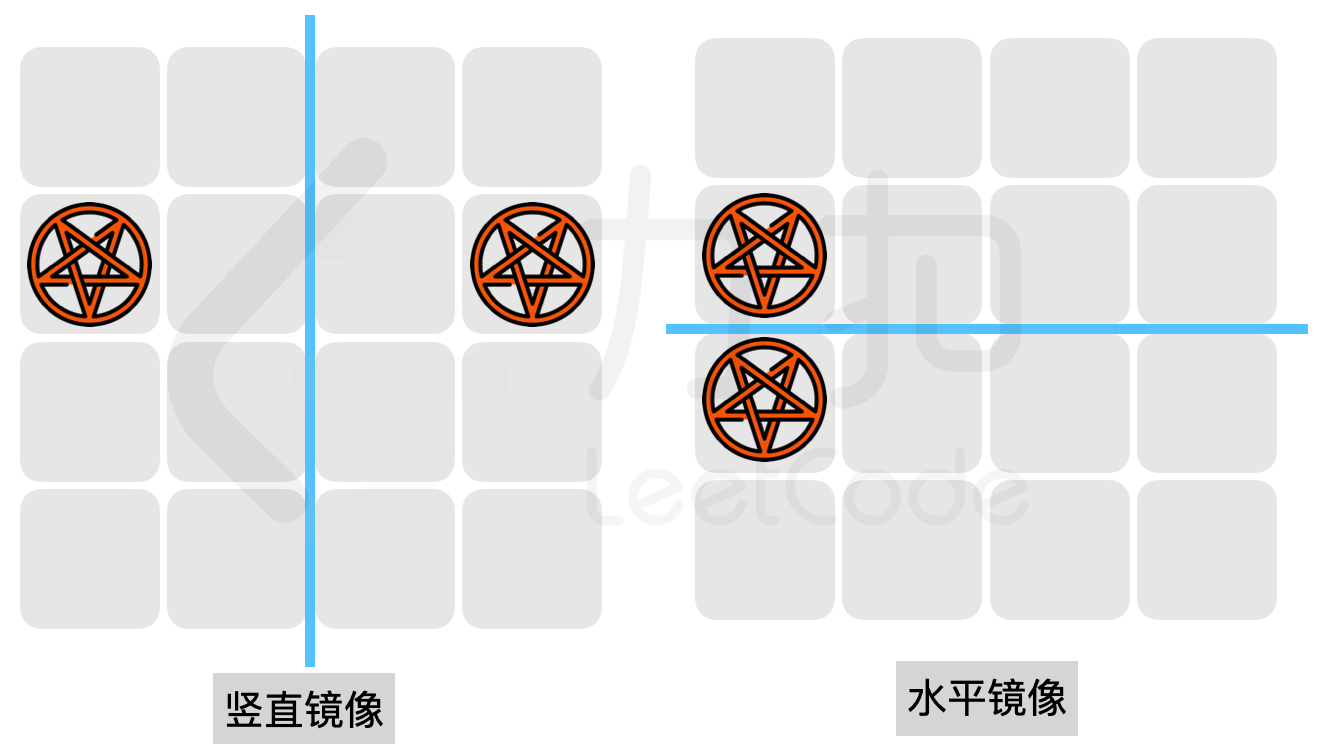
在使用卷轴后，小扣将被「附加负面效果」，因此小扣需要尽可能缩短传送后到达魔法水晶的距离。而守护者的目标是阻止小扣到达魔法水晶的位置；如果无法阻止，则尽可能 增加 小扣传送后到达魔法水晶的距离。
假设小扣和守护者都按最优策略行事，返回小扣需要在 「附加负面效果」的情况下 最少 移动多少次才能到达魔法水晶。如果无法到达，返回 -1。

注意：

• 守护者可以不使用卷轴；
• 传送后的镜像位置可能与原位置相同。

示例 1：

输入：maze = [".....","##S..","...#.","T.#..","###.."]

输出：7

解释：如下图所示：
守护者释放魔法的两个最佳的位置为 [2,0] 或 [3,1]：
若小扣经过 [2,0]，守护者在该位置释放魔法，
小扣被传送至 [2,4] 处且加上负面效果，此时小扣还需要移动 7 次才能到达魔法水晶；
若小扣经过 [3,1]，守护者在该位置释放魔法，
小扣被传送至 [3,3] 处且加上负面效果，此时小扣还需要移动 9 次才能到达魔法水晶；
因此小扣负面效果下最少需要移动 7 次才能到达魔法水晶。

示例 2：

输入：maze = [".#..","..##",".#S.",".#.T"]

输出：-1

解释：如下图所示。
若小扣向下移动至 [3,2]，守护者使其传送至 [0,2]，小扣将无法到达魔法水晶；
若小扣向右移动至 [2,3]，守护者使其传送至 [2,0]，小扣将无法到达魔法水晶；

示例 3：

输入：maze = ["S###.","..###","#..##","##..#","###.T"]

输出：5

解释：如下图所示：
守护者需要小扣在空地才能释放，因此初始无法将其从 [0,0] 传送至 [0,4];
当小扣移动至 [2,1] 时，释放卷轴将其传送至水平方向的镜像位置 [2,1]（为原位置）
而后小扣需要移动 5 次到达魔法水晶

提示：

• 4 <= maze.length == maze[i].length <= 200
• maze[i][j] 仅包含 "."、"#"、"S"、"T"

class Solution:
    """
    什么时候 -1?
    1. 本来就无法到达终点
    2. 无论怎么走，都会被传送到一个无法到达终点的位置

    能不能二分答案?maxDis limit
    为什么可以二分?

    走到一个位置(陷阱) ，传送之后还需要走 > maxDis 步
        如果在不走 # 不走陷阱的情况下，可以到达终点 => 答案 <= maxDis
        如果无法到达终点 => 答案 > maxDis
    答案有单调性，可以二分

    怎么快速判断是否为陷阱:求出终点到其余点的最短路(求各点到终点的最短路不好求，正难则反)


    """
    def challengeOfTheKeeper(self, maze: List[str]) -> int:
        m, n = len(maze), len(maze[0])

        # 1. 找 S T的位置
        for i, row in enumerate(maze):
            for j, c in enumerate(row):
                if c == 'S':
                    sx, sy = i, j
                elif c == 'T':
                    tx, ty = i, j
        
        # 2. BFS求终点到其余点的最短路的长度
        dis_from_t = [[inf] * n for _ in range(m)]
        dis_from_t[tx][ty] = 0
        q = [(tx, ty)]
        step = 1
        while q:
            nxt = []
            for i, j in q:
                for x, y in (i+1, j), (i-1, j), (i, j+1), (i, j-1):
                    if 0 <= x < m and 0 <= y < n and maze[x][y] != '#' and dis_from_t[x][y] == inf:
                        dis_from_t[x][y] = step
                        nxt.append((x, y))
            q = nxt
            step += 1
        
        # 3. 剪枝，如果S无法到达T，直接返回 -1
        if dis_from_t[sx][sy] == inf:
            return -1

        # 4. 二分答案
        vis = [[-1] * n for _ in range(m)]
        def check(max_dis: int) -> bool:
            # DFS，看能否在「附加负面效果」的情况下，移动不超过 max_dis 步到达终点
            def dfs(i: int, j: int) -> bool:
                if i < 0 or i >= m or j < 0 or j >= n or vis[i][j] == max_dis or maze[i][j] == '#':
                    return False
                if maze[i][j] == 'T':  # 到达终点
                    return True
                
                vis[i][j] = max_dis  # 为避免反复创建 vis，用一个每次二分都不一样的数来标记
                # 守护者使用卷轴传送小扣，如果小扣无法在 maxDis 步内到达终点，则返回 false

                # maze[i][n - 1 - j]和maze[m - 1 - i][j] 是 陷阱位置 且 最后不能走到t，return false
                if maze[i][j] == '.' and \
                   (maze[i][n - 1 - j] != '#' and dis_from_t[i][n - 1 - j] > max_dis or
                    maze[m - 1 - i][j] != '#' and dis_from_t[m - 1 - i][j] > max_dis):
                    return False
                for x, y in (i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1):
                    if dfs(x, y):
                        return True
                return False
            return dfs(sx, sy) # 从起点开始走看能不能在移动不超过max_ids步的前提下到达终点
        
        ans = bisect_left(range(m * n + 1), True, key=check)
        return -1 if ans > m * n else ans

难度困难0

在大小为 n * m 的棋盘中，有两种不同的棋子：黑色，红色。当两颗颜色不同的棋子同时满足以下两种情况时，将会产生魔法共鸣：

• 两颗异色棋子在同一行或者同一列

• 两颗异色棋子之间恰好只有一颗棋子

  注：异色棋子之间可以有空位

由于棋盘上被施加了魔法禁制，棋盘上的部分格子变成问号。chessboard[i][j] 表示棋盘第 i 行 j 列的状态：

• 若为 . ，表示当前格子确定为空
• 若为 B ，表示当前格子确定为 黑棋
• 若为 R ，表示当前格子确定为 红棋
• 若为 ? ，表示当前格子待定

现在，探险家小扣的任务是确定所有问号位置的状态（留空/放黑棋/放红棋），使最终的棋盘上，任意两颗棋子间都 无法 产生共鸣。请返回可以满足上述条件的放置方案数量。

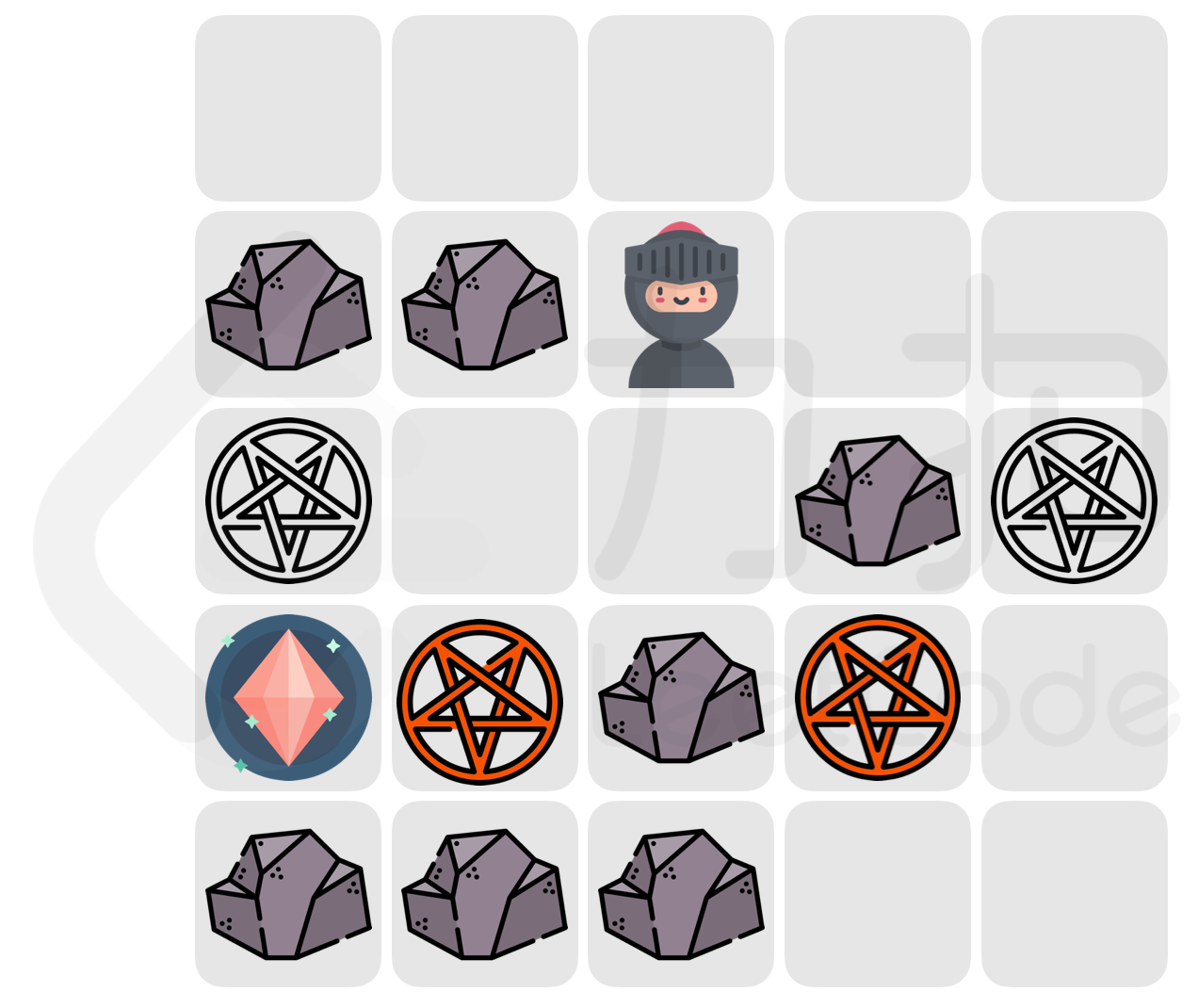
示例1：

输入：n = 3, m = 3, chessboard = ["..R","..B","?R?"]

输出：5

解释：给定的棋盘如图：

所有符合题意的最终局面如图：

示例2：

输入：n = 3, m = 3, chessboard = ["?R?","B?B","?R?"]

输出：105

提示：

• n == chessboard.length
• m == chessboard[i].length
• 1 <= n*m <= 30
• chessboard 中仅包含 "."、"B"、"R"、"?"

不会.jpg
的状态（留空/放黑棋/放红棋），使最终的棋盘上，任意两颗棋子间都 无法 产生共鸣。请返回可以满足上述条件的放置方案数量。

示例1：

输入：n = 3, m = 3, chessboard = ["..R","..B","?R?"]

输出：5

解释：给定的棋盘如图：
[外链图片转存中…(img-MjLgrXnq-1682760441407)]
所有符合题意的最终局面如图：
[外链图片转存中…(img-ADKaCrLh-1682760441408)]

示例2：

输入：n = 3, m = 3, chessboard = ["?R?","B?B","?R?"]

输出：105

提示：

• n == chessboard.length
• m == chessboard[i].length
• 1 <= n*m <= 30
• chessboard 中仅包含 "."、"B"、"R"、"?"

不会.jpg