前言：

作者正好因为动画、模拟仿真等等的重大需求需要预先研发离散形的模型Mesh的形变算法，并且要验证、研究适用的范围、特别是性能等等，摸着石头过河别喷，毕竟我主要是渲染、动画、引擎的对于计算几何、三维重建不是很熟悉，特别是对于一些动画的形变。
对于一个三角形网格的 变形(Deformation) 算法应该满足下面两个基本条件

1. 能够隐藏于交互界面之后
2. 效率足够高以满足交互需求

对于形变根据《Polygon mesh processing》第九章形变的描述，形变大体分为了两种：

1. 空间变形(Space Deformations)：即对曲面的变形是隐式的。因为计算不依赖于三角形网格曲面S，所以其不受网格复杂度和质量的影响；例如FFD算法。
2. **基于曲面的变形(Surface-Based Deformations)：**即计算时在三角形网格上进行的。这类方法能够有很高的控制度，能够对每一个顶点都加以控制，但是其鲁棒性不好，运行效率往往取决网格的的复杂度和质量；例如大名鼎鼎的也是最基础的表面形变“拉普拉斯新形变”、ARAP形变等等。

静态FFD算法：

基础理论：贝塞尔曲线、曲面、超曲面 ；特别注意B样条曲线实际上是对贝塞尔曲线的扩展, B指Basic, 或者说贝塞尔曲线是B样条曲线的特例, B样条曲线通过一系列范围有限的基函数组合来解决贝塞尔曲线牵一发而动全身的缺点。

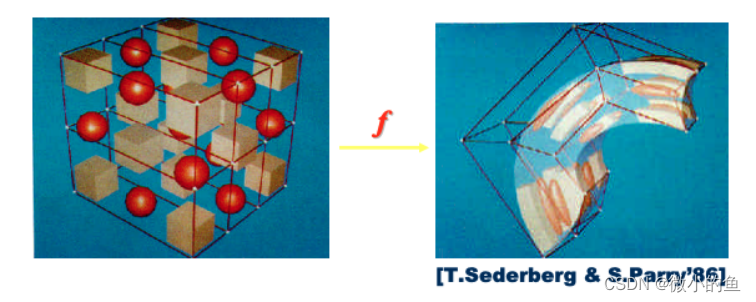
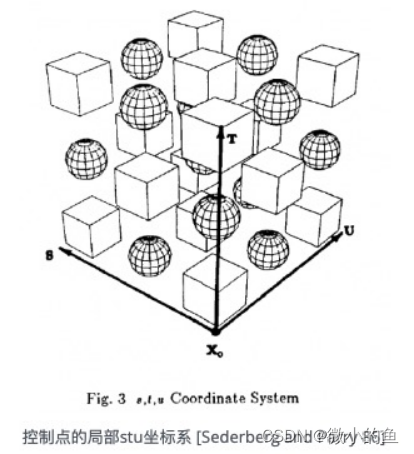
经典控制点形变算法FFDs，经典FFD算法在Blender中主要应用于晶格修改器；

FFD是基于一个3次的贝塞尔超曲面插值或者3次的三次样条插值
而言的：

• 在平行六面体上定义局部坐标系；
• 计算平行六面体中任意点的 (s,t,u) 坐标。
• 在平行六面体上有一个控制点P（l，m，n）来控制网格网格。
• 到处移动控制点P，引起物体形变。
• 基于贝塞尔超曲（B样条线的基函数，）或其他类型的多项式获取到新位置。

STU坐标系中的一点：

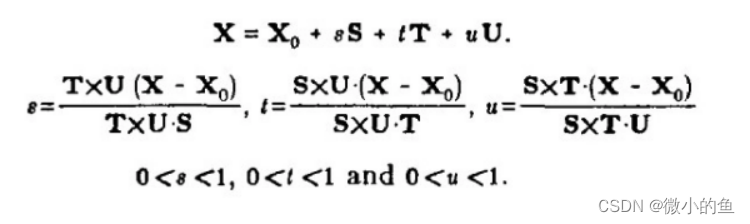
变形点：

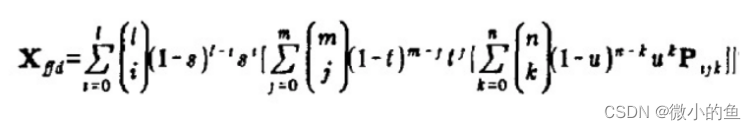
FFD 缺点

• 平行六面体网格形状限制变形形状，控制点不能是任意的。
• 无法控制控制点的在空间中随意分布。
• 贝塞尔基函数具有全局影响力，影响Mesh。
• 晶格边界处变形空间的不连续性，重叠晶格该如何使空间变形？

所以为了解决这些进行了扩展：

- B 样条基 FFD (Purgathofer)。
- 扩展 FFD (Coquillart)
- deCasteljau FFD（Chang & Rockwood）
- Catmull-Clark FFD (McCracken & Joy)
- Dirichlet FFD（Moccozet 和 Thalmann）

即使是用来FFD的扩展与变形还是存在

“如果给定某点位移作为限制条件，其结果会有缺陷。我们假定有N个控制点，M个约束坐标点。这M个点的位移大小我们给出了限定，但我们不知道控制点如何位移才能得到这M个点！”

的问题。

结论：每一个模型顶点都可以通过控制点位置的加权得出。每个控制点对每个顶点的权重，取决于顶点在控制点坐标系下的坐标（形变权重仍然只与位置相关），在经典FFD中是一个B样条基函数的权重。因为权重只取决于初始几何位置，可以预先计算，因此变形时计算很快。 但是不适合进行精细的调整,只能够大范围地进行改动。 对于虚拟衣服来说,这样很容易造成角色衣服失真;并且无法判断某个角点 与实际变形效果的映射关系。

附上Static Bezier 函数生成器FFD的代码实现。

Radial basis function算法

径向基函数（RBF）基础理论：是一个取值仅依赖于到原点距离的实值函数（函数值是“实数”，不可以取虚数或±∞的）也可以按到某一中心点c的距离来定义，其中，函数范式一般为欧几里得距离，不过亦可使用其他距离函数，可以用于许多向函基数的和来逼近某一给定的函数。

RBF形变不需要构建额外的骨骼关节,而是 采用调整自定义控制点的方式来调整附近模型顶点的位置, 控制方法简单,适合自动化处理。并且没有FFD的约束只能较大面积，又有精细度控制点任意非常满足我们低模控制高模的衣服需求。

算法原理：
RBF就是一个方程组的求解，假设在 3 维空间中有 M 个离散点 xi,那么 RBF 可以提供该离散空间中的整体平滑插值函数 F( x) 。 该函数 就是 M 个径向基函数 G(ri)的结果之和,其中 ri 是估算点和 原始点的距离:

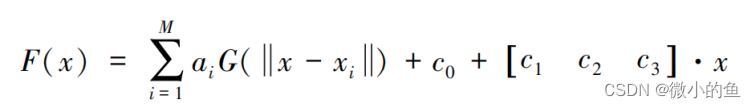
其中 ai 是常量系数,c0 ,c1 ,c2 ,c3 为多项式系数。 因为已知 M 个离散控制点 X1 到 XM ,因此可以构建 M 个 F(Xi)= Fi。 由 此可以构建 M+4 个线性方程组 F=GA 并求解,这里 F= (F1 , F2 , …, FM , 0, 0, 0, 0) ,A = ( a1 , a2 , …, aM , c0 , c1 , c2 , c3 ) ,而 G 是一个(M+4, M+4)的矩阵。解算线性方程组得到所有参数之后,再传入新的 X= ( x, y, z)坐标值,就可以得到对应的空间基函数插值的结果。
RBF的性能在计算的过程需要求取输入点（衣服高模1W+顶点）和所有控制点（人体低模400+）的距离值,因此控制点、求解点的数量会影响到计算的效率;而模型完成变形之后也需要一个后处理的流程来重新计算顶点法线不然影响模型拓扑结构与渲染正确性！

算法性能验证:径向基函数（RBF）的模拟实验下载安装PyGeM看第四节 RBF在houdini的模拟，我这里由于没使用过houdini、并且也是不免费的，但是认识有人研究使用踩坑过，即使人体低模约400+顶点，但是几百个point的rbf跑control point依旧卡上天！根本不是用来跑runtime的方案，只是用来做mesh形变单帧迁移的。PC（I9 9900k）上用dcc跑runtime都卡；maya的例子也有RBF的MayaPlugins，如下图400 控制 6000顶点 ，PC的电脑I7 9700KF。

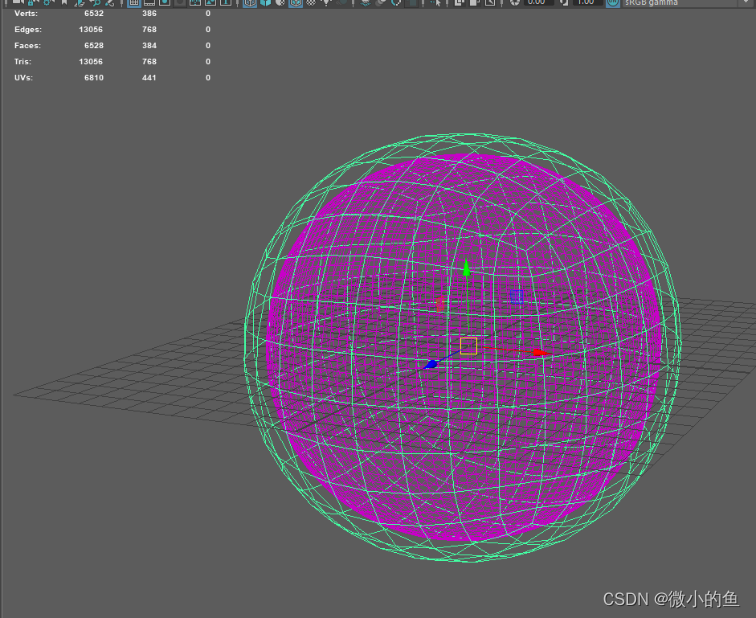
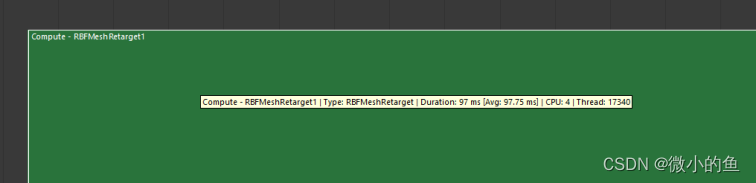
Wrap算法原理：

其操纵Mesh形变影响另一Mesh形变

• D：需要包裹算法变形器修改的网格。
• R：克隆生成D的副本。
• r：网格周围的受影响半径。
• local：控制变形局部的标量。
• f：

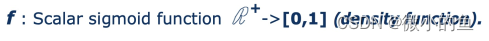
算法绑定：模型R有一个控制点K，模型点P处受包裹算法影响的权重函数F(P,k)=F(dist(P,k))local,P在控制点k的局部坐标系中计算。
形变：网格D的每个顶点都是控制点k。当P绑定到控制点时，P的计算是基于局部坐标系；P点的整体变形是所有控制顶点基于其影响变形函数的加权平均值。

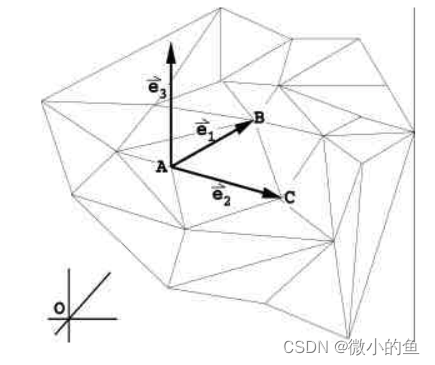
后面介绍的两种形变都是Triangulated Surface Mesh Deformation。

简单的拉普拉斯形变：

Mesh Deformation with Laplacian coordinates（Laplacian Deformation），之前提到的FFD是基于自由形变，而表面形变是微分形变，后者想要求解稀疏矩阵。 拉普拉斯网格变形的本质是网格模型局部细节特征的编码和解码的过程。编码过程是指顶点的欧氏空间坐标到Laplacian坐标的转换。Laplacian坐标包含了网格的局部细节特征，因此Laplacian网格变形算法能够较好地保持网格模型的局部细节。解码过程是指通过微分坐标反求欧氏空间坐标，实质上是一个求解线性系统的过程。拉普拉斯给定具有n个顶点的三角网格模型M=(V,E,F),V为顶点集，E为边集，F为三角面片集合，顶点V与相临顶点的集合vi处的拉普拉斯坐标为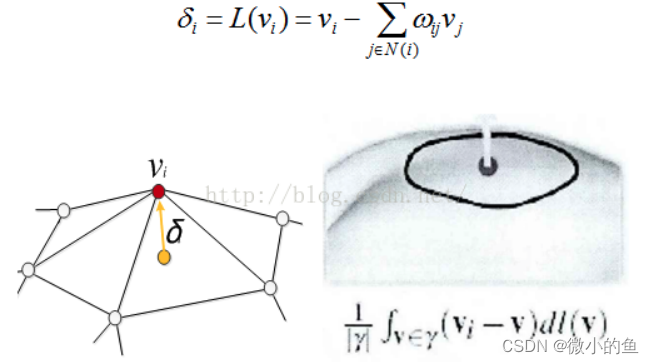
其中,δi为顶点vi的拉普拉斯坐标，L(·)为网格的拉普拉斯算子，ωij为vj点相对于vi点的权值，且∑ωij=1。权重使用基于余切的权重（cotangent权重）即边的两个邻接三角面片的对角的余切的均值：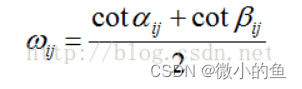

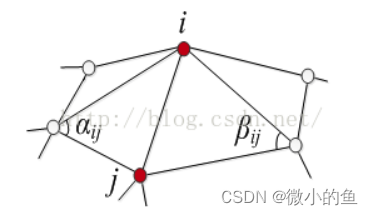
使用余切权重，这种变形方法能尽可能的保留局部细节。拉普拉斯具有三个性质：线性变换、平移不变性、旋转变换敏感
根据拉普拉斯坐标的性质，其对旋转敏感，所以网格的局部信息会发生旋转扭曲，且旋转尺度较大是，扭曲会非常严重就会失真。要实现网格模型的保特征变形，不能直接使用原网格的拉普拉斯坐标来重建变形后的网格模型，而应该重新设置微分坐标的方向再重建模型。

详细请看：图形处理（三）简单拉普拉斯网格变形-Siggraph 2004_hjimce的博客-CSDN博客
或者 ： 用数学编辑3D模型（一）- Mesh Deformation with Laplacian Coordinates - 知乎

As-Rigid-As-Possible 算法

ARAP算法原理及其详解请看参考【5】与【6】
ARAP算法能“在保持局部细节的前提下去编辑模型的大体形态”这一要求，而且易于实现，计算量较小，并且算法保证会收敛。但是，ARAP也存在诸如无法保持模型的体积，以及当模型很精细时解算会不太稳定等缺陷，

最重点的是地下cgal的算法实现：
添CGAL 表面形变使用（拉普拉斯、ARAP形变）教程；

参考资料：

1.形变FFDs, wires, wraps论文
2.计算机图形学十：贝塞尔曲线与贝塞尔曲面 - 知乎
3.径向基函数RBF三维网格变形
4、模型变形从FFD到RBF
5、用数学编辑3D模型（二）- As-Rigid-As-Possible
6、动画形变Linear rotation-invariant coordinates和As-Rigid-As-Possible算法