4 反向传播求梯度🥥

4.1 简介

上一篇：【一起撸个DL框架】3 前向传播

前面我们已经介绍了前向传播，而本节即将介绍的反向传播中的自动微分机制，可以说是深度学习框架的一个核心功能。因为计算图中的参数正是按照着梯度的指引来更新的。

4.2 导数与梯度

说到“梯度”与“导数”这两个概念，有些同学可能已经有些模糊了。在一元函数的情况下，两者几乎可以混为一谈，然而在多元函数的情况下梯度与导数的概念是有区别的。例如二元函数 $f (x, y)$ ，

它沿着二维平面内的每一个方向都会有一个方向导数，方向导数的结果是一个数值，代表沿着该方向的变化率；
而它只有一个梯度，梯度的结果是一个向量， $\triangledown f(x,y)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$ ，它同时指示了两个信息：变化率最大的方向和相应的变化率。

4.3 链式法则

简单描述就是“嵌套函数的导，等于各层求导的乘积”。下面是数学的表达： $z = f (y), y = g (x)$ ，则 $\frac{\partial z}{\partial x}=\frac{\partial z}{\partial y} \frac{\partial y}{\partial x}$ 。计算图就相当于多层的嵌套函数，线性函数可以表示成加法和乘法节点的嵌套。

problem: 梯度不是相对于函数而言的吗？例如 $\triangledown f(w,x)$ 。为什么会有“w的梯度”这种概念呢？

在计算图中求一个节点的梯度，只需要将结果节点对子节点的梯度与子节点对自己的梯度乘起来就可以了。


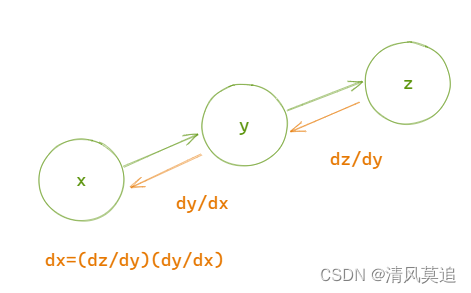图1：链式法则

4.4 示例：y=2x+1的梯度

为了实现反向传播，我们需要在节点类中加入几个方法。

class Node:
    def __init__(self, parent1=None, parent2=None) -> None:
        self.parent1 = parent1
        self.parent2 = parent2
        self.value = None

        self.grad = None  # 在其它结点求梯度时可能再次用到本结点的梯度
        self.children = []

        parents = [self.parent1, self.parent2]
        for parent in parents:
            if parent is not None:
                parent.children.append(self)

    def set_value(self, value):
        self.value = value
    def compute(self):
        '''抽象方法，在具体的类中重写'''
        pass
    def forward(self):
        for parent in [self.parent1, self.parent2]:
            if parent.value is None:
                parent.forward()
        self.compute()
        return self.value
    def get_parent_grad(self, parent):
        '''求本节点对于父节点的梯度，抽象方法'''
        pass
    def get_grad(self):
        '''求结果节点对本节点的梯度'''
        # 结果结点返回单位值，而不是self.value
        if not self.children:
            return 1
        if self.grad is not None:
            return self.grad
        else:
            self.grad = 0
            for i in range(len(self.children)):
                grad1 = self.children[i].get_parent_grad(parent=self)  # 子节点对自己的梯度
                grad2 = self.children[i].get_grad()  # 结果节点对子节点的梯度
                self.grad += grad1 * grad2
            return self.grad


class Varrible(Node):
    def __init__(self) -> None:
        super().__init__()

class Add(Node):
    def __init__(self, parent1=None, parent2=None) -> None:
        super().__init__(parent1, parent2)
    def compute(self):
        self.value = self.parent1.value + self.parent2.value
    def get_parent_grad(self, parent):
        return 1

class Mul(Node):
    def __init__(self, parent1=None, parent2=None) -> None:
        super().__init__(parent1, parent2)
    def compute(self):
        self.value = self.parent1.value * self.parent2.value
    def get_parent_grad(self, parent):
        '''从parent1,2改成parents时，需要重写'''
        if parent == self.parent1:
            return self.parent2.value
        elif parent == self.parent2:
            return self.parent1.value
        else:
            raise "get which is not a parent of mul node"

在之前的基础上，我们在Node类中新增了两个属性self.grad和self.children，它们都将在get_grad()方法中发挥作用。

然后我们还在Node类中新增了两个方get_parent_grad()和get_grad()，分别用来求子节点对于子节点的父节点（即本节点）的梯度，和结果节点对于本节点的梯度。get_parent_grad()是一个抽象方法，还需在Add类和Mul类中进行具体的实现，实现的方式比较简单，大家阅读源代码即可。

关于get_grad()方法，在本节点没有子节点时，就判断本节点为结果节点，梯度设置为单位值1。在本节点梯度已经存在时，就不再进行递归求值，而直接返回已经保存的梯度值。为什么要保存梯度值？一个节点可以有多个需要求梯度的父节点，这种情况下就会多次用到同一个节点的梯度，每次都递归到结果节点来求值显然是不必要的，于是我们使用空间来换时间。

在下面的示例代码中，我们求 $w$ 和 $x$ 的梯度，就两次用到了mul节点的梯度。

if __name__ == '__main__':
    # 搭建计算图: y=2x+1
    x1 = od.core.Varrible()
    w1 = od.core.Varrible()
    mul = od.ops.Mul(x1, w1)
    b = od.core.Varrible()
    add = od.ops.Add(mul, b)
    # 给参数赋值
    w1.set_value(2)
    b.set_value(1)
    # 使用计算图计算
    x1.set_value(int(input("请输入x：")))
    y = add.forward()
    print(f"y: {y}")
    # 反向传播求梯度
    w_grad = w1.get_grad()
    x_grad = x1.get_grad()
    print(f"w_grad: {w_grad}, x_grad: {x_grad}")

    '''
    请输入x：3
    y: 7
    w_grad: 3, x_grad: 2
    '''