一.密码学
密码学中常见的加密方式可以分为两类:对称加密和非对称加密。
对称加密:对称加密采用相同的密钥来进行加密和解密。因为加密和解密都使用同样的密钥,所以对称加密速度快、效率高,但在密钥管理方面存在困难。常见的对称加密算法有 DES、3DES、AES 等。
非对称加密:非对称加密采用不同的密钥来进行加密和解密。公钥可以自由地分发给任何需要加密的人,但只有拥有相应私钥的人才能解密信息。非对称加密算法常见的有 RSA、DSA 和 ECC 等。
除了对称加密和非对称加密之外,还有哈希函数、消息认证码(MAC)、数字签名等其他密码学技术。哈希函数是将任意长度的消息转换成固定长度的摘要值的方法;MAC 是将消息和密钥混合计算出一段密文作为认证码的方法;数字签名则是通过非对称加密来确保消息的完整性、真实性和不可抵赖性的方法。
这里我们只讨论前面两种常见的加密算法。
二.非对称加密
非对称加密是一种加密方式,与对称加密不同,它使用了一对密钥:公钥和私钥。公钥可以自由地分发给任何需要加密的人,但只有拥有相应私钥的人才能解密信息。
在非对称加密中,使用公钥进行加密操作,而使用私钥进行解密操作。发送方将要传输的数据使用接收方的公钥进行加密,只有接收方拥有相应的私钥才能解密并读取该数据。
非对称加密算法常见的有 RSA、DSA 和 ECC 等。它们广泛应用于数字证书、数字签名、安全电子邮件等领域,并被作为 HTTPS、SSH、SSL/TLS 等协议的基础加密机制。
本次实验用RSA算法模拟非对称加密通信过程。
三.RSA算法
RSA 算法是一种非对称加密算法,它可以用于保护数字通信的机密性和完整性。RSA 算法是由三位数学家(Rivest、Shamir 和 Adleman)在 1977 年提出的,取名来自他们的姓氏首字母。
RSA 算法的关键在于使用了两个大素数,并将其乘积作为公开的密钥中的一个参数,而这两个大素数只有私钥持有者才知道。计算机很容易地进行大数相乘,但却难以从乘积中分解出两个大素数。因此,如果某个人要发送加密信息给另一个人,则需要使用接收方的公钥对信息进行加密,只有接收方才能使用他们拥有的私钥进行解密。
RSA 算法的安全性基于大数分解问题,即寻找两个大质数的乘积。目前,没有已知的快速算法可以有效地解决大数分解问题,因此 RSA 算法被认为是一种安全可靠的加密技术。
除了保证机密性,RSA 算法还可以用于数字签名、密钥交换等领域。例如,在数字签名中,发送方可以使用自己的私钥对消息进行签名,接收方则使用发送方的公钥来验证签名是否有效。在密钥交换中,双方可以使用 RSA 算法来协商出一个会话密钥,从而实现对称加密方式的安全通信。
RSA用数字前面进行身份验证,这是我下一篇博客的内容。
四.基本步骤
以下是一个使用RSA算法加密明文"abcdefg"的例子,并简述加密过程:
- 选择两个大素数p和q。假设选择的素数为p=11和q=17。
- 计算n=p*q,得到n=187。
- 计算欧拉函数φ(n)=(p-1)(q-1),得到φ(n)=160。
- 选择一个与φ(n)互质的正整数e。通常可以选择65537作为公钥指数e。
- 计算e模φ(n)的逆元d,即d*e ≡ 1 mod φ(n)。这里可以使用扩展欧几里得算法计算,得到d=7937。
- 公钥为(n,e)=(187,65537),私钥为d=7937。
- 将明文"abcdefg"转换为数字形式,例如使用ASCII码转换,得到数字序列a=97, b=98, c=99, d=100, e=101, f=102, g=103。
- 对于每一个数字ai,使用公钥进行加密。加密过程为ci = ai^e mod n。
- 得到密文序列c={423, 130, 58, 66, 108, 61, 133}。
- 将密文序列c发送给接收者。
- 接收者使用私钥对密文进行解密。对于每一个密文ci,使用私钥进行解密。解密过程为ai = ci^d mod n。
- 得到原始数字序列a={97, 98, 99, 100, 101, 102, 103},即明文"abcdefg"。
在上述过程中,公钥和私钥的生成使用了RSA算法,加密过程使用了公钥进行加密,解密过程使用了私钥进行解密。需要注意的是,在实际应用中,还需要考虑其他因素,例如数据块长度、填充方式、数字签名等,以保证加密通信的安全性和完整性。
五.python代码实现
import random
import base64
# 定义一个函数用于生成指定位数的素数
def creat_number(num1,num2):
while True:
p = random.randint(num1,num2) #随机产生一个指定位数的整数
if checknum(p):
return p
#一直while循环,直到产生的数是素数
# 判断是否为素数
def checknum(n):
if n < 2:
return False
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return False
#如果循环结束还没有数与之整除,这个数就是素数
return True
# 计算扩展欧几里得算法(求逆元)
def niyuan(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = niyuan(b % a, a)
return (g, x - (b // a) * y, y)
#参数a:模数,参数b:需求逆元的数,返回值中g是a和b的最大公约数,x - (b // a) * y这个式子的值就是我们所求的逆元
#产生公钥和私钥函数
def creatkey(p,q):
n=p*q #计算n=p*q
ln=(p-1)*(q-1) # 计算φ(n) = (p-1) * (q-1)
e = 65537 # 选择一个与ln互质的整数e作为公钥指数,一般都选取65537相当于约定俗成
# 计算d = e^(-1) mod ln,即e模ln的逆元
_, d, _ = niyuan(e, ln)
# 确保d在合法范围内(1 < d < ln)
d = d % ln
if d <= 1:
d += ln
# 返回公钥(n, e)和私钥d
return n, e, d
#加密函数
def encrypt(message, n, e):
print("Alice发送使用公钥加密后的密文为:", end='')
encrypted_list = []
for char in message:
encrypted_num = pow(ord(char), e, n) #利用pow函数进行RSA加密
encrypted_char = chr(encrypted_num) #转化为ASCll字符
encrypted_list.append(encrypted_char) #存入列表
encrypted_message = ''.join(encrypted_list) #拼接成一个字符串
# 进行 Base64 编码
base64_data = base64.b64encode(encrypted_message.encode('utf-8')).decode('ascii')
print(base64_data) #编码结果即密文
return base64_data
#解密函数
def decrypt(value,n,d):
print("Bob收到Alice发送的密文:",end='')
print(value)
# 进行 Base64 解码
binary_data = base64.b64decode(value) #解码得到二进制数字
binary_string = binary_data.decode('utf-8') #换成ASCll字符串
decrypted_list = []
for i in range(len(binary_string)):
decrypted_num = pow(ord(binary_string[i]), d, n) #利用pow函数进行RSA解密
decrypted_char = chr(decrypted_num) #换成字符串
decrypted_list.append(decrypted_char)
decrypted_message = ''.join(decrypted_list)
print("Bob利用私钥解密结果为:",end='')
print(decrypted_message)
#测试代码
a=input("请输入产生素数的范围起点:")
num1=int(a)
b=input("请输入产生素数的范围终点:")
num2=int(b)
p=creat_number(num1,num2)
q=creat_number(num1,num2)
c=input("请输入Alice要发送给Bob的明文:")
str1=list(c)
n,e,d=creatkey(p,q)
str2=encrypt(str1,n,e)
print("------------------")
decrypt(str2,n,d)
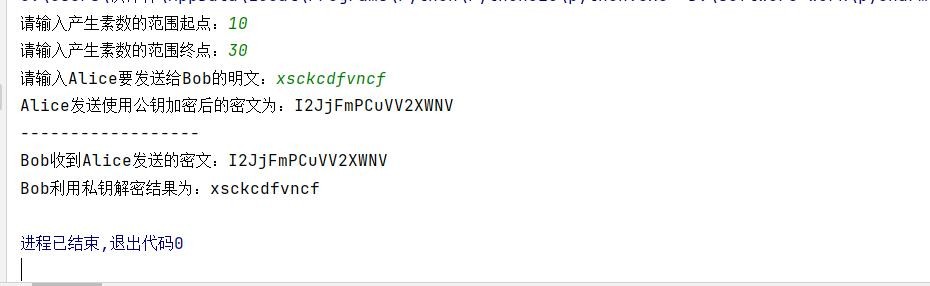
六.运行结果
如果你想了解对称加密,可以参考:
对称加密之移位密码
对称加密之仿射密码
对称加密之Hill密码

![[2021.11.9]lighteffect架构优化详细设计文档](https://img-blog.csdnimg.cn/b53a6e66ede848ea85d5a4c8a4570bfa.png)