【算法】欧拉路径的DFS存储顺序

news2024/11/24 14:37:26

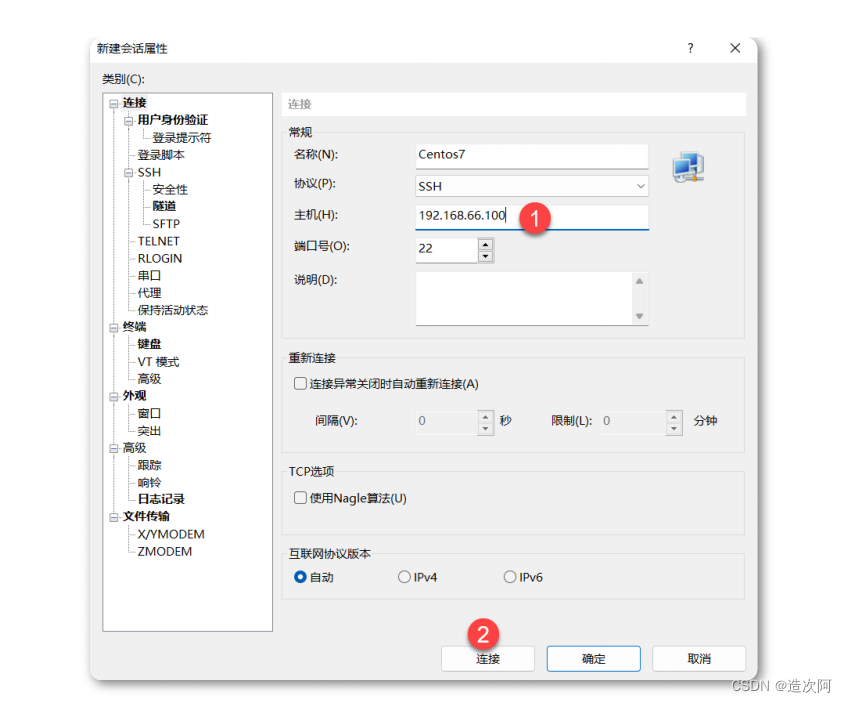
欧拉路径和欧拉回路

  • 对于无向图，所有边都是连通的。

    （1）存在欧拉路径的充分必要条件：度数为奇数的点只能有0个或2个。

    （2）存在欧拉回路的充分必要条件：度数为奇数的点只能有0个。

  • 对于有向图，所有边都是连通。

    （1）存在欧拉路径的充分必要条件：要么所有的点出度均等于入度；要么除了两个点之外，其余所有点的出度等于入度，剩余的两个点：一个满足出度比入度多1（起点），一个满足入度比出度为1（终点）。

    （2）存在欧拉回路的充分必要条件：所有点的出度均等于入度。

随记：

在学习过程中，有几个困扰我的点，这里列一下方便回忆。
欧拉路径有如下两种形式，其余各种各样的形式都可以简化成这两种。

在这里插入图片描述

深搜加入边的顺序

在 dfs 过程中，从起点出发深搜，第一次回溯的地方必定是终点。在深搜过程中，需要将遍历过的边及时删除，防止重复遍历，复杂度退化成 O ( m 2 ) O(m^2) O(m2) 。

以左图为例，如果按照深搜的过程加入所有的深搜到的边，那么这个环未被正常加入。
这里正常加入是指，如果我们回溯到交点处，再去遍历环上的边，这样就不是一笔画了。

按照深搜的顺序结束后再将当前遍历的边加入，一个未得到数学证明的猜想：以这种方式，每个点在你当前 dfs 栈中最多只会拓展 2 次（与这个点相连的边会在这个点的其他 dfs 栈中被遍历到）。

最后得到的是欧拉路径的逆序边，reverse 后即欧拉路径。

假设当前点是 i ，当前遍历的边的另一个点为 j
在执行完 dfs(j) 后，就将对应的边加入栈中。这是因为这里考虑 dfs(j) 是考虑将所有从 j 开始的边都遍历完毕。
如此，这条 i->j 的边就是当前顺序中遍历的最靠后的边。

故在加入边时，在每次 dfs 后就将这条边加入栈中，这是正确的。

深搜加入点的顺序

点的序列表示欧拉路径，路径中连续的两个点即表示一条边，故 点数 = 边数 + 1 。

依旧考虑 dfs 过程。当前点为 i ，而上述说明已经表明了可能会存在一个 dfs 栈中，一个点会遍历至多 2 条边。如果我们在一次 dfs 结束后就加入当前点 i ，看起来是没什么大问题的。

我们来考虑这个例子

n = 3, m = 3

每条边如下：
1 2
1 3
1 3

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1RddoyQ6-1682675405706)(/images/6.png)]

假设起点为 1

  • 首先遍历了1->2 这条边
  • 2 没有其他的边，加入点 2 ，此时序列为 [2]
  • 回溯到 1 ， 此时 dfs(1) 结束了一次，加入点 1，此时序列为 [2,1]
  • 1 继续遍历边 1->3 （两条边随意，对结果不影响）
  • 3 遍历其唯一的一条边 3->1
  • 1 此时没有其他的边，故加入点 1，序列为 [2,1,1]
  • 回溯到 3 ，此时 dfs(3) 结束了一次，加入点 3，此时序列为 [2,1,1,3]
  • 回溯到 1 ，此时 dfs(1) 结束了一次，加入点 1，此时序列为 [2,1,1,3,1]

这里连续两个 1 显然是错误的，说明我们这里加点顺序是有问题的。

那么这里相较于加入边有什么区别呢？再来模拟下加入边的过程：

假设起点为 1

  • 首先遍历了1->2 这条边
  • 2 没有其他的边，结束
  • 回溯到 1 ， 此时 dfs(1) 结束了一次，加入边 1->2，此时序列为 [1->2]
  • 1 继续遍历边 1->3 （两条边随意，对结果不影响）
  • 3 遍历其唯一的一条边 3->1
  • 1 此时没有其他的边，结束
  • 回溯到 3 ，此时 dfs(3) 结束了一次，加入边 3->1，此时序列为 [1->2,3->1]
  • 回溯到 1 ，此时 dfs(1) 结束了一次，加入边 1->3，此时序列为 [1->2,3->1,1->3]

这里的加边序列为：[1->2,3->1,1->3]，即 [2<-1, 1<-3, 3<-1]

上述的加点序列为：[2,1,1,3,1]，正确的加点序列为：[2, 1, 3, 1]

这里问题在于我们多加入了一个 1 ，这两个 1 都是在 dfs 结束的时候加入的，而其他的点加入存在情况为这个点不存在其他的边时，加入这个点。

如果修改为这种情况，再来模拟下加点的过程：

假设起点为 1

  • 首先遍历了1->2 这条边
  • 2 没有其他的边，加入点 2 ，此时序列为 [2]
  • 回溯到 1 ， 此时 dfs(1) 结束了一次
  • 1 继续遍历边 1->3 （两条边随意，对结果不影响）
  • 3 遍历其唯一的一条边 3->1
  • 1 此时没有其他的边，故加入点 1，序列为 [2,1]
  • 回溯到 3 ，3 此时没有其他的边，故加入点 3，序列为 [2,1,3]
  • 回溯到 1 ， 1 此时没有其他的边，故加入点 1，序列为 [2,1,3,1]

如此就是正确的了。

但这里还没有搞清楚加点的具体的含义。

不同于加边，每条边在遍历后立马被删除，所以边在 dfs 完毕后立马加入是可以的。

假设当前点为 vertex，当前遍历完边 edge1，加入 edge1 后，假设当前 dfs 栈还可以遍历一条边 edge2，则说明 edge2 在欧拉路径中，通过 edge2，到达了 vertex，然后再通过 edge1 出去。

对于加点来说，每个点的加入需要斟酌，直观的想法就是按照加边的顺序加点。但是这会存在上述模拟中的情况，多加入了一些点。

之前说过，每个点至多会走两条边 e1 和 e2，这是因为 e1 会走到终点，然后回溯。如果说通过 e1 又可以一直深搜走回这个点，那么这就是一条完整的路径。回溯过程中按照这个顺序加点即可。

考虑两种情况：

  1. 从当前点 vertex 可以直接从一条边出发走完剩余未走的所有边，并且回到 vertex，此时我们只需要在回溯前（return 之前）加点即可。

  2. 从当前点 vertex 从一条边走到了终点，然后需要回溯继续走剩余未走的边。对于从终点回溯到当前点 vertex 的部分，假设这些点已经不存在其他的边了，那么只需要在他们回溯前（return 之前）加点即可。

    这些未走的边，我们继续从 vertex 出发，必然是一个环。因为是从 vertex 继续出发走这个环，必然最后会回到 vertex。考虑一个环的加边顺序，遍历完这个环后，依次回溯加入环的边，对于第一个加入的边，实际上是遍历环结束后到达 vertex 的边，而在正序的欧拉路径中，这条边之后就会继续从 vertex 深搜到终点，所以说，这条边紧接着之后的深搜到终点的路径，对应到这个图上是：从[3->1, 1->2]。

    而这里的 1 只能被加入 1 次，上述错误的加点顺序中，我们在回溯到 vertex 时加入了一次，然后遍历完这个环后回溯又加入了一次，导致这里加入了两次。

    我们需要清楚的是，这里环的回溯第一次加的边 3->1 ，之前加的边为 1->2 ，使得序列变成了 [1->2, 3->1]
    正序欧拉路径即为：[3->1, 1->2]。

    冲突在于：整个欧拉路径用边表示和用点表示的数量关系为：点数 = 边数 + 1，每条边都可以用 到达点 来表示，最后再加上一个整个路径的起点即可。

    所以我们这下清楚了，我们是使用每条边的到达点作为这条边的代表。如此，一个点在一次 dfs 栈中只有一次作为到达点的可能，即这个点遍历完了其所有还存在的边后（此时相当于我将所有其他的环都遍历完了）。因为我这条边先遍历到，那么我就应该最后加入这条边，这样在欧拉路径的顺序才是正确的。

综上：

在回溯前加点，每个点表示的是边对应的到达点。而我们可以认为 dfs(start) 中这个起点 start 也是从某个点过来的，回溯过程中也是最后将其加入欧拉路径中，这样整体的逻辑就说得通了。

总结

在跑欧拉路径时，加边和加点的问题，本质在于这条边是什么边：
假设我们当前在点 a 经过边 edge 到达了点 b，而我们到达 a ，是从 prea 经过 pre_edge 到达了 a

  • 对于加边，我们从 a 经过 edge 到达了 b 后，从 b 出发的所有点遍历完毕后再加入点 a，是指 edge 这条边可以到达的其他边已经结束，而 edge 这条边是我们遍历完其之后的边的起始边。

  • 对于加点，我们从 prea 经过 pre_edge 到达 a，再从 a 开始遍历其所有的边去深搜，深搜结束后，我们再将 prea->a 这条 pre_edge 边加入到序列中，加入的形式是将 a 这个 prea 的到达点加入到序列中。

    我们在调用 dfs(start) 时，可以认为我们是从一个 虚拟点 virtual_vertex 经过虚拟边virtual_edge 到达了 start ，所以这样的话也可以将 start 作为边的到达点了。

故我们的加边和加点顺序为：

  • 对于加边的问题，应该在一次边的 dfs 结束后就将当前遍历走的这条边加入。
  • 对于加点的问题，应该在所有当前点的 dfs 结束后才将当前点 vertex 加入，这个点 vertex 代表的是走到 vertex 这个点的 edge 的到达点。

疑惑

这里不用起点来代表每条边的原因：在 dfs 时，我们并不知道哪个点是终点（并不是所有的欧拉路径都存在两个度为奇数的起点和终点，欧拉回路这种欧拉路径所有的度数都是偶数），但是我们第一次开始 dfs 的点就是起点，最后回溯回来也可以顺利地将其加入欧拉路径的点序列中。

例题1

P7771 【模板】欧拉路径

示例代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
const int M = 200010;
multiset<int> h[N];
int din[N], dout[N];
int ans[M], cnt;
int n, m;

void dfs(int u) {
    while (!h[u].empty()) {
        int v = *h[u].begin();
        h[u].erase(h[u].begin());
        dfs(v);
    }
    ans[++cnt] = u;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        h[a].insert(b);
        dout[a] += 1;
        din[b] += 1;
    }

    int act[2] = {0, 0};
    int start = 0;
    for (int i = 1; i <= n; ++i) {
        if (din[i] == dout[i] + 1) {
            act[0] += 1;
        } else if (dout[i] == din[i] + 1) {
            start = i;
            act[1] += 1;
        } else if (din[i] != dout[i]) {
            puts("No");
            return 0;
        }
    }

    if (act[0] != act[1] || act[0] > 1) {
        puts("No");
        return 0;
    }

    if (start == 0) {
        for (int i = 1; i <= n; ++i) {
            if (dout[i] == din[i] + 1) {
                start = i;
                break;
            } else if (din[i] == dout[i] && start == 0) {
                // 字典序最小，如果不存在 dout[i]==din[i]+1的起点，那么就选择字典序最小的
                start = i;
            }
        }
    }

    dfs(start);

    for (int i = cnt; i >= 1; --i) printf("%d%c", ans[i], " \n"[i == 1]);

    return 0;
}

例题2

1184. 欧拉回路

示例代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
const int M = 400010;

int h[N], e[M], ne[M], idx;
bool used[M];
int ans[M >> 1], cnt;
int din[N], dout[N];
int n, m, type;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u) {
    while (h[u] != -1) {
        // 删边
        int i = h[u];
        h[u] = ne[i];
        
        // 标记用过的边和其反向边，used[i]=true其实用不到了，因为这条边已经被删除了
        if (used[i]) continue ;
//        used[i] = true;
        if (type == 1) used[i ^ 1] = true;

        dfs(e[i]);

        int t = i + 1;
        if (type == 1) {
            t = i / 2 + 1;
            if (i & 1) t = -t;
        }
        ans[++cnt] = t;
    }
}

int main()
{
    scanf("%d", &type);
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);

    for (int i = 1; i <= m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        if (type == 1) add(b, a);
        din[b] += 1;
        dout[a] += 1;
    }

    if (type == 1) {
        for (int i = 1; i <= n; ++i) {
            if ((din[i] + dout[i]) % 2 == 1) {
                puts("NO");
                return 0;
            }
        }
    } else {
        for (int i = 1; i <= n; ++i) {
            if (din[i] != dout[i]) {
                puts("NO");
                return 0;
            }
        }
    }

    for (int i = 1; i <= n; ++i)
        if (h[i] != -1) {
            dfs(i);
            break;
        }

    if (cnt < m) {
        puts("NO");
        return 0;
    }

    puts("YES");
    for (int i = cnt; i >= 1; --i) printf("%d%c", ans[i], " \n"[i == 1]);

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/472430.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

jvm之字节码

jvm之字节码

写在前面 java字节码由单字节的指令(也叫做操作码)组成&#xff0c;但一个 byte 最多能够存储 256 个指令&#xff0c;够用吗&#xff1f;截止到目前是够的&#xff0c;因为指令的个数是200多一点&#xff0c;指令分为如下四类&#xff1a; 1&#xff1a;栈操作指令&#xff…
阅读更多...
【前端基础知识】Vue中的变量不是响应式的吗？属性赋值后视图不变化的原因是什么？

【前端基础知识】Vue中的变量不是响应式的吗？属性赋值后视图不变化的原因是什么？

目录 &#x1f914;问题&#x1f4dd;回答&#x1f3a8;使用场景动态添加属性动态添加数组元素 ❌注意事项$set只能在响应式对象上使用$set不能用于根级别的属性$set的性能问题 &#x1f4c4;总结 &#x1f914;问题 Vue是一款在国内非常流行的框架&#xff0c;采用MVVM架构&a…
阅读更多...
数据库课设--基于Python+MySQL的餐厅点餐系统

数据库课设--基于Python+MySQL的餐厅点餐系统

文章目录 一、系统需求分析二、系统设计1. 功能结构设计2、概念设计2.2.1 bill_food表E-R图2.2.2 bills表E-R图2.2.3 categories E-R图2.2.4 discounts表 E-R图2.2.5 emp表E-R图2.2.6 food 表E-R图2.2.7 member表E-R图2.2.8 member_point_bill表E-R图2.2.9 servers表E-R图2.2.1…
阅读更多...
五一出行！如何辨别偷拍设备

五一出行！如何辨别偷拍设备

五一小长假即将到来&#xff0c;作为出行的重要一环&#xff0c;我们都希望能在旅途中享受安全与便捷。但不可避免的事&#xff0c;有些不法分子可能会通过安装针孔摄像头等方式进行非法监控。从表面上看&#xff0c;我们很难分辨。这些小小的设备&#xff0c;被伪装成日常用品…
阅读更多...
elementUI组件库el-switch开关控件的样式设置，精细至开关内的文字、圆点、背景设置

elementUI组件库el-switch开关控件的样式设置，精细至开关内的文字、圆点、背景设置

开发项目时做一种开关控件样式&#xff0c;要求显示和隐藏两种状态下的文字、圆点、背景色等都有区别&#xff0c;就研究了一下&#xff0c;各种设置已在代码中标注&#xff0c;小白也可直接复制使用。 <el-table-column label"操作"><template slot-scope&…
阅读更多...
【FPGA】Spartan®-7器件XC7S75-1FGGA484C、XC7S15-1FTGB196C现场可编程门阵列芯片

【FPGA】Spartan®-7器件XC7S75-1FGGA484C、XC7S15-1FTGB196C现场可编程门阵列芯片

赛灵思 Spartan-7现场可编程门阵列采用运行频率超过200DMIP的MicroBlaze™软处理器&#xff0c;支持800Mb/s DDR3&#xff0c;基于28nm技术。FPGA是半导体器件&#xff0c;基于通过可编程互连系统连接的可配置逻辑块 (CLB) 矩阵。Spartan-7具有集成的模数转换器、专用安全特性以…
阅读更多...
回溯算法经典面试题

回溯算法经典面试题

⭐️前言⭐️ 本文汇总了常见的回溯算法题目&#xff0c;并将框架来进行运用&#xff0c;相信通过这篇文章&#xff0c;读者能够对回溯算法有一定了解。 &#x1f349;欢迎点赞 &#x1f44d; 收藏 ⭐留言评论 &#x1f4dd;私信必回哟&#x1f601; &#x1f349;博主将持续更…
阅读更多...
【MySQL入门指南】主键与唯一键的使用与区别

【MySQL入门指南】主键与唯一键的使用与区别

文章目录 一、主键1.基本语法2.使用案例 二、唯一键1.基本语法2.使用案例 一、主键 1.基本语法 -- 方式一 create table t5(id int primary key, ……); -- 设置id字段主键-- 方式二 create table t5(id int primary key,……primary key(id, ……); -- 每个表只能有一个主键…
阅读更多...
商城订单模块实战 - 分库分表实战及海量数据处理

商城订单模块实战 - 分库分表实战及海量数据处理

商城订单服务的实现 数据量 在设计系统&#xff0c;我们预估订单的数量每个月订单2000W&#xff0c;一年的订单数可达2.4亿。而每条订单的大小大致为1KB&#xff0c;按照我们在MySQL中学习到的知识&#xff0c;为了让B树的高度控制在一定范围&#xff0c;保证查询的性能&…
阅读更多...
归一化层（BatchNorm、LayerNorm、InstanceNorm、GroupNorm）

归一化层（BatchNorm、LayerNorm、InstanceNorm、GroupNorm）

参考博客 BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm、SwitchableNorm总结 PyTorch学习之归一化层&#xff08;BatchNorm、LayerNorm、InstanceNorm、GroupNorm&#xff09; BN&#xff0c;LN&#xff0c;IN&#xff0c;GN从学术化上解释差异&#xf…
阅读更多...
前端常见报错问题处理及技术点收集

前端常见报错问题处理及技术点收集

一、报错问题收集 1、页面停留半小时左右不动卡死报错问题 Uncaught (in promise) TypeError: Failed to fetch dynamically imported module: http://10.233.54.161/assets/index.f8110bbc.js Promise.then (async) E main.c19f562f.js:39 f main.c19f562f.js:39 z.onClick…
阅读更多...
Chatgpt聊天机器人系统开发

Chatgpt聊天机器人系统开发

智能聊天ChatGPT的主要功能包括&#xff1a; 对话生成&#xff1a;生成连贯、自然的对话回复&#xff0c;与用户进行自然而流畅的对话。 意图识别&#xff1a;识别用户的意图和需求&#xff0c;并提供相应的回复或建议。 语义理解&#xff1a;理解用户的语言表达&a…
阅读更多...
网络设备正常运行时间监控

网络设备正常运行时间监控

什么是正常运行时间监控 正常运行时间是衡量服务器或任何网络组件对其最终用户的可用性的指标。定期检查网络设备可用性的过程称为正常运行时间监控。正常运行时间监控有助于确保所有组件保持正常运行&#xff0c;而不会停机。 正常运行时间监控是关键的网络监控功能&#xf…
阅读更多...
Docker基础知识全解析

Docker基础知识全解析

​ Docker是一个开源的容器化平台&#xff0c;可以让开发者在容器中构建、打包、运行和发布应用程序&#xff0c;从而实现应用程序的快速部署和可移植性。Docker将应用程序和依赖项打包在一个轻量级的可移植容器中&#xff0c;这个容器可以在任何平台上运行&#xff0c;不会受到…
阅读更多...
Java 创建线程池的三种方式

Java 创建线程池的三种方式

一、 Java 创建线程池主要有以下三种方式 1. 默认线程池 ForkJoinPool 2. 通过调用执行器 Executors中的静态方法 3. 通过 ThreadPoolExector import java.util.concurrent.*;// 自定义线程工厂 class MyThreadFactory implements ThreadFactory {Override//ThreadFactory 主要…
阅读更多...
从零开始学习Linux运维，成为IT领域翘楚（一）

从零开始学习Linux运维，成为IT领域翘楚（一）

文章目录 &#x1f525;Linux概述&#x1f525;Linux下载安装&#x1f525;Linux三种网络配置&#x1f525;Linux 远程登录 &#x1f525;Linux概述 Linux内核最初只是由芬兰人林纳斯托瓦兹1991年在赫尔辛基大学上学时出于个人爱好而编写的。 Linux特点 首先Linux作为自由软件…
阅读更多...
递归实现指数型枚举

递归实现指数型枚举

77. 组合 方法&#xff1a;递归 class Solution { private:vector<vector<int>> res;vector<int> path;void solve(int n, int k, int idx) {if (path.size() k) {res.push_back(path);return ;}for (int i idx; i < n - (k-path.size()) 1; i) {pat…
阅读更多...
java 自定义Annotation注解

java 自定义Annotation注解

目录 1.声明注解 注解声明为interface&#xff08;注&#xff1a;这与interface接口没有任何关系&#xff09; 内部定义成员通常用value表示 使用 可以指定成员的默认值&#xff0c;使用default定义 介绍 2.JDK中的元注解 Retention&#xff1a; Target&#xff1a; …
阅读更多...
用于高负载多站点网络的 WordPress Multisite Cron

用于高负载多站点网络的 WordPress Multisite Cron

在易服客建站平台创建免费网站 500M免费空间&#xff0c;可升级为10GB电子商务网站 创建免费网站 用于高负载多站点网络的 WordPress Multisite Cron 发布于 2023年3月18日 你也许知道WordPress 内置 CRON 的工作方式与传统 CRON 不同。 它不是在指定时间触发&#xff0c…
阅读更多...
辨析 变更请求、批准的变更请求、实施批准的变更请求

辨析 变更请求、批准的变更请求、实施批准的变更请求

变更请求、批准的变更请求、实施批准的变更请求辨析 辨析各种变更请求&#xff0c;不服来辨。 变更请求 定义&#xff1a;对正规受控的文件或计划(范围、进度、成本、政策、过程、计划或程序)等的变更&#xff0c;以反映修改或增加的意见或内容 根据变更请求的工作内容可将变…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023