⭐️前言⭐️
本文汇总了常见的回溯算法题目,并将框架来进行运用,相信通过这篇文章,读者能够对回溯算法有一定了解。
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁
🍉博主将持续更新学习记录收获,友友们有任何问题可以在评论区留言
🍉博客中涉及源码及博主日常练习代码均已上传GitHub

📍内容导读📍
- 🍅1.回溯算法框架
- 🍅2.经典题目练习
- 2.1 全排列问题
- 2.2 N皇后问题
🍅1.回溯算法框架
解决一个回溯问题,实际上就是一个决策树的遍历过程,站在回溯树的一个节点上,你只需要考虑3个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
接下来通过全排列与N皇后的经典回溯问题来应用理解这个框架。
代码框架如下:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
核心是for循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」。
🍅2.经典题目练习
2.1 全排列问题
https://leetcode.cn/problems/permutations/
n个不重复的数,全排列共有n!个。
下图中[3]就是路径,记录你已经做过的选择;[1,2]就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层叶子节点,这里也就是选择列表为空的时候。
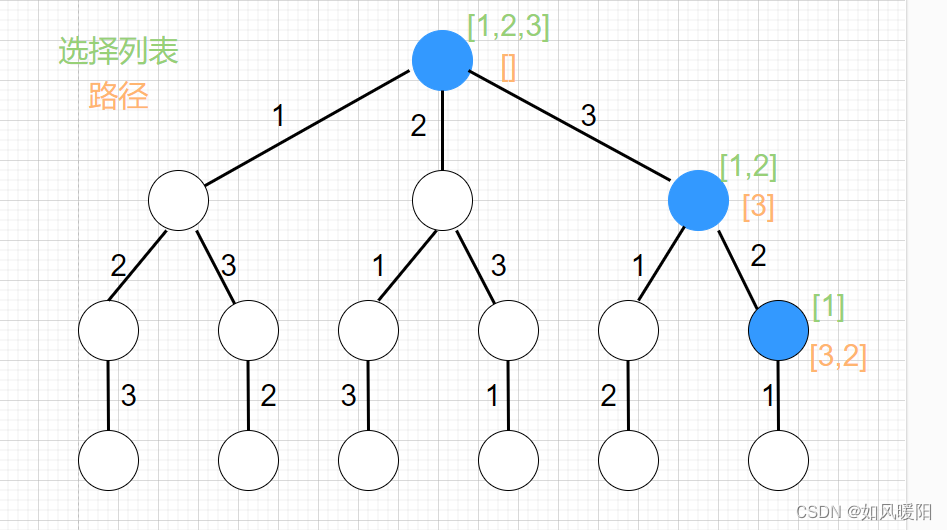
我们定义的backtrack函数就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的叶子节点,其路径就是一个全排列。
代码实现:
class Solution {
List<List<Integer>> res=new LinkedList<>();
// 主函数,输入一组不重复的数字,返回他们的全排列。
public List<List<Integer>> permute(int[] nums) {
//记录路径
LinkedList<Integer> track=new LinkedList<>();
//路径中的元素会被标记为true,避免重复使用
boolean[] used=new boolean[nums.length];
backtrack(nums,track,used);
return res;
}
// 路径记录在track中
// 选择列表:nums中不存在于track的那些元素
// 结束条件:nums中的元素全都在track中出现
void backtrack(int[] nums,LinkedList<Integer> track,boolean[] used) {
//触发结束条件
if(track.size()==nums.length) {
res.add(new LinkedList(track));
return;
}
for(int i=0;i<nums.length;i++) {
// 排除不合法的选择
if(used[i]) continue;
// 做选择
track.add(nums[i]);
used[i]=true;
backtrack(nums,track,used);
// 取消选择
used[i]=false;
track.removeLast();
}
}
}
https://leetcode.cn/problems/permutations-ii/description/
注意:
该题目与上题相比,存在了重复的元素,所以在保存结果的时候,不需要保存数字结果相同的结果,那么这个时候就需要我们剪枝,比如[1,2,2 '] 路径记录下来以后,路径[1,2 ',2]就不会被记录。
如果涉及考虑重复元素,或者大小比较的情况,首先应该对列表进行排序,然后再去进一步记录结果。
那么针对重复元素造成结果相同的这部分剪枝的条件为:和前一个元素值相同(此处隐含这个元素的index>0),并且前一个元素还没有被使用过。
比如[1,2,2 '] 路径记录下来以后,路径[1,2 ‘,2]首先记录2’,在数组中的排序为1,2,2’,因为2’与数组中前一个数值相同,并且没被用过,所以该路径直接被剪枝。
即代码:
if(i>0&&nums[i-1]==nums[i]&&!used[i-1]) continue;
总代码实现:
class Solution {
List<List<Integer>> res=new LinkedList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
LinkedList<Integer> track=new LinkedList<>();
boolean[] used=new boolean[nums.length];
Arrays.sort(nums);
backtrack(nums,track,used);
return res;
}
void backtrack(int[] nums,LinkedList<Integer> track,boolean[] used) {
if(track.size()==nums.length) {
res.add(new LinkedList(track));
return;
}
for(int i=0;i<nums.length;i++) {
if(used[i]) continue;
if(i>0&&nums[i-1]==nums[i]&&!used[i-1]) continue;
track.add(nums[i]);
used[i]=true;
backtrack(nums,track,used);
used[i]=false;
track.removeLast();
}
}
}
2.2 N皇后问题

题解思路:
该题其实也和上边的全排列相似,也是回溯问题,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
剪枝的条件是:
判断是否符合规则,该位置的上方、左上方和右上方是否有皇后。
代码实现:
class Solution {
List<List<String>> res = new ArrayList<>();
/* 输入棋盘边长 n,返回所有合法的放置 */
public List<List<String>> solveNQueens(int n) {
// '.' 表示空,'Q' 表示皇后,初始化空棋盘
List<String> board = new ArrayList<>();
for (int i = 0; i < n; i++) {
StringBuilder sb = new StringBuilder();
for (int j = 0; j < n; j++) {
sb.append('.');
}
board.add(sb.toString());
}
backtrack(board, 0);
return res;
}
// 路径:board 中小于 row 的那些行都已经成功放置了皇后
// 选择列表:第 row 行的所有列都是放置皇后的选择
// 结束条件:row 超过 board 的最后一行
void backtrack(List<String> board, int row) {
// 触发结束条件
if (row == board.size()) {
res.add(new ArrayList<>(board));
return;
}
int n = board.get(row).length();
for (int col = 0; col < n; col++) {
// 排除不合法选择
if (!isValid(board, row, col)) {
continue;
}
// 做选择
StringBuilder sb = new StringBuilder(board.get(row));
sb.setCharAt(col, 'Q');
board.set(row, sb.toString());
// 进入下一行决策
backtrack(board, row + 1);
// 撤销选择
sb.setCharAt(col, '.');
board.set(row, sb.toString());
}
}
/* 是否可以在 board[row][col] 放置皇后? */
boolean isValid(List<String> board, int row, int col) {
int n = board.size();
/* 检查上方是否有皇后互相冲突 */
for(int i=0;i<row;i++) {
if(board.get(i).charAt(col)=='Q') return false;
}
/* 检查右上方是否有皇后互相冲突 */
for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++) {
if(board.get(i).charAt(j)=='Q') return false;
}
/* 检查左上方是否有皇后互相冲突 */
for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--) {
if(board.get(i).charAt(j)=='Q') return false;
}
return true;
}
}
该题目即在上边题目的代码上做出简单变动即可ac,就是不用在记录路径了,定义变量res记录符合规则的情况数,如果row到达底层,就让res++,最后返回res即可。
代码实现:
class Solution {
int res=0;
public int totalNQueens(int n) {
List<String> board=new ArrayList<>();
for(int i=0;i<n;i++) {
StringBuffer sb=new StringBuffer();
for(int j=0;j<n;j++) {
sb.append(".");
}
board.add(sb.toString());
}
backtrack(board,0);
return res;
}
void backtrack(List<String> board,int row) {
if(row==board.size()) {
res++;
return;
}
int n=board.get(row).length();
for(int col=0;col<n;col++) {
if(!isValid(board,row,col)) continue;
StringBuffer sb=new StringBuffer(board.get(row));
sb.setCharAt(col,'Q');
board.set(row,sb.toString());
backtrack(board,row+1);
sb.setCharAt(col,'.');
board.set(row,sb.toString());
}
}
boolean isValid(List<String> board,int row,int col) {
int n=board.size();
for(int i=0;i<row;i++) {
if(board.get(i).charAt(col)=='Q') return false;
}
for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++) {
if(board.get(i).charAt(j)=='Q') return false;
}
for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--) {
if(board.get(i).charAt(j)=='Q') return false;
}
return true;
}
}
⭐️最后的话⭐️
总结不易,希望uu们不要吝啬你们的👍哟(^U^)ノ~YO!!如有问题,欢迎评论区批评指正😁