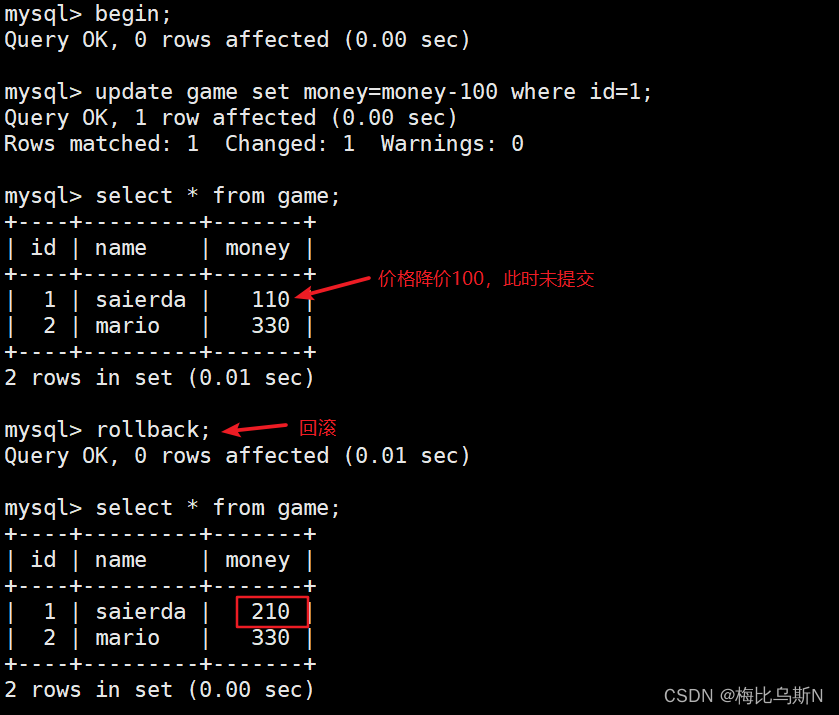
两台相机基线距离约1200mm，对20m外的一个LED发光点进行持续观测，效果如下视频所示：

可见$Z$方向的重复性精度比较差，波动量甚至多于2mm了，而以10mm导轨基准距离为基准，精度测试结果也比较差，如下图所示：

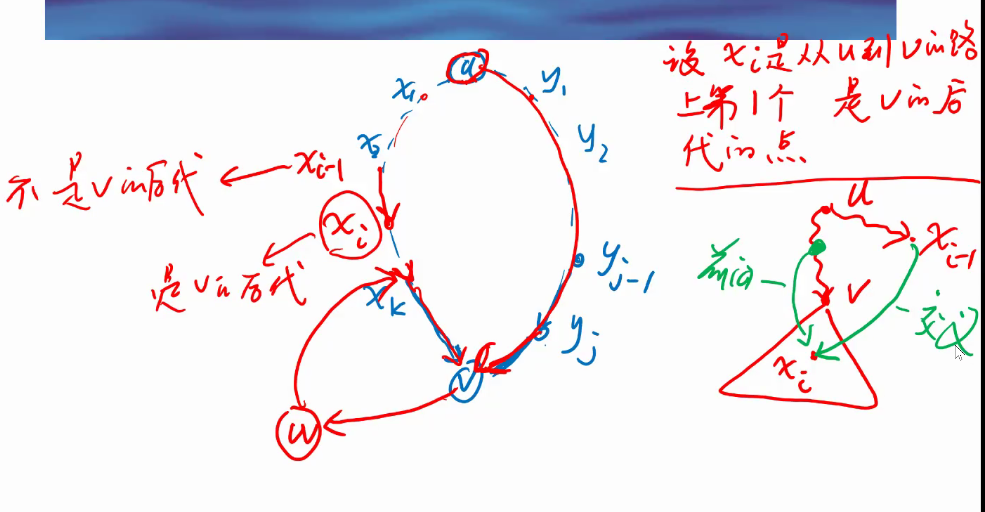
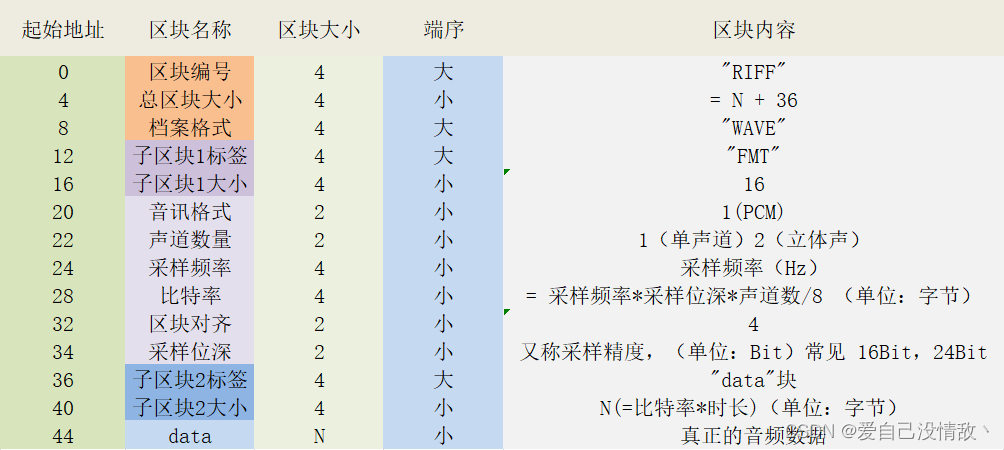
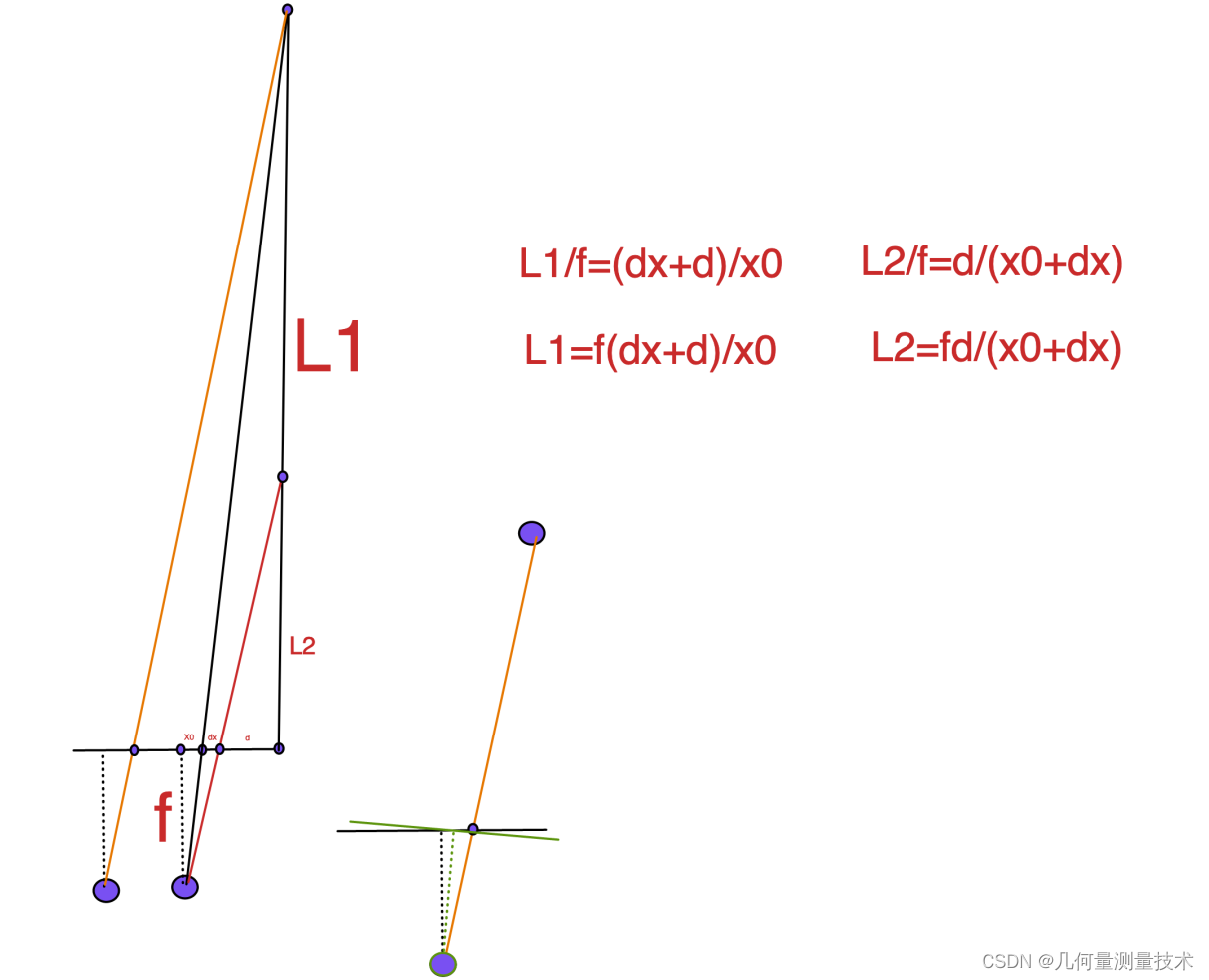
现对这种情况进行分析。双目视觉测量过程中，在进行完立体矫正后，左侧相机的成像模型可简化为遵循如下图所示的几何关系：

其中，$f$表示焦距，$x_0$表示物点在左相机像面距离主点在$u$方向的距离值，$d_x$表示由于像点质心提取的误差，$d$代表像点距离基线中点的距离，$L_1$表示物点距离基线中点之间的距离，$L_2$表示像点产生$d_x$误差对应的虚拟物点相对于基线中点之间的距离。根据简单的相似三角形原理，有如下公式成立：

$$\frac{L_1}{f}=\frac{d_x+d}{x_0}$$，
$$\frac{L_2}{f}=\frac{d}{x_0+d_x}$$
根据这两个公式，可知由于像面$u$方向坐标分量发生变化引起的纵深方向误差为$L_1-L_2$，则将上述两个公式带入$L_1-L_2$，可以得到如下等式：
$$L_1-L_2=f\frac{d_x+d}{x_0}-f\frac{d}{x_0+d_x}$$
整理得：
$$L_1-L_2=\frac{f{d}_x}{x_0}+fd(\frac{1}{x_0}-\frac{1}{x_0+d_x})$$
从这个师资可以看出来，如果想让纵深方向的误差
$L_1-L_2$尽可能小，需要保证$x_0$尽可能大，也就是左相机光斑位置在水平方向尽可能距离图像中心远一些，让$d_x$尽可能小，也就是质心识别精度尽可能高。但是这个模型中$d、x_0、f$三者之间存在着一定的耦合关系。对这个问题进行仿真，代码如下：

import numpy as np
import cv2
import math

# 左相机内参矩阵
mtx_l = np.array([[10015.2812383159, 0.00000000e+00, 659.197479841463, 0],
                  [0.00000000e+00, 10014.0958495599, 470.925014875954, 0],
                  [0.00000000e+00, 0.00000000e+00, 1.00000000e+00, 0]])

# 右相机内参矩阵
mtx_r = np.array([[10051.5363357765, 0.00000000e+00, 697.234956187232, 0],
                  [0.00000000e+00, 10050.409518322, 424.52423603342, 0],
                  [0.00000000e+00, 0.00000000e+00, 1.00000000e+00, 0]])

# 两个相机之间的旋转矩阵R_lr和平移矩阵T_lr
R_lr = np.array([[0.999943847448837, 0.008365705276491, 0.006505145997198],
                 [-0.008395292001614, 0.999954478671489, 0.004534275800987],
                 [-0.006466917459317, -0.004588633789993, 0.999968561215059]])
T_lr = np.array([[-896.678233796519],
                 [-23.2722512628781],
                 [39.3967835788876]])

# 通过相机内参计算实际的左相机焦距
f_l = mtx_l[0][0] * 0.0053

# 设置光斑质心u方向的偏移量，质心偏移量的单位是像素，进行相似三角形比例计算时需要将单位转换为mm。
d_x = 0.1 * 0.0053

# 输入左相机采集到的光斑质心坐标
l0 = np.array([1050.5, 751.134])

# 计算x_0，为质心坐标的u与相机内参中u_0的差值：(u-u_0)，将单位统一为mm。
x_0 = (l0[0] - mtx_l[0][2]) * 0.0053

# 计算d，在模型中为基线长度D的1/2减去x_0和像素坐标偏移量：(D/2-x_0-d_x)，计算时需要将单位统一为mm。
d = math.sqrt(T_lr[0] * T_lr[0] + T_lr[1] * T_lr[1] + T_lr[2] * T_lr[2]) / 2 - x_0 - d_x

# 根据针孔相机成像模型和相似三角形公式推导，计算不同像素偏移量u对空间点三维坐标的解算影响，用解算增加质心偏移量前后三维点坐标之间的距离z表示。
z = (f_l * d_x) / x_0 + f_l * d * (1 / x_0 - 1 / (x_0 + d_x))
print(z)

和实测实验数据进行联合半物理仿真，数据如下图所示：

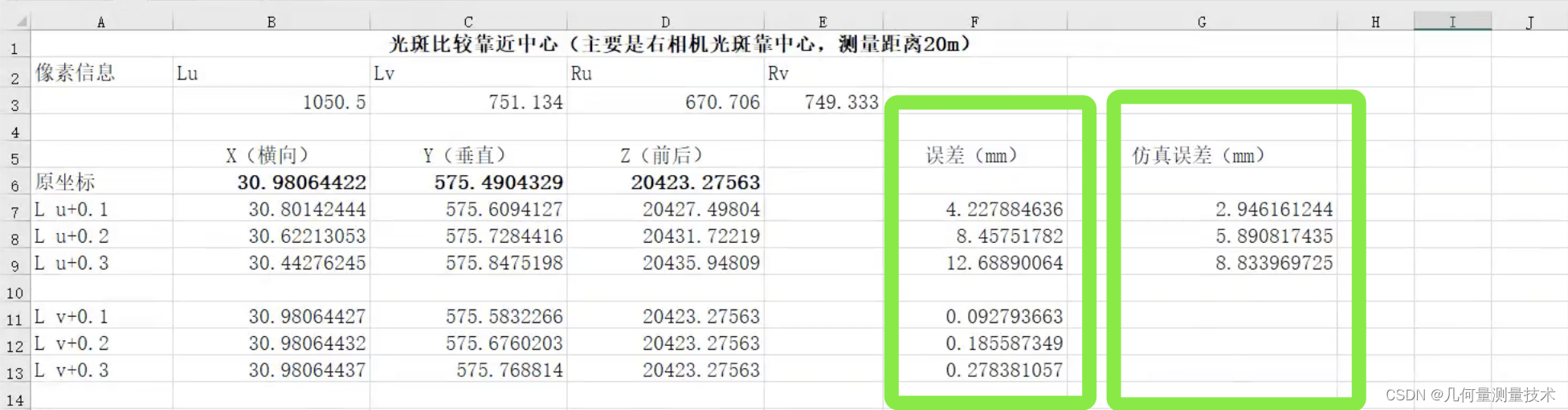
可以看出仿真误差和实际误差累积趋势相同，实际误差大于仿真误差，证明了：远距离双目视觉测量系统中，如果被测目标的质心在水平$u$方向存在0.1像素的误差，目标点纵深方向的坐标会波动约2mm。所以可以得到如下两点结论：

• 双目视觉测量系统不适合执行远距离测量任务；
• 水平方向的质心提取误差会引起被观测点空间三维坐标纵深方向分量较大的不确定度。

实测场景如下图所示：