1. 单连通图的判断算法：
   （1）对每个点进行dfs得到一棵dfs树；
   （2）判断是否存在前向边和横向边，若有则必定存在两个点之间有至少2条简单路径，因此该图不属于单连通图；
   （3）若对所有dfs树不存在（2）中情况，则该图是单连通图。
2. 算法时间复杂度：对$V$个点进行dfs，每次dfs的时间为$O(V+E)$，因此总时间复杂度为$O(V\ast (V+E))$.
3. 算法正确性证明：
   必要性(对于单连通图，每个点出发的dfs树中不存在前向边和横向边)：假设点A，B之间存在前向边AB，根据前向边的定义，应存在另外一条由树边组成的路径A->B，不满足至多1条简单路径的要求；
   假设点A，B之间存在横向边AB，根据算法步骤易知A，B应在以某个点为根的dfs树中，设为R，那么在点R，B之间至少存在R->A->B和R->B两条路径，不满足至多1条简单路径的要求；
   充分性（对于一个图，每个点出发的dfs树中不存在前向边或横向边则是单连通图）:等价于证明逆否命题，若图中A，B两个点之间存在2条路径，则一定对应存在的前向边或者横向边。设A，B之间存在路径$(A,x_1,x_2,...,x_n,B)$以及$(A,y_1,y_2,...,y_m,B)$,
   当$m,n$均大于0时，根据白色路径定理，$x_i$，$y_j$以及B均为A的子孙，因此$(x_n,B)$和$(y_m,B)$必有一个是横向边；（此处有纰漏）
   当$m=0,n>0$时，$(A,B)$是前向边或者$(x_n,B)$是横向边；当$m>0,n=0$时类同。
   以上。

---

以下是老师ppt上的证明：
大题思路相同，但我证明最后“因此$(x_n,B)$和$(y_m,B)$必有一个是横向边”的论断是错的，可以修补。

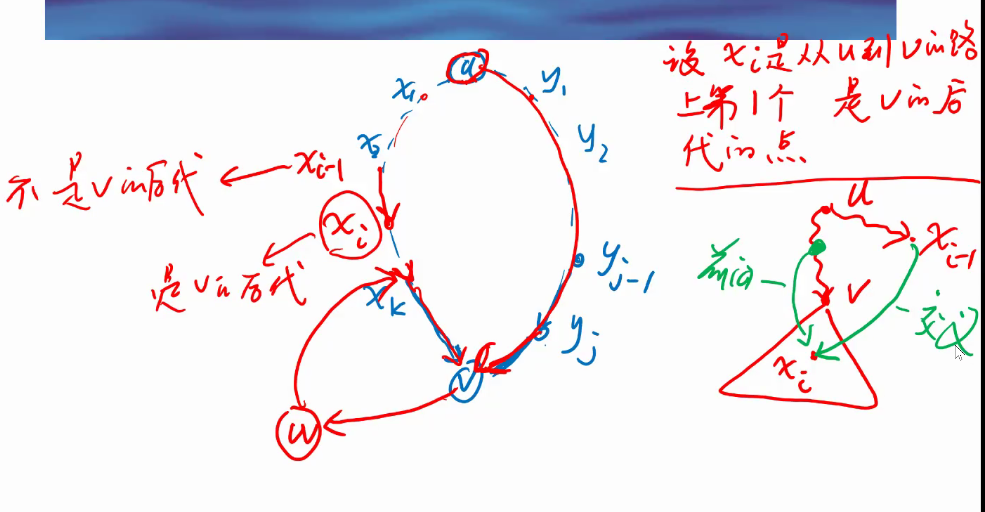
分为两条路径上不存在v的后代和存在v的后代两种情况。第一种可以断定$(x_r,v)$和$(y_t,v)$中有一条是前向边或交叉边；第二种，存在这样一条搜索路径$u\to y_j\to v\to w\to x_k\to v$（如下图所示，标号对应关系：$j=t$，$k=r$），此时$(y_k,v)$是树边，而$(x_j,v)$是返回边，但我们仍可以找到这样的两条边$(x_{i-1},x_i)$和$(y_{i-1},y_i)$其中有一条是前向边或交叉边。