1、完全二叉树的权值

1）题目

给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 A1, A2, ··· AN，如下图所示：

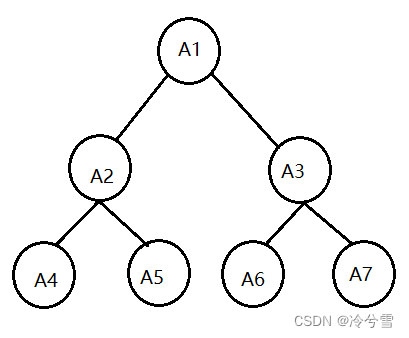
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 1。

输入格式:

第一行包含一个整数 N（1≤N≤10^5）。

第二行包含 N 个整数 A1, A2, ··· AN （−10^5 <= Ai<=10^5）。

输出格式:

输出一个整数代表答案。

输入样例:

在这里给出一组输入。例如：
7
1 6 5 4 3 2 1
输出样例:

在这里给出相应的输出。例如：
2

2)题目解析

题目要求我们输入n个数字，这n个数字是一颗树的层序遍历，并且这是一颗完全二叉树。计算哪一层数字之和最大，并输出该层数。注：根的深度是 1。

3）代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        long []arr= new long[n];
        for (int j=0;j<n;j++){
            arr[j]=sc.nextInt();
        }
//第一层只有一个节点，p表示该层的节点数
        int p=1;
//max表示当前 最大权值之和
        long max = 0;
//l表示max所在的层数，l1是跟着循环遍历的层数
        int l=1,l1=1;
//i表示节点总数3，不超过n
        int i=0;
        while (i<n){
            int j=p;
//max1表示当前层的权值之和
            long max1=0;
//j=p，表示该层的节点数
            while (j!=0){
                max1+=arr[i++];
                j--;
                if (i==n)
                    break;
            }
//判断当前层是否是最大权值之和
            if (max<max1) {
                max =  max1;
                l=l1;
            }
//下一层的节点数=p*2，深度=l1+1
            p*=2;
            l1++;
        }
        System.out.println(l);
    }
}

2、小字辈

1）题目

本题给定一个庞大家族的家谱，要请你给出最小一辈的名单。

输入格式：

输入在第一行给出家族人口总数 N（不超过 100 000 的正整数） —— 简单起见，我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号，其中第 i 个编号对应第 i 位成员的父/母。家谱中辈分最高的老祖宗对应的父/母编号为 -1。一行中的数字间以空格分隔。

输出格式：

首先输出最小的辈分（老祖宗的辈分为 1，以下逐级递增）。然后在第二行按递增顺序输出辈分最小的成员的编号。编号间以一个空格分隔，行首尾不得有多余空格。

输入样例：
9
2 6 5 5 -1 5 6 4 7
输出样例：
4
1 9

2）题目解析

题目要求我们输入N个数，这N个数表示从1到N的其父节点编号，家谱中辈分最高的老祖宗对应的父/母编号为 -1，然后找出其最小辈的编号。输入样例对应图如下图，可以帮助你们更好理解。

3）代码

import java.util.*;

public class Main1 {
    //L表示当前递归到的最大层数
    static int L;
    //使用队列来存储结果，先进先出
    static Queue<Integer> queue=new LinkedList<>();
    //递归函数
    static void sonTree(int []arr,int father,int l){
        for (int i=1;i<arr.length;i++){
            //如果arr[i]=father，表示编号为i的父亲是father，再进入递归函数，
            //寻找以i为父亲的子节点
            if (arr[i]==father){
                sonTree(arr,i,l+1);
            }
        }
        //如果当前递归的l小于L（当前递归到的最大层数），直接return，肯定不是最小辈
        if (l<L)
            return;
        if (l>L){
        //如果当前递归的l大于L（当前递归到的最大层数），即是新的最大递归层数，
        // 清空队列，重新添加元素    
            L=l;
            queue.clear();
        }
        queue.add(father);
    }
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        int []arr=new int[n+1];
        int x=0; //x表示-1祖宗的编号
        for (int i=1;i<=n;i++){
            arr[i]=sc.nextInt();
            //记录祖宗的编号
            if (arr[i]==-1)
                x=i;
        }
        //从1楼开始
        int l=1;
        sonTree(arr,x,l);
        System.out.println(L);
        while (queue.size()!=1){
            System.out.print(queue.poll()+" ");
        }
        System.out.print(queue.poll());
    }
}

上述代码是递归方法，但是因为题目数据量过大，N（不超过 100 000 的正整数），因此部分题给用例会超时或者其他错误，欢迎大佬在评论区给出建议。下面是正确的另一种方法：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
  public static void main(String[] args) throws IOException {
        //因为题目数据用量特别大，所以用BufferedReader，提高数据读取时间
        BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
        int n=Integer.parseInt(bf.readLine());
        //因为所给数据是每个人的父母，所以用arr[]来存放第i人的子女
        ArrayList<Integer> arr[]=new ArrayList[n+1];
        for (int i=0;i<n+1;i++){
        //先要给每个arr[]分配内存，不然都是null
            arr[i]=new ArrayList<>();
        }
        int[] count=new int[n+1];//存放每个人的辈分
        Queue<Integer> q=new LinkedList<>();//层序遍历来求辈分
        //如果只有一个人直接输出
        if (n==1){
            System.out.println(1);
            System.out.print(1);
            return;
        }
        //读取n个数据
        String s=bf.readLine();
        String[] ss=s.split(" ");
        int x=0;
        int lzz=0;//记录老祖宗的编号
        for (int i=1;i<=n;i++){
            x= Integer.parseInt(ss[i-1]);
            //记录祖宗的编号
            if (x==-1)
                 lzz=i;
            else//将i加入到该第x个ArrayList集合中，表示第i个人是第x个人的子女，
                arr[x].add(i);
        }
        //先将老祖宗入队
        q.add(lzz);
        int L=1;//表示辈分
        count[lzz]=1;//老祖宗的辈分是1
       while (!q.isEmpty()){
            int t=q.peek();
            q.poll();
            for (int i=0;i<arr[t].size();i++){
                count[arr[t].get(i)]=count[t]+1;//更新每个子女的辈分
                //更新新的最小辈分的值
                L=Math.max(L,count[arr[t].get(i)]);
                //把子女入队
                q.add(arr[t].get(i));
            }
        }
        System.out.println(L);
        boolean b=true;
        //输出
        for (int i=1;i<=n;i++){
            if (count[i]==L){
                if (b){
                    System.out.println(i);
                    b=false;
                }else
                    System.out.println(" "+i);
            }
        }
    }
}

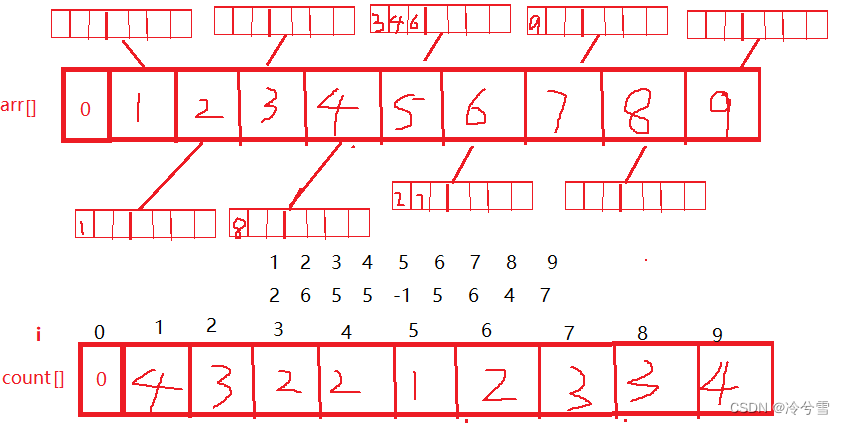
为了更好理解可以看看下面图，先找到5的子女并放入arr[x]中。子女的辈分值为二，然后在count[]的相应位置存储其辈分值。然后再找3，4，6的子女并放入3，4，6对应的arr[]中，其对应的子女的辈分值为3·· ···

L为最大的辈分值，即是最小辈分，然后去count[]数组中找与L相等的辈分值，并输出其对应的i值。

3、根据后序和中序遍历输出先序遍历

1）题目

本题要求根据给定的一棵二叉树的后序遍历和中序遍历结果，输出该树的先序遍历结果。

输入格式:

第一行给出正整数N(≤30)，是树中结点的个数。随后两行，每行给出N个整数，分别对应后序遍历和中序遍历结果，数字间以空格分隔。题目保证输入正确对应一棵二叉树。

输出格式:

在一行中输出Preorder: 以及该树的先序遍历结果。数字间有1个空格，行末不得有多余空格。

输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
Preorder: 4 1 3 2 6 5 7

2）题目解析

题目给定我们N个数，然后在下两行分别给出由这N个数组成的一颗二叉树的后序遍历和中序遍历。然后要求我们输出前序遍历。我们应该先根据后序遍历和中序遍历，构建出这颗二叉树，然后再进行前序遍历并输出。

3）代码

import java.util.*;

public class Main {
    public static class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int val) {
        this.val = val;
    }
}
    public static void main(String[] args) {
    Scanner sc=new Scanner(System.in);
    int n=sc.nextInt();
    int []hx=new int[n];
    int []qx=new int[n];
    for (int i=0;i<n;i++){
        hx[i]=sc.nextInt();
    }
    for (int i=0;i<n;i++){
        qx[i]=sc.nextInt();
    }
    TreeNode tree=buildTree(qx,hx);

    //使用List集合存储该树的前序遍历，方便输出
    List<Integer> list=new ArrayList<>();
    preorder(tree,list);
    int j=0;
    System.out.print("Preorder: ");
    while (j!=list.size()-1){
        System.out.print(list.get(j)+" ");
        j++;
    }
        System.out.print(list.get(j));
}
     //前序遍历，使用List 集合存储
     public static void preorder(TreeNode root, List<Integer>list){
         if (root == null) {
             return;
         }
         list.add(root.val);
         preorder(root.left, list);
         preorder(root.right, list);
     }
    //前序遍历
     public static void preOrder(TreeNode head) {
         if (head == null) {
             return;
         }
         System.out.print(head.val + " ");
         preOrder(head.left);
         preOrder(head.right);
     }

    static int index = 0;
    //构建二叉树
    public static TreeNode buildTree(int[] inorder, int[] postorder) {
        index = postorder.length-1;
        return buildTree(postorder, inorder, 0, inorder.length);
    }
    // index不断在后序遍历中找根节点，每次找完之后，根据找到的根节点将中序遍历分成
    //左右两部分，左侧为根的左子树，右侧为根的右子树
    // 注意：与前序中序还原二叉树不同的是，此次需要先还原右子树
    private static TreeNode buildTree(int[] postorder, int[] inorder, int left,
 int right){
        //如果left>=right，即左右节点遍历到同一节点，这时就要停止递归
        if(left >= right){
            return null;
        }
        // 创建根节点
        TreeNode root = new TreeNode(postorder[index]);
        // 在中序遍历结果中找到根的位置
        int rootIdx = left;
        //寻找根位置
        while(rootIdx < right){
            if(inorder[rootIdx] == postorder[index])
                break;
            rootIdx++;
        }
        index--;
        //要先构建右子树，再构建左子树，这是由后序遍历决定的
        //[rootIdx+1, right): 右子树中的所有节点的范围
        // 递归创建根的右子树
        root.right = buildTree(postorder, inorder, rootIdx+1, right);
        //[left, rootIdx)：左子树中的所有节点的范围
        // 递归创建根的左子树
        root.left = buildTree(postorder, inorder, left, rootIdx);
        return root;
    }
}