一、问题描述

地下水系统是一个复杂的非线性、随机系统。建立微分方程模型需要大量详尽的地下水文地质资料。这些实测数据往往很难获得。径向基函数网络训练速度快，具有很强的非线性映射能力，能够实现较高精度的地下水位预测。
由于预测的值是地下水的水位，因此输出的结果是一个标量，故输出层的神经元节点个数为1 。
采用了影响水位深度的5个因素作为自变量，分别为河道流量、气温、饱和差、降水量与蒸发量，形成函数关系：
$y=f\left(x_1,x_2,x_3,x_4,x_5\right)$

二、RBF径向基网络实现地下水位预测

MATLAB自带的神经网络工具箱提供了newrb函数，可以创建一个径向基神经网络。
在newrb函数创建的径向基网络中，隐含层的节点个数是不确定的。函数根据用户设置的误差目标，向网络中不断添加新的隐含层节点，并调整节点中心、标准差及权值，直到所得到的网络达到预期的误差要求。
本文使用newrb函数完成地下水水位的预测。
算法流程图如下：

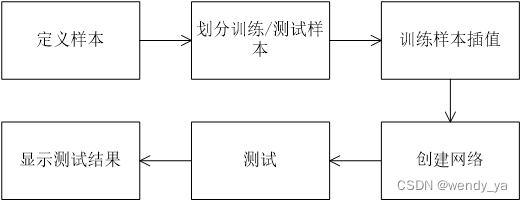
三、算法步骤

3.1 定义数据样本

实验选择的是滦河某观测站24个月的地下数位实测序列值和5个影响因子的实测值，5个影响因子分别是：气温、饱和差、降水量、蒸发量和水位。
输入向量定义为524的矩阵，目标输出值为124行向量 ：

% 输入
x = [ 1.5, 1.8, 4.0, 13.0, 5.0, 9.0, 10.0, 9.0, 7.0, 9.5, 5.5, 12.0,...
    1.5, 3.0, 7.0, 19.0, 4.5, 8.0, 57.0, 35.0, 39.0, 23.0, 11.0, 4.5;
     -10.0, -10.0, -2.0, 10.0, 17.0, 22.0, 23.0, 21.0, 15.0, 8.5, 0, -8.5,...
     -11.0, -7.0, 0, 10.0, 18.0, 21.5, 22.0, 19.0, 13.0, 6.0, 1.0, -2.0;
     1.2, 2.0, 2.5, 5.0, 9.0, 10.0, 8.0, 6.0, 5.0, 5.0, 6.2, 4.5,...
     2.0, 2.5, 3.0, 7.0, 10.0, 11.0, 5.5, 5.0, 5.0, 3.0, 2.0, 1.0;
     1.0, 1.0, 6.0, 30.0, 18.0, 13.0, 29.0, 74.0, 21.0, 15.0, 14.0, 11.0,...
     1.0, 2.0, 4.0, 0, 19.0, 81.0, 186.0, 114.0, 60.0, 35.0, 4.0, 6.0;
     1.2, 0.8, 2.4, 4.4, 6.3, 6.6, 5.6, 4.6, 2.3, 3.5, 2.4, 0.8,...
     1.3, 1.3, 4.1, 3.2, 6.5, 7.7, 5.5, 4.6, 3.6, 2.6, 1.7, 1.0
    ];

y = [6.92, 6.97, 6.84, 6.5, 5.75, 5.54, 5.63, 5.62, 5.96, 6.3, 6.8, 6.9,...
    6.7, 6.77, 6.67, 6.33, 5.82, 5.58, 5.48, 5.38, 5.51, 5.84, 6.32, 6.56];

3.2 划分训练数据与测试数据

使用第6号至第24号样本训练得出模型，再对第1号至第5号样本进行检验：

% 训练输入向量
trainx = x(:, 6:24);
% 训练样本对应的输出
trainy = y(6:24);

% 测试输入向量
testx = x(:,1:5);
% 测试样本对应的输出
testy = y(1:5);

3.3 数据增强

为充分利用训练样本，对19份训练样本进行二维插值，将样本数量增加到100份：

% 训练样本的个数
N = size(trainx, 2);
X = [trainx; trainy];

% 网格
[xx0, yy0] = meshgrid(1:N, 1:6);
[xx1,yy1] = meshgrid(linspace(1,N,100), 1:6);

% 使用interp2函数做二维三次插值
XX = interp2(xx0, yy0, X, xx1, yy1, 'cubic');

% 形状复原
trainx = XX(1:5, :);
trainy = XX(6, :);

3.4 创建径向基神经网络

使用newrb函数创建径向基神经网络。径向基网络需要若干参数，在这里设置误差容限为1e-8，扩散因子为22，最大神经元个数为101：

% 误差容限
er = 1e-8;

% 扩散因子
spread = 22;

% 神经元个数
N = 101;
net = newrb(trainx, trainy, er, spread, N);

3.5 测试

使用创建完成的径向基网络模型对第1-5份样本进行测试：

yy = net(testx);

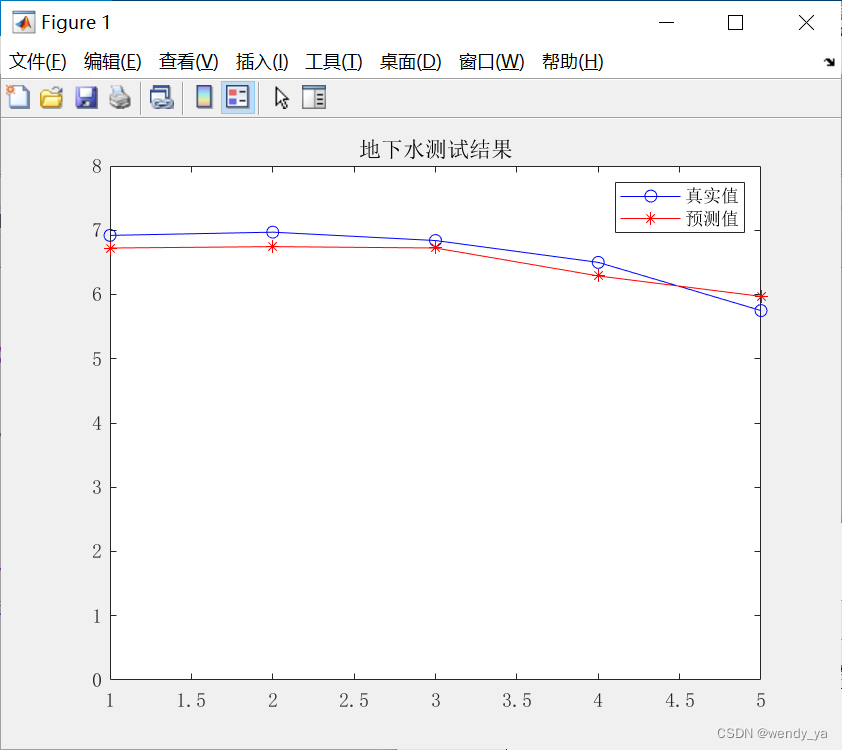
四、结果展示

真实值与测试值对比如下：

五、完整代码

完整代码如下：

% rbf_underwater.m
%% 清理工作空间
clear,clc
close all

%% 定义输入数据
% 输入
x = [ 1.5, 1.8, 4.0, 13.0, 5.0, 9.0, 10.0, 9.0, 7.0, 9.5, 5.5, 12.0,...
    1.5, 3.0, 7.0, 19.0, 4.5, 8.0, 57.0, 35.0, 39.0, 23.0, 11.0, 4.5;
     -10.0, -10.0, -2.0, 10.0, 17.0, 22.0, 23.0, 21.0, 15.0, 8.5, 0, -8.5,...
     -11.0, -7.0, 0, 10.0, 18.0, 21.5, 22.0, 19.0, 13.0, 6.0, 1.0, -2.0;
     1.2, 2.0, 2.5, 5.0, 9.0, 10.0, 8.0, 6.0, 5.0, 5.0, 6.2, 4.5,...
     2.0, 2.5, 3.0, 7.0, 10.0, 11.0, 5.5, 5.0, 5.0, 3.0, 2.0, 1.0;
     1.0, 1.0, 6.0, 30.0, 18.0, 13.0, 29.0, 74.0, 21.0, 15.0, 14.0, 11.0,...
     1.0, 2.0, 4.0, 0, 19.0, 81.0, 186.0, 114.0, 60.0, 35.0, 4.0, 6.0;
     1.2, 0.8, 2.4, 4.4, 6.3, 6.6, 5.6, 4.6, 2.3, 3.5, 2.4, 0.8,...
     1.3, 1.3, 4.1, 3.2, 6.5, 7.7, 5.5, 4.6, 3.6, 2.6, 1.7, 1.0
    ];

y = [6.92, 6.97, 6.84, 6.5, 5.75, 5.54, 5.63, 5.62, 5.96, 6.3, 6.8, 6.9,...
    6.7, 6.77, 6.67, 6.33, 5.82, 5.58, 5.48, 5.38, 5.51, 5.84, 6.32, 6.56];

%% 划分训练数据与测试数据

% 训练输入向量
trainx = x(:, 6:24);
% 训练样本对应的输出
trainy = y(6:24);

% 测试输入向量
testx = x(:,1:5);
% 测试样本对应的输出
testy = y(1:5);

%% 对训练样本做插值

% 训练样本的个数
N = size(trainx, 2);
X = [trainx; trainy];

% 网格
[xx0, yy0] = meshgrid(1:N, 1:6);
[xx1,yy1] = meshgrid(linspace(1,N,100), 1:6);

% 使用interp2函数做二维三次插值
XX = interp2(xx0, yy0, X, xx1, yy1, 'cubic');

% 形状复原
trainx = XX(1:5, :);
trainy = XX(6, :);

%% 创建网络
% 误差容限
er = 1e-8;

% 扩散因子
spread = 22;

% 神经元个数
N = 101;
net = newrb(trainx, trainy, er, spread, N);

%% 测试 
yy = net(testx);

%% 计算、显示相对误差
e = (testy - yy)./testy;
fprintf('相对误差: \n ');
fprintf('%f   ', e);
fprintf('\n\n');
% 平均相对误差
m = mean( abs(e) );
fprintf('平均相对误差: \n %f\n', m);

% 最大相对误差
ma = max(abs(e));
fprintf('最大相对误差: \n %f\n', ma);

% 显示实际值与拟合值
figure(1)
plot(1:5, testy, 'bo-')
hold on
plot(1:5, yy, 'r*-')
title('地下水测试结果')
legend('真实值', '预测值')
axis([1,5,0,8])

% 显示残差
figure(2)
plot(1:5, abs(testy - yy), '-o')
title('残差')
axis([1,5,0,0.3])

---

ok，以上便是本文的全部内容了，制作不易，如果对你有所帮助，记得点个赞哟~