OVERVIEW
实现上,我采用了空间换时间和实现复杂度的这么一个tradeoff。把每个部分都用一个word来存,这样读取就只要lw就行了,如果到bit级别的话,可能跨越多个byte或者word,那么 我就需要到内存或者cache里面读取更多次,性能就不高了,而且每次移动来移动去的也很烦,所以采用了下面这样的存储方式。

加法和减法运算
我们要先输入,然后把输入的两个浮点数的各个部分,记录到这个value里面,然后把这个value,再转化成两个number来存储,加减法都要指数位对齐(在MIPS中,做加法运算时需要先对齐操作数的指数,与指数大的操作数的小数点对齐,然后再进行加法运算。这个过程称为浮点数规格化,可以保证两个操作数的尾数部分都在相同的位数上进行运算)。然后取符号位来判断,因为我们最后要确定这个浮点数的答案符号,所以我们比较大小,对于减法运算同理。

乘法和除法运算
我的实现是把指数相加,然后有效数相乘,因为我们的有效数只有23位,但是两个整数相乘要hi lo,两个register,因为精度问题,我们只要高位的hi,
- 通过jal指令调用in_put函数从键盘输入两个浮点数,并将它们以IEEE 754的二进制表示转换后存储在内存中。
- 通过jal指令调用input_change_to_value函数将两个浮点数的符号,指数和尾数分别提取出来存储在内存中。
- 通过jal指令调用value_change_to_number函数将两个浮点数的指数与尾数转化为有效值(尾数+隐含前导1)与指数(Exp-127)并分别存储在指定的内存位置中。
- 依次从内存中加载第一个数的有效值、第二个数的有效值、第一个数的指数、第二个数的指数和两个数的符号位。通过判断除数是否为0来决定程序执行流程。
- 对两个数的指数进行比较,如果第一个数的指数大于等于第二个数的指数,则执行dividegreater操作,否则执行dividelower操作。
- dividegreater操作使用相减的方法计算出商的有效值并将其存储在t8寄存器中,同时t8寄存器中,同时t8对应的位置置1,计数变量$t5加1。
- dividelower操作将第一个数左移1位,t8左移1位,计数变量t8左移1位,计数变量t5加1。
- 通过比较t5和24的大小来决定是否退出循环。如果t5和24的大小来决定是否退出循环。如果t5小于24,则返回到步骤5继续执行,否则跳转到dividebreakout。
- 将计算出的商的有效值存储在指定的内存位置中,并将商的指数计算出来存储在内存中。
- 如果两个数的符号相同,则将结果的符号位设为正;否则设为负。
- 跳转到add_or_sub_output函数对结果进行输出。
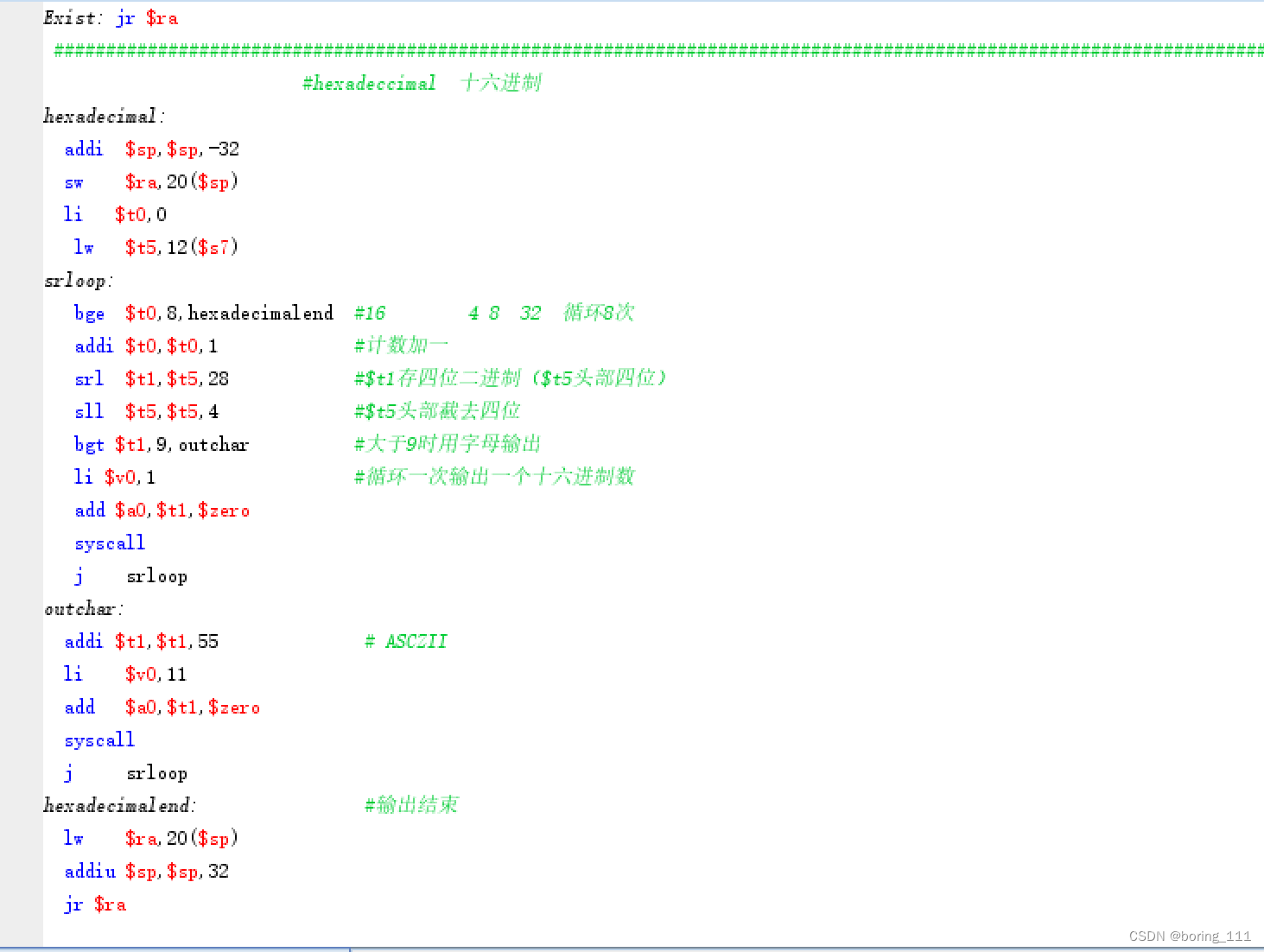
MIPS 汇编代码,包含三个函数 decimal、binary 和 hexadecimal,分别用于将输入的二进制浮点数转换为十进制、二进制和十六进制格式输出。
decimal 函数从内存中读取一个 32 位 IEEE754 格式的浮点数,将其转换为十进制格式并输出。具体实现方法是将读取到的浮点数加载到协处理器1的寄存器 f12 中(这里使用了 MIPS 架构的协处理器1,它用于浮点运算),然后使用系统调用 `syscall` 和 `f12中(这里使用了MIPS架构的协处理器1,它用于浮点运算),然后使用系统调用‘syscall‘和‘v0` 寄存器指定的输出函数来输出 $f12 寄存器中的浮点数。
binary 函数同样从内存中读取一个 32 位 IEEE754 格式的浮点数,并将其转换为二进制格式输出。具体实现方法是利用二进制的性质,从浮点数的头部开始逐位取出二进制数,并将其转换为字符输出。循环次数为32次(因为一个32位的二进制数有32位)。在循环中,首先从内存中读取浮点数,然后利用掩码和移位操作将浮点数的头部四位取出来,保存到寄存器 $t1 中;接着将浮点数的头部截去四位,以便下一轮循环中取出下一个二进制位。然后,将 $t1 中的值转换成字符输出。如果 $t1 大于 9,则需要将其转换为 A~F 中的一个字符。
hexadecimal 函数从内存中读取一个 32 位 IEEE754 格式的浮点数,并将其转换为十六进制格式输出。具体实现方法类似于 binary 函数,不同之处在于每次循环中取出的是 4 个二进制位,对应于一个十六进制数字。然后将这个数字转换成字符输出。如果数字大于 9,则需要将其转换为 A~F 中的一个字符