目录
1. 不同的二叉搜索树 🌟
2. 二叉树的锯齿形层序遍历 🌟🌟
3. 二叉树的右视图 🌟🌟
🌟 每日一练刷题专栏 🌟
Golang每日一练 专栏
Python每日一练 专栏
C/C++每日一练 专栏
Java每日一练 专栏
1. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
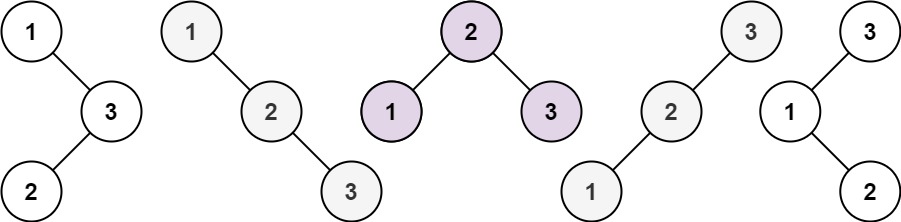
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
以下程序实现了这一功能,请你填补空白处内容:
```c++
#include <stdc++.h>
using namespace std;
class Solution
{
public:
int numTrees(int n)
{
vector<int> sum(n + 1);
sum[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 0; j < i; j++)
{
___________________;
}
}
return sum[n];
}
}
```
出处:
https://edu.csdn.net/practice/26740038
代码1: 动态规划
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n+1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < i; j++) {
dp[i] += dp[j] * dp[i-j-1];
}
}
return dp[n];
}
};
int main()
{
Solution s;
cout << s.numTrees(3) << endl;
cout << s.numTrees(11) << endl;
return 0;
}输出:
5
58786
题目本质:卡特兰数
卡特兰数,又称明安图数、明安图-卡特兰数,是组合数学中一个常出现于各种计数问题中的数列。1730年,中国清代蒙古族数学家明安图比卡特兰更早使用了卡特兰数,在发现三角函数幂级数的过程中,见《割圜密率捷法》。后来他的学生在1774年将其完成发表。其前几项为(从第0项开始):1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
卡特兰数满足以下递推关系:

代码2: 递归实现
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int numTrees(int n) {
if (n < 2) {
return 1;
}
int res = 0;
for (int i = 0; i < n; i++) {
res += numTrees(i) * numTrees(n-i-1);
}
return res;
}
};
int main()
{
Solution s;
cout << s.numTrees(3) << endl;
cout << s.numTrees(11) << endl;
return 0;
}代码3: 左右双递归
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int numTrees(int n) {
if (n == 0) {
return 1;
}
int res = 0;
for (int i = 1; i <= n; i++) {
int left = numTrees(i - 1);
int right = numTrees(n - i);
res += left * right;
}
return res;
}
};
int main()
{
Solution s;
cout << s.numTrees(3) << endl;
cout << s.numTrees(11) << endl;
return 0;
}2. 二叉树的锯齿形层序遍历
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层序遍历如下:
[ [3], [20,9], [15,7] ]
出处:
https://edu.csdn.net/practice/25223618
代码:
#include <bits/stdc++.h>
#define null INT_MIN
using namespace std;
struct TreeNode
{
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution
{
public:
vector<vector<int>> zigzagLevelOrder(TreeNode *root)
{
if (!root)
return {};
vector<vector<int>> res;
vector<int> temp;
int level = 0;
queue<pair<TreeNode *, int>> q;
q.push(pair<TreeNode *, int>(root, 0));
while (!q.empty())
{
TreeNode *node = q.front().first;
level = q.front().second;
q.pop();
if (res.size() < level)
{
if (level % 2 == 0)
reverse(temp.begin(), temp.end());
res.push_back(temp);
temp.clear();
}
temp.push_back(node->val);
if (node->left)
q.push(pair<TreeNode *, int>(node->left, level + 1));
if (node->right)
q.push(pair<TreeNode *, int>(node->right, level + 1));
}
if (level % 2 != 0)
reverse(temp.begin(), temp.end());
res.push_back(temp);
return res;
}
};
TreeNode* buildTree(vector<int>& nums)
{
if (nums.empty()) return nullptr;
TreeNode *root = new TreeNode(nums.front());
queue<TreeNode*> q;
q.push(root);
int i = 1;
while(!q.empty() && i < nums.size())
{
TreeNode *cur = q.front();
q.pop();
if(i < nums.size() && nums[i] != null)
{
cur->left = new TreeNode(nums[i]);
q.push(cur->left);
}
i++;
if(i < nums.size() && nums[i] != null)
{
cur->right = new TreeNode(nums[i]);
q.push(cur->right);
}
i++;
}
return root;
}
string vectorToString(vector<int> vect) {
stringstream ss;
ss << "[";
for (size_t i = 0; i < vect.size(); i++)
{
ss << (vect[i] == null ? "null" : to_string(vect[i]));
ss << (i < vect.size() - 1 ? ", " : "");
}
ss << "]";
return ss.str();
}
int main()
{
Solution s;
vector<int> nums = {3,9,20,null,null,15,7};
TreeNode* root = buildTree(nums);
cout << "[" << endl;
for (auto vec: s.zigzagLevelOrder(root))
cout << vectorToString(vec) << endl;
cout << "]" << endl;
return 0;
}输出:
[
[3]
[20, 9]
[15, 7]
]
3. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
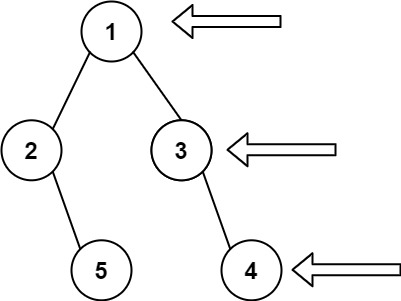
输入: [1,2,3,null,5,null,4] 输出: [1,3,4]
示例 2:
输入: [1,null,3] 输出: [1,3]
示例 3:
输入: [] 输出: []
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
代码:
#include<iostream>
#include<sstream>
#include<vector>
#include<queue>
#define null INT_MIN
using namespace std;
struct TreeNode
{
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
TreeNode* buildTree(vector<int>& nums)
{
if (nums.empty()) return nullptr;
TreeNode *root = new TreeNode(nums.front());
queue<TreeNode*> q;
q.push(root);
size_t i = 1;
while(!q.empty() && i < nums.size())
{
TreeNode *cur = q.front();
q.pop();
if(i < nums.size() && nums[i] != null)
{
cur->left = new TreeNode(nums[i]);
q.push(cur->left);
}
i++;
if(i < nums.size() && nums[i] != null)
{
cur->right = new TreeNode(nums[i]);
q.push(cur->right);
}
i++;
}
return root;
}
string vectorToString(vector<int> vect) {
stringstream ss;
ss << "[";
for (size_t i = 0; i < vect.size(); i++)
{
ss << (vect[i] == null ? "null" : to_string(vect[i]));
ss << (i < vect.size() - 1 ? ", " : "]");
}
return ss.str();
}
class Solution
{
public:
vector<int> rightSideView(TreeNode *root)
{
vector<int> ret;
queue<TreeNode *> queues[2];
if (root)
queues[0].push(root);
int i = 0, j = 1, tmp;
TreeNode *p;
while (!queues[0].empty() || !queues[1].empty())
{
while (!queues[i].empty())
{
p = queues[i].front();
queues[i].pop();
if (p->left)
queues[j].push(p->left);
if (p->right)
queues[j].push(p->right);
tmp = p->val;
}
ret.push_back(tmp);
i = (i + 1) % 2;
j = (j + 1) % 2;
}
return ret;
}
};
int main()
{
Solution s;
vector<int> nums = {1,2,3,null,5,null,4};
TreeNode* root = buildTree(nums);
vector<int> inorder = s.rightSideView(root);
cout << vectorToString(inorder) << endl;
return 0;
}输出:
[1, 3, 4]
🌟 每日一练刷题专栏 🌟
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
☸ 主页:https://hannyang.blog.csdn.net/
 | Golang每日一练 专栏 |
 | Python每日一练 专栏 |
 | C/C++每日一练 专栏 |
 | Java每日一练 专栏 |