目录
视频编码流程
DCT变换
Hadamard变换
量化
H264中的DCT变换和量化
H264各模式的DCT变换和量化过程
1、亮度16x16帧内预测块
2,其它模式亮度块
3,色度块
小结
视频编码流程

DCT变换
离散余弦变换
它能将空域信号转换到频率上表示,并能够比较好的去除相关性。
对于图像来说,空域是平时看到的图像,频率是图像做完DCT变换之后的数据。
DCT变换是对残差块做的,通常情况下是在4X4的子块上进行变换的
二维DCT变换公式如下,f(i,j)是指第(i,j)位置点的信号值,N是采样点的总个数
计算公式:
其中
其中 X为4x4 残差块
A矩阵如下
cos函数有小数,计算速度慢
Hadamard变换
一定程度上粗略的代替 DCT 变换,从而用来简化运算。
计算公式:
没有浮点运算,计算速度快
量化
将图像块变换到频域后,AC系数比较多,一般幅值比较小,通过去除一些AC系数,达到压缩的目的。
量化公式
z是量化后的系数;y是变换系数;round函数是四舍五入
QP与QStep之间有转换关系
通常QStep值越大,DC系数和AC系数被量化成0的概率越大,压缩程度越大。
值太大会造成一个个块状效应,严重的时候出现马赛克。
值小的话,压缩程度比较小,图像失真比较小,码流比较大
H264中的DCT变换和量化
H264为了减少这种浮点运算带来的误差,将DCT变换成整数变化,DCT变换中的浮点运算和量化过程合并,这样就只有一次浮点运算过程。
H264的整数变化和量化,公式如下:
将DCT变换一步步修改为整数变换,最后H264的DCT变换变成了整数变换。
量化
变成
H264各模式的DCT变换和量化过程
1、亮度16x16帧内预测块
亮度16x16,首先被划分成16个4x4的小块做整数变化。变化之后将16个4x4小块的DC系数都拿出来,组成4x4的DC块,再对这个4x4的DC进行Hadamard变换。然后,再总体进行量化操作。
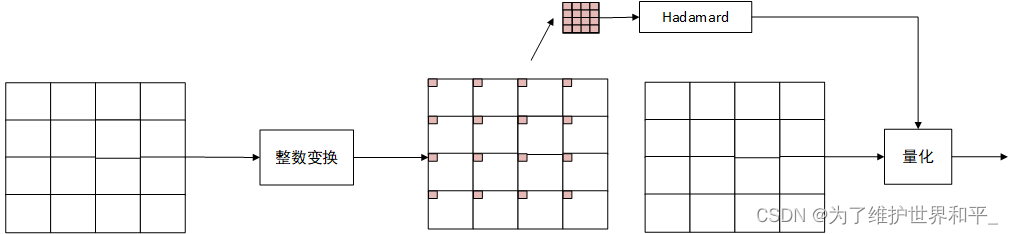
2,其它模式亮度块
对于除亮度16x16帧内预测块之外的其它亮度块,都是直接划分成4x4的块进行整数变化,之后再进行量化操作。
3,色度块
对于YUV420图像,色度块大小是8x8,现将8x8色度块划分成4个4x4的小块做整数变换。变换之后将4个小块的DC系数拿出来,组成2x2的DC块,再对这个2x2的DC块进行hadamard变换。最后总体进行量化操作。
小结
DCT变化主要是将图像从空域转换到频域,并将图像的高频和低频信息分离开来。高频信息数据多,但是幅值比较小,在高频信息量化过程中能够比较容易被量化成0,这样达到压缩的目的。






![[附源码]计算机毕业设计springboot高校流浪动物领养网站](https://img-blog.csdnimg.cn/b74a57108a924235853f9c868a770ed8.png)


![[附源码]计算机毕业设计springboot高校学生摄影作品展示平台](https://img-blog.csdnimg.cn/72ee6c7b7bac4876b608f6b112b741ee.png)