题目

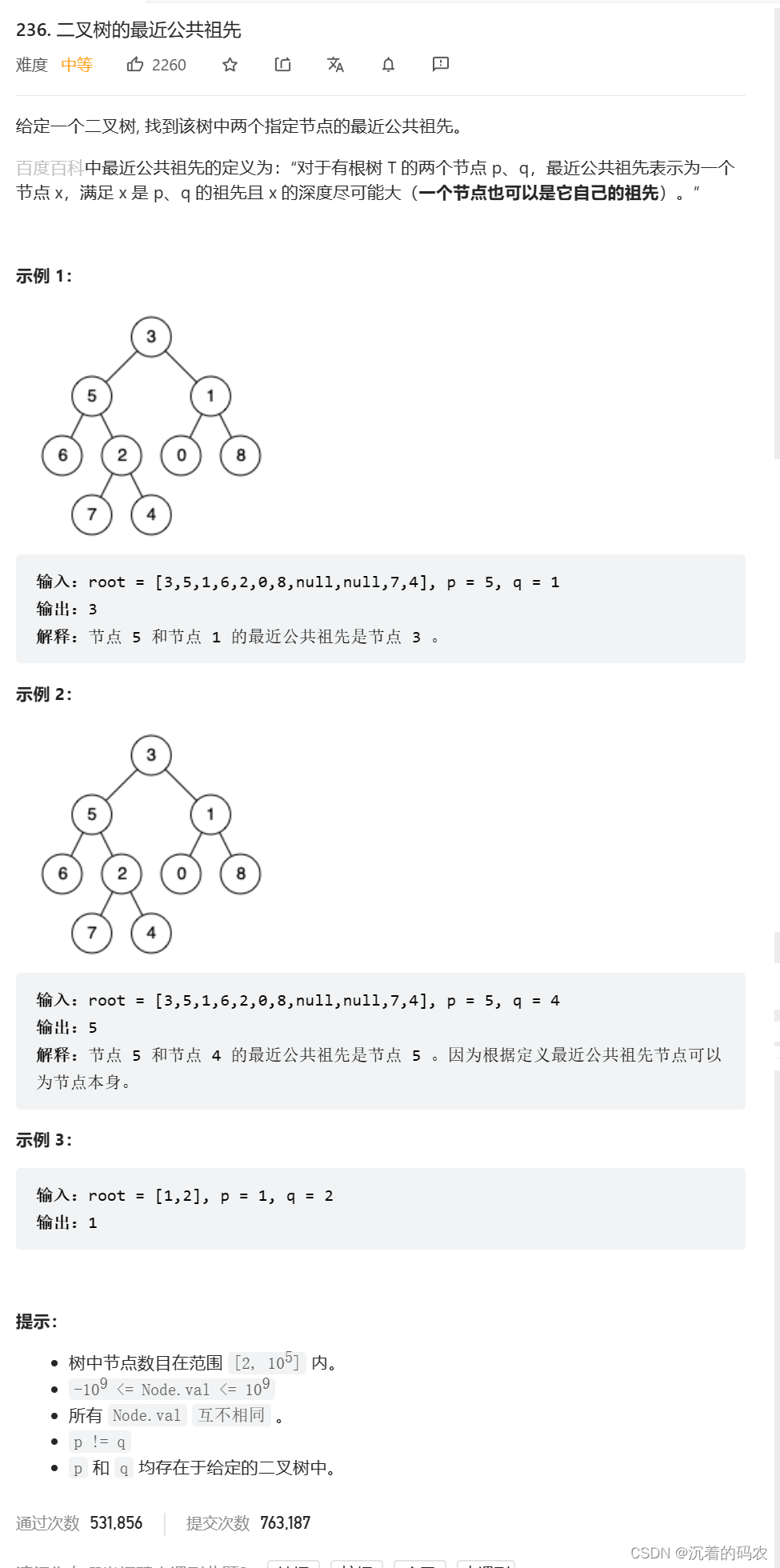
在这里插入图片描述

思路1

给我们两个二叉树中的节点找出里面的最近公共祖先

首先我们要分析p q 两点有哪些位置关系

p q在根节点的两侧

此时最近公共祖先就是根节点
在根节点一侧

此时两个节点都在根节点左侧此时可以递归二叉树让root.left成为根节点也就是图中5的位置此时p q节点又成了第一种情况
p或q其中一个是根节点
此时根节点就是最近公共祖先

思路2

我们要找两个节点的公共祖先也就是说从根节点开始走会在一个地方分岔再走各自的最短路
**如果我们的节点有一个指向上一个节点的值我们原路返回在两个节点第一次相遇的地方就是他们的最小公共节点 **
**但是这里还有一个问题我们怎么能知道两个节点返回的速度呢？也就是说我们不知道两个节点到根节点的举例的长度是多少 **
解决办法是：因为在分叉前两个节点所走的路程是相同的知道分叉后才有可能出现不相同的情况如果我们判断出两段路径的长度谁长让长的路径走长短路径的差值步这样两个节点到根节点的距离就相同了他们以同样的速度返回就会在公共祖先处相遇

那么问题是二叉树并没有给我们找父节点的索引我们怎么能找到父节点呢？
这里就要使用我们另一个数据结构——栈我们把每次的路径保存在栈中返回的时候直接弹出栈顶元素即可

问题就转变为怎样找到两个节点到根节点的最短路径我们可以采用遍历二叉树的方法来操作

//找节点到root的最短路径 并放在栈中
//我们采用的是从根节点向下查找我们要获取路径的节点；
public boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack){
        if(root == null){
            return false;//如果节点为空
        }
        stack.push(root);
        //不管三七二十一 压入栈中
        if(root == node){
            return true;
        }//如果根节点等于 我们要找的节点
        boolean ret = getPath(root.left, node, stack);
        //遍历左树 找节点
        if(ret == true){
            return true;
            //如果ret == true 说明此时我们找到了 直接返回true；
        }
		//左树没找见从右树找
        boolean ret2 = getPath(root.right, node, stack);
        if(ret2 == ture){
            return true;
        }
        //找到了返回true

 		//如果左树和右树都没有找到
 		//弹出栈顶元素 因为我们不论是不是要的路径都压入栈 此时不正确就要弹出
        stack.pop();
        return false;
        //表示这个路径没有我们要找的节点
    }

我们把关键的逻辑写了之后其余部分就比较简单

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null){
            return null;
        }

        Stack<TreeNode> s1 = new Stack<>();
        Stack<TreeNode> s2 = new Stack<>();
        getPath(root,p,s1);
        getPath(root,q,s2);
        //创建两个栈 并且分别把p和q的路径存储到栈中

        int size1 = s1.size();
        int size2 = s2.size();
        //求出长度

		//让路径长的栈先走差值步 
        if(size1 > size2){
            int size = size1 - size2;
            while(size != 0){
                s1.pop();
                size--;
            }
        }else{
            int size = size2 - size1;
            while(size != 0){
                s2.pop();
                size--;
            }
        }

		//此时在一起走 如果相同 则返回
        while(!s1.empty() && !s2.empty()){
            TreeNode temp1 = s1.pop();
            TreeNode temp2 = s2.pop();
            while(temp1 == temp2 ){
                return temp1;
            }
        }

        return null;
    }

    public static boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack){
        if(root == null){
            return false;
        }
        stack.push(root);
        if(root == node){
            return true;
        }
        boolean ret = getPath(root.left, node, stack);
        if(ret == true){
            return true;
        }

        boolean ret2 = getPath(root.right, node, stack);
        if(ret2 == true){
            return true;
        }
        stack.pop();
        return false;
    }
}

代码

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null){
            return null;
        }//如果为空树 直接返回

        if(p == root || q == root){
            return root;
        }
        //如果p或q为根节点是第三种情况 直接返回根节点
        TreeNode leftRet = lowestCommonAncestor(root.left,p,q);
        TreeNode rightRet = lowestCommonAncestor(root.right,p,q);
		//递归左树和右树
        if(leftRet != null && rightRet != null){
            return root;
            //如果一个在个根节点左侧 一个在右侧返回根节点 对应第二种情况
        }else if(leftRet != null){
            return leftRet;
            //如果右树不包含节点 直接返回左根节点
        }else{
            return rightRet;
            //反之返回右根节点
        }
    }
}