动态规划 — 电线布设
题目描述
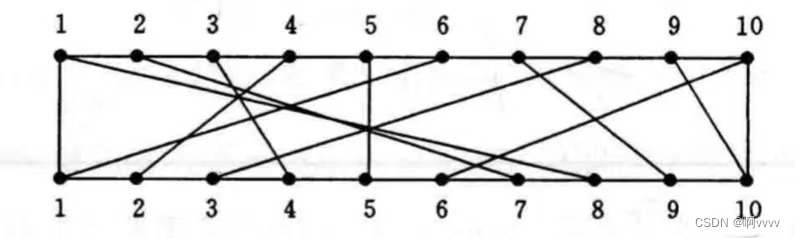
说是话,刚看到也是很懵逼,不想交子集是什么?乱七八糟的连线。
其实仔细想想后,觉得题目应该是说给定了这些点的连接端点,然后从他给的连线中选择出不想交的且条数最多的连线,如下面的例子便是其中的一个最大不相交子集。
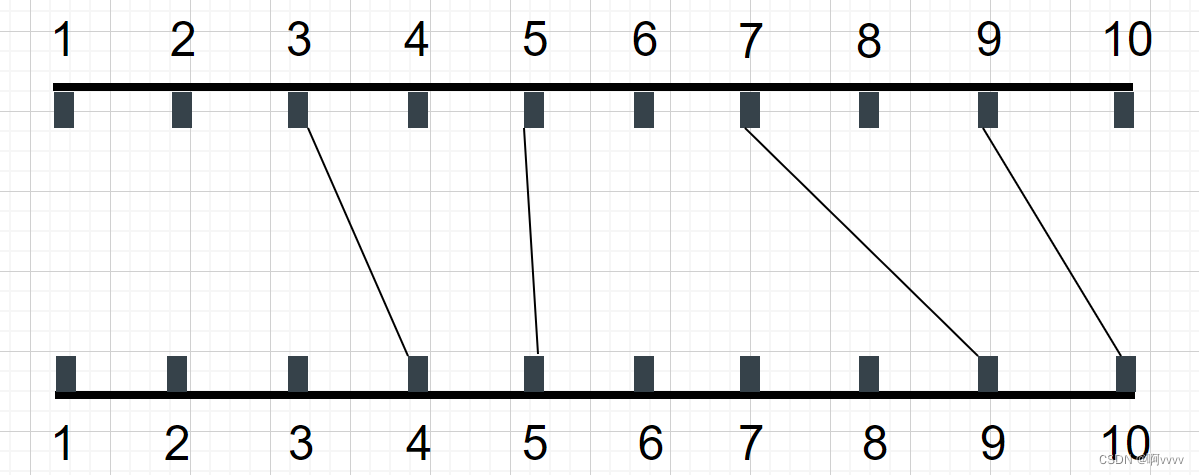
终点数组 end[i] = {0,8,7,4,2,5,1,9,3,10,6};
解决思路,采用动态规划的方式
dp[ i ] [ j ] :表示到达端点i 时,最大不相交子集个数
i :表示 从 1 - N的起点
j :表示 终点
递推式:
当 i == 1时,
如果 j < end[1],当前最大不相交子集为空 dp[ 1 ] [ j ] = 0
如果 j >= end[1],当前最大不相交子集只有一条连线 dp[ 1 ] [ j ] = 1
当 i > 1时,
如果 j < end[i] ,表明当前端点连线还未加入集合 dp[ i ] [ j ] = dp [ i -1 ] [ j ]
如果 j >= end[i],判断当前连线能否加入最大不相交子集 dp [ i ] [ j ] = Math.max(dp [ i - 1 ] [ j ] , dp [i - 1] [ end[ i ] - 1] + 1 )
其实写到dp [ i ] [ j ] = dp [i - 1] [ j ] 还能理解,但是dp [ i ] [ j ] = Math.max(dp [ i - 1 ] [ j ] , dp [i - 1] [ end[ i ] - 1] + 1 ) 怎么去理解?
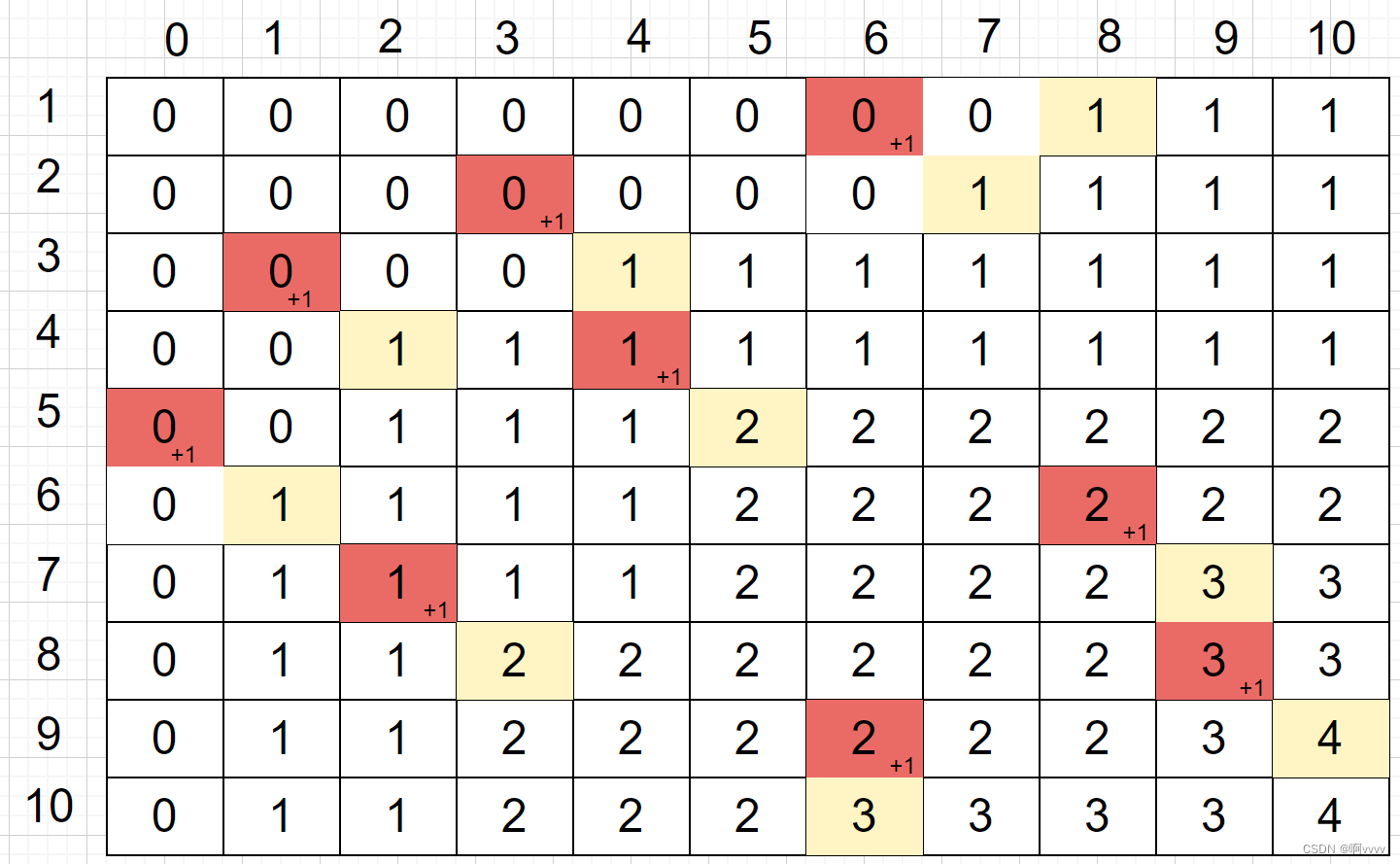
看这个最终填表图

比较的是左上角 与 从上一行继承下来的值, 与 dp [i - 1] [ end[ i ] - 1] + 1 比较是看 最大不相交集合中 有多少条线与 当前线不相交
填表过程
初始化

第二行
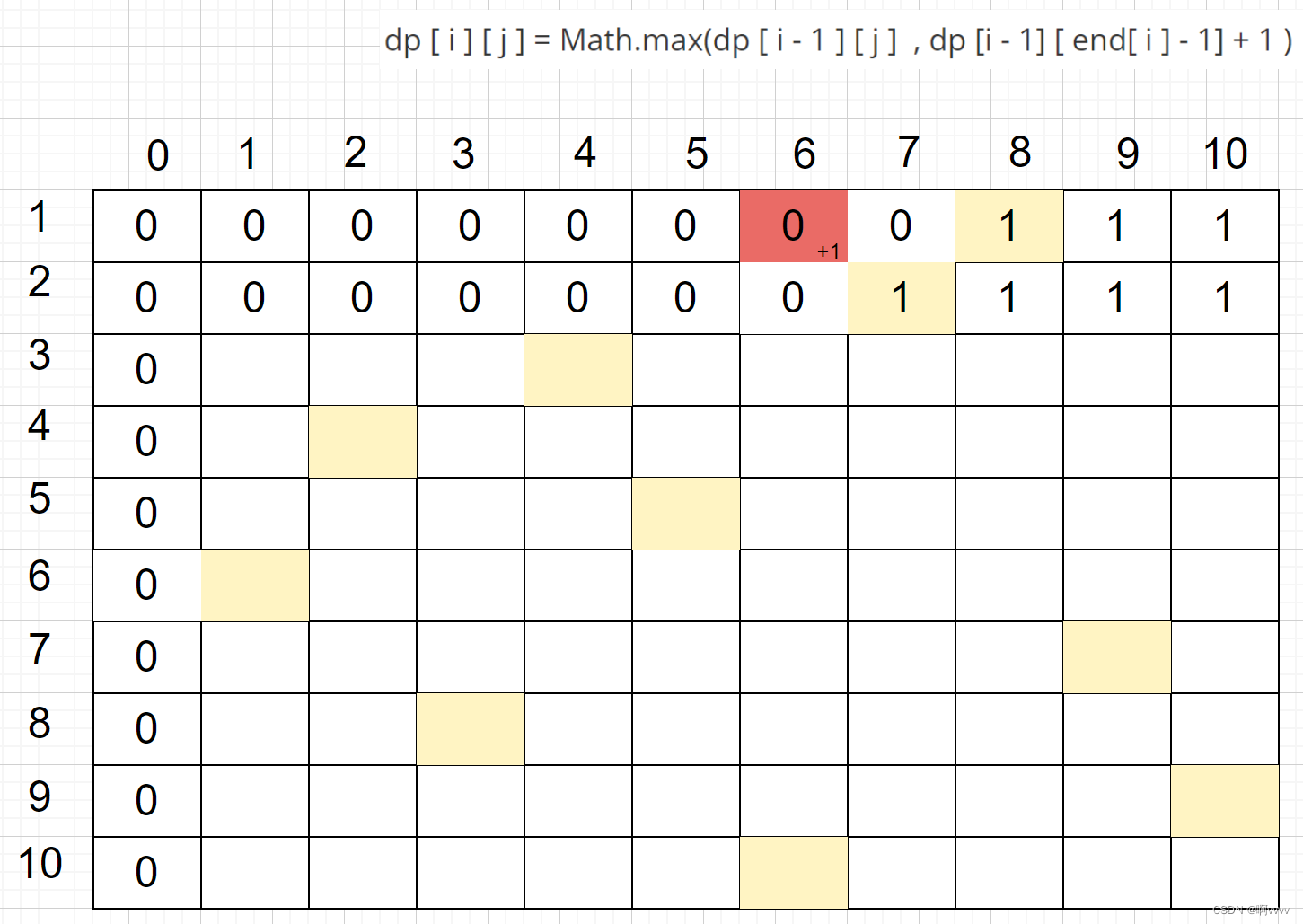
第三行
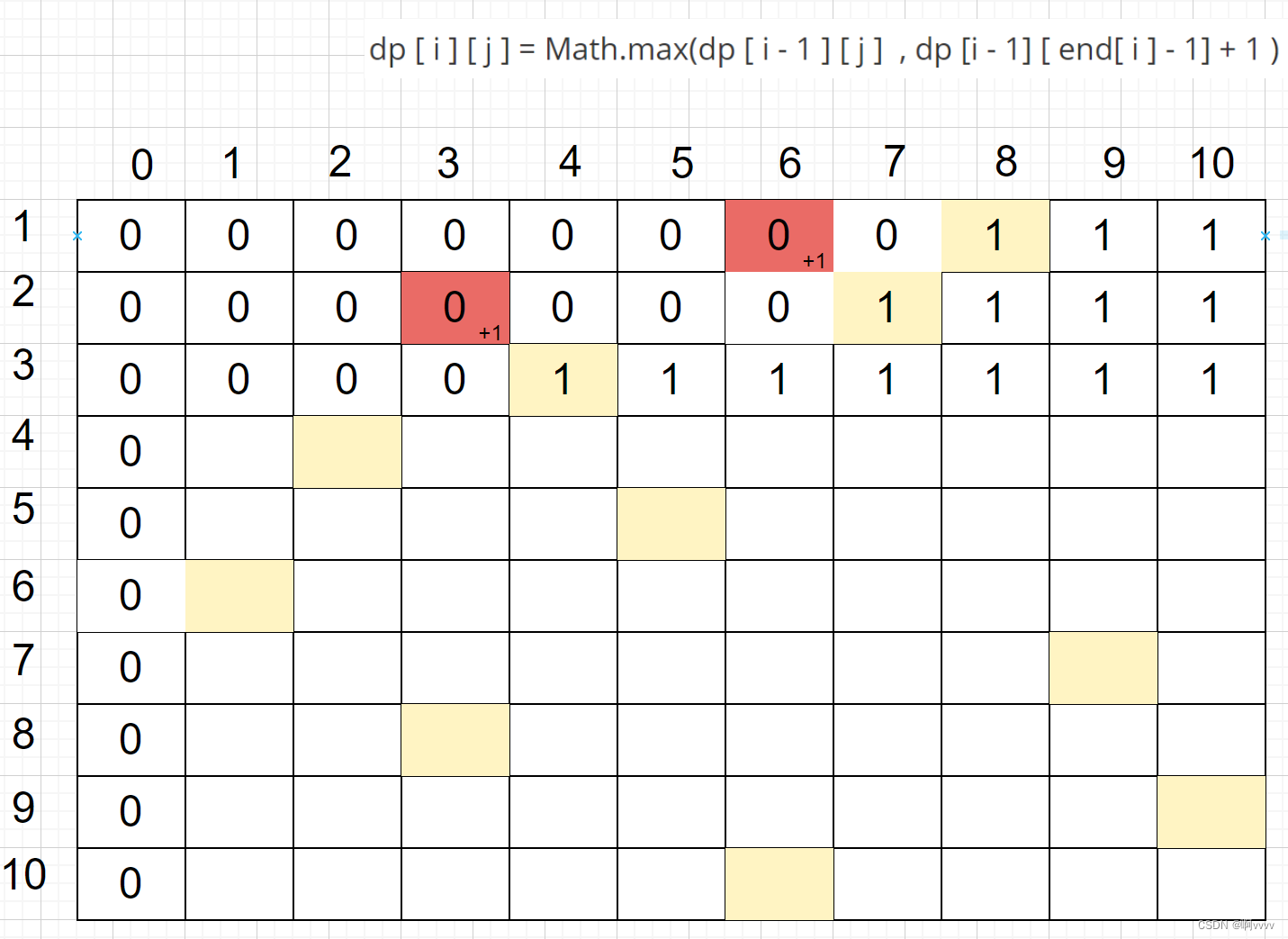
第四行
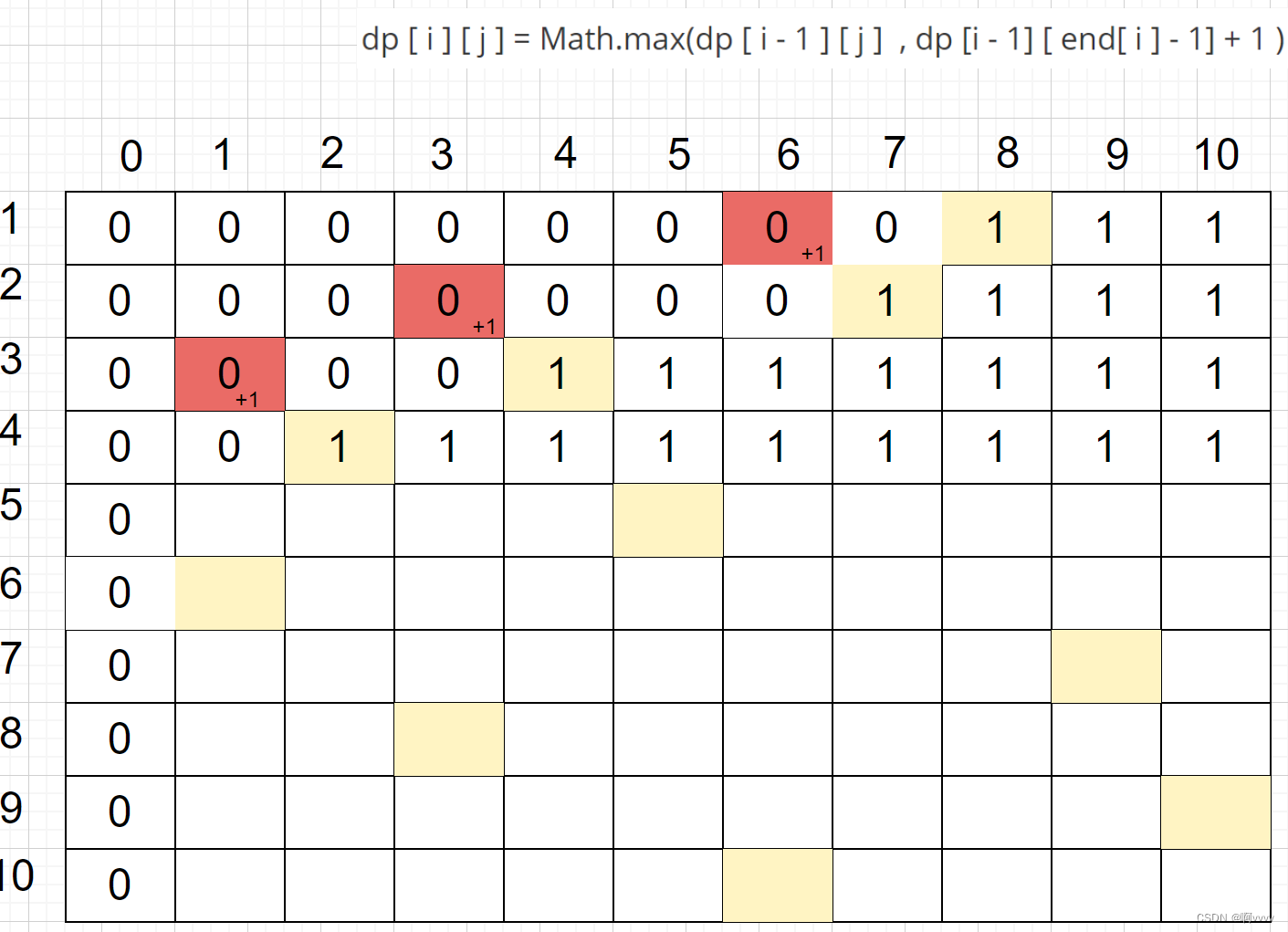
第五行
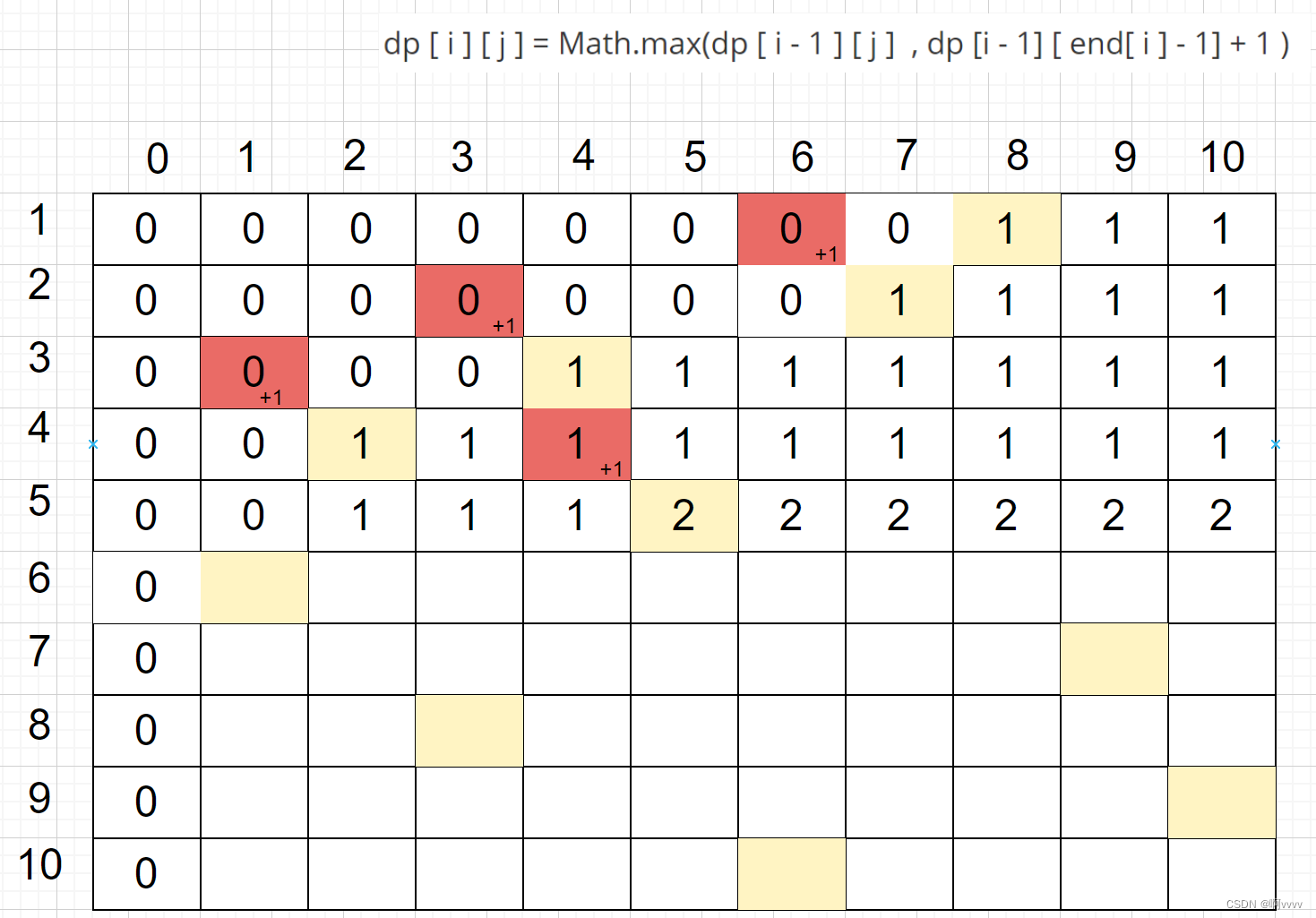
第六行
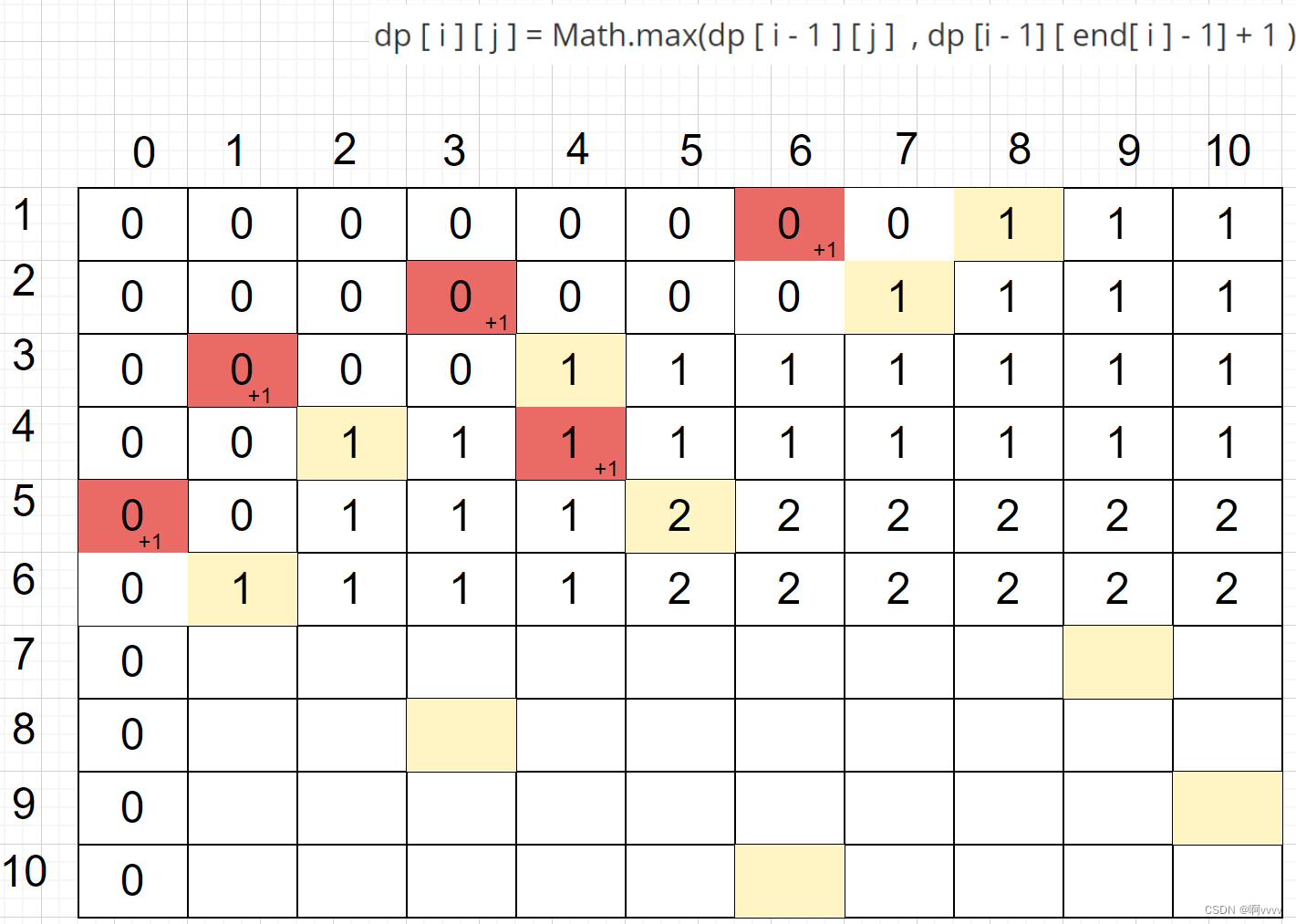
第七行
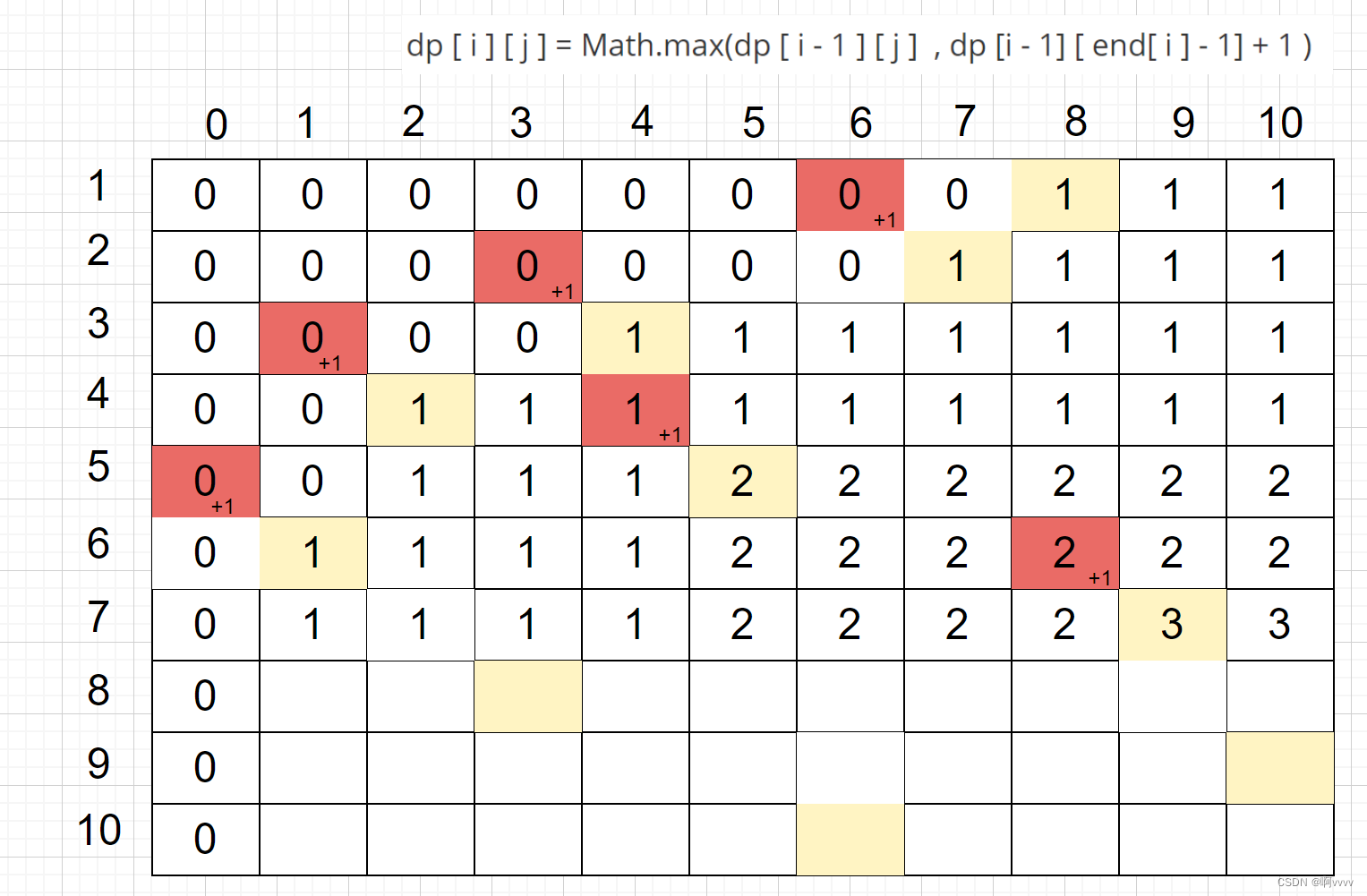
第八行
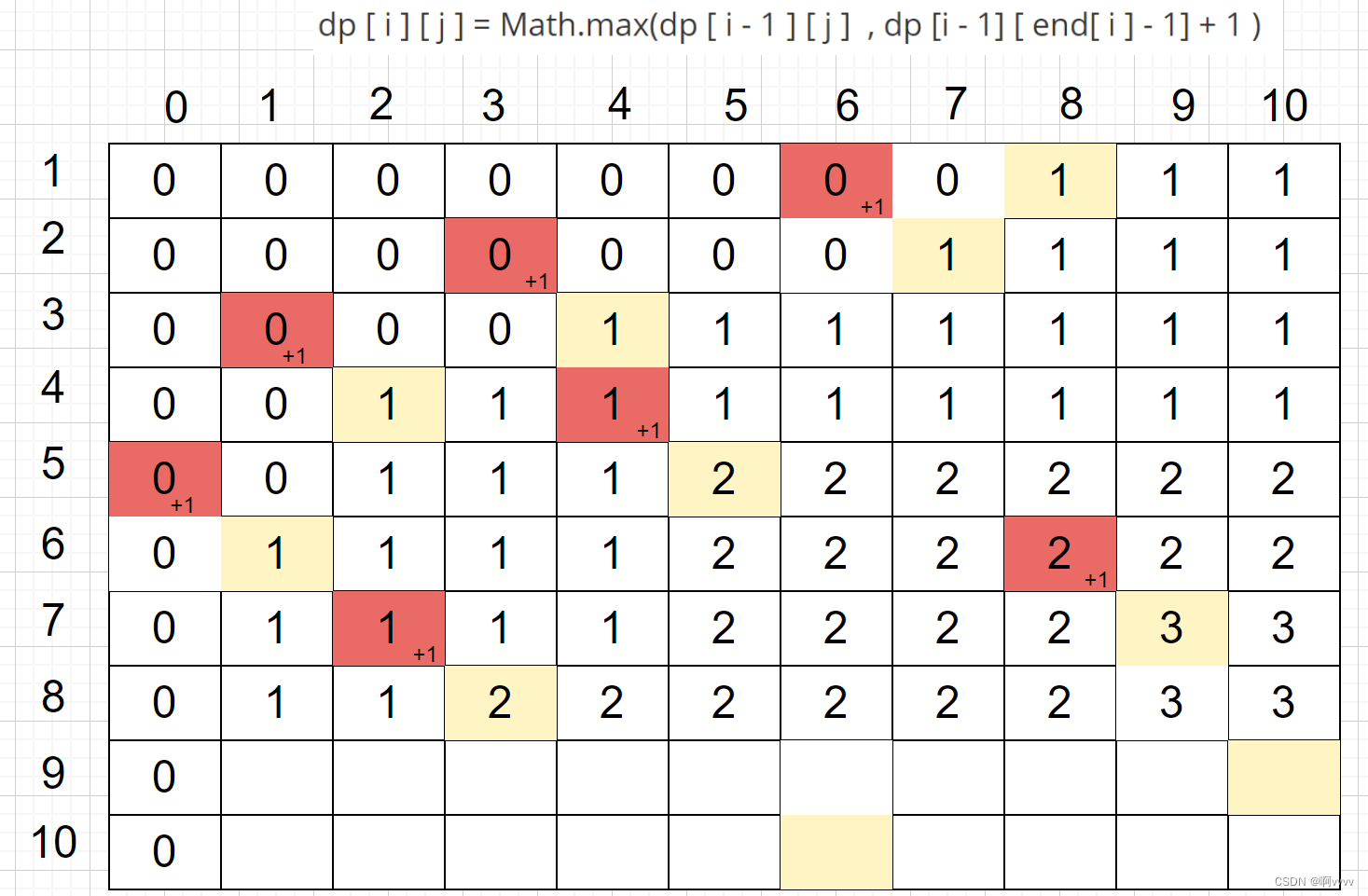
第九行
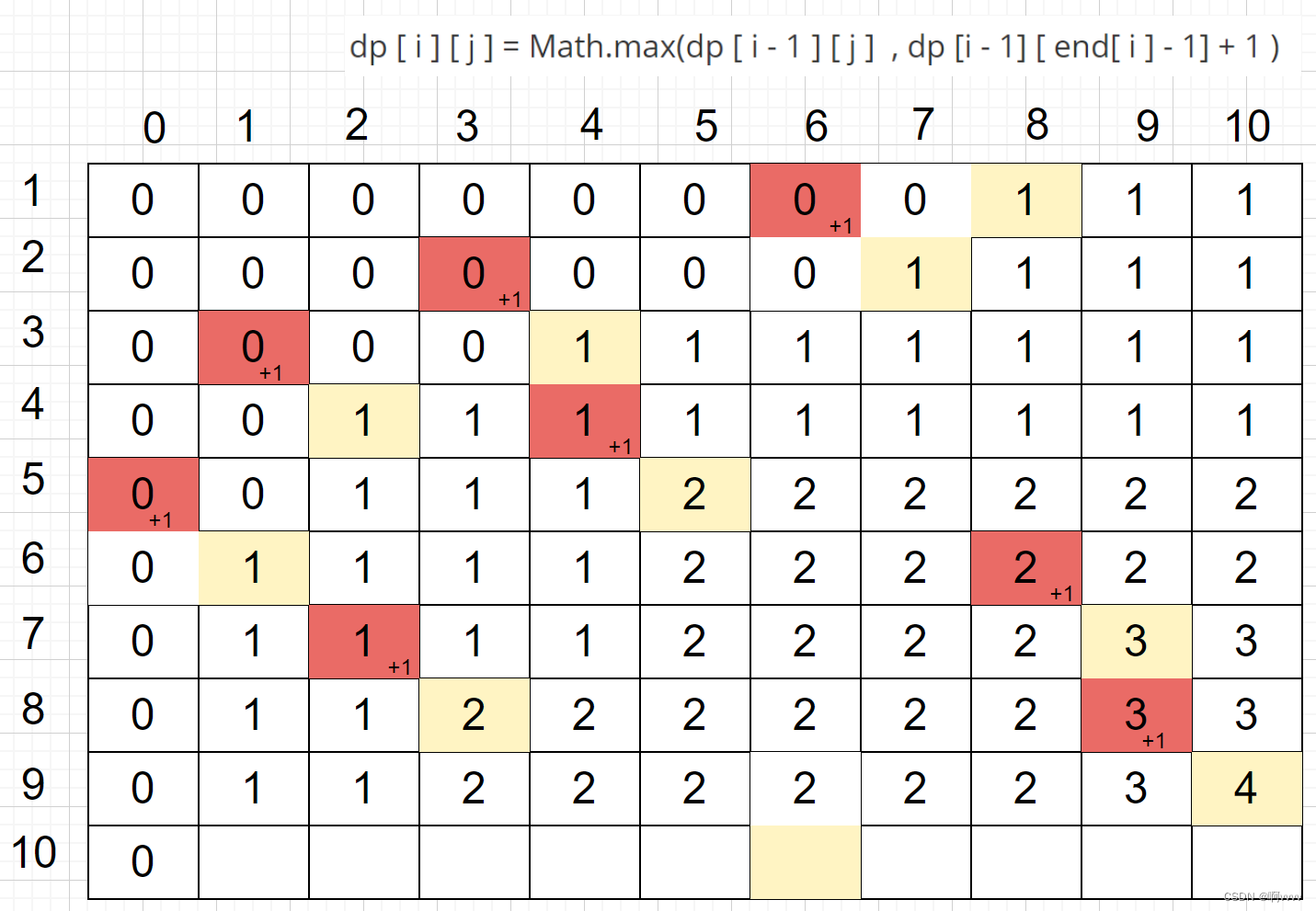
第十行
Java代码
public static void main(String[] args) {
//连线端点
int[] end = {0,8,7,4,2,5,1,9,3,10,6};
//i -- > 表示上端点个数 j --> 表示下端点的个数
//初始化,只有第一个端点时
/**
* dp[i][j]
* i -- > 表示上端点个数 j --> 表示下端点的个数
* i == 1时
* j < end[i] 时
* dp[i][j] = 0
* j >= end[i]时
* dp[i][j] = 1
* i > 1时
* j < end[i] 时 (当前端点代表的线没有被加进集合)
* dp[i][j] = dp[i-1][j]
* j >= end[i]时 (判断当前端点代表的线是否能够被加进来)
* dp[i-1][j] 不能被加进来
* dp[i-1][end[i] - 1] + 1 可以被加进来
* dp[i][j] = Math.max(dp[i-1][j],dp[i-1][end[i] - 1] + 1);
*/
int N = end.length;
int[][] dp = new int[N][N];
//在第一个端点头尾连起来的时候,连线的个数都是0
for(int i = 0; i < end[1]; i++){
dp[1][i] = 0;
}
//超过了端点,证明有一个线被加了进来
for(int i = end[1]; i < N; i++){
dp[1][i] = 1;
}
//最优子结构
//每一个端点前的最大个数 为 上一个端点的最大个数 + 1
for(int i = 2; i < N; i++){
//在到自己连线处时,最大不相交子集为上一个端点存储的值
System.arraycopy(dp[i - 1], 0, dp[i], 0, end[i]);
//在到达当前端点时
for(int j = end[i]; j < N; j++){
//判断当前点的线能否被加进来
//加进来 与 不加进来
dp[i][j] = Math.max(dp[i-1][j], dp[i - 1][end[i] - 1] + 1);
}
}
for(int i = 1; i < N; i++){
for(int j = 1; j < N; j++){
System.out.print(dp[i][j] + " ");
}
System.out.println();
}
//根据dp数组获取一种最大不相交子集
List<Integer> res = new ArrayList<>();
int j = N - 1;
for(int i = N - 1; i > 1; i--){
if(dp[i][j] != dp[i-1][j]){
res.add(i);
//换下一个端点
j = end[i] - 1;
}
}
System.out.println(res);
}
//结果
0 0 0 0 0 0 0 0 1 1 1
0 0 0 0 0 0 0 1 1 1 1
0 0 0 0 1 1 1 1 1 1 1
0 0 1 1 1 1 1 1 1 1 1
0 0 1 1 1 2 2 2 2 2 2
0 1 1 1 1 2 2 2 2 2 2
0 1 1 1 1 2 2 2 2 3 3
0 1 1 2 2 2 2 2 2 3 3
0 1 1 2 2 2 2 2 2 3 4
0 1 1 2 2 2 3 3 3 3 4
[9, 7, 5, 3]