AVL 树（自平衡二叉搜索树) 介绍

1. 前言

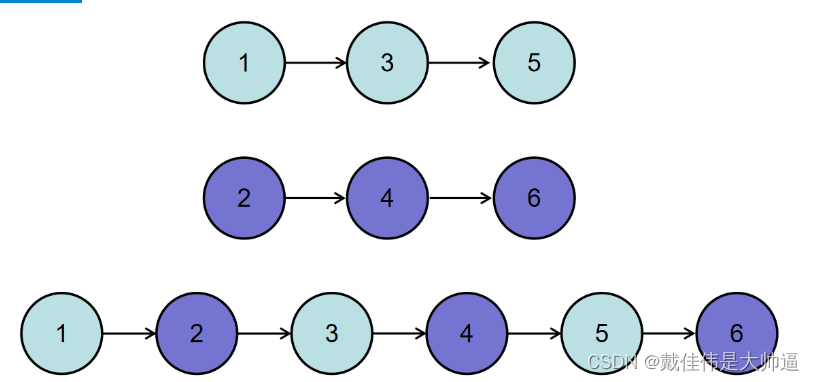
在介绍二叉搜索树的章节中提到，二叉搜索树可能退化为线性链表，失去作为二叉树的各种优势。那么过程中需要维持二叉树的形式，同时左右子树的深度差异可控，如果能实现这两个条件，那么我们称这样的树为自平衡二叉搜索树，由于这类数最早由苏联数学家 Georgy Adelson Velsky 和Landis共同提出，又称之为AVL树。

2. AVL树特征

AVL树的每个结点都需要维护平衡因子，平衡因子的取值范围为-1,0,1，如果所有结点的平衡因子的取值范围都落在-1,0,1范围内，就称这棵树为自平衡二叉搜索树(AVL树)。

观察一个具体例子，下面一棵树就属于一颗AVL 树，因为每个结点的平衡因子都落在-1,0,1范围之内。

下面这棵树就不属于AVL树，因为有的结点的平衡因子为2.

3. AVL树旋转

AVL树可以在元素插入过程中进行旋转处理，确保所有节点的平衡因子落在合理范围之内，如果由于元素插入导致节点的平衡因子落在合理范围之外，那么就需要通过不同模式的旋转操作实现再平衡。值得一提的是，所有的旋转和再平衡操作都发生在递归插入完成之后，也就是从叶子节点开始，不断向上进行不同的调整。

3-1. 左旋操作

左旋操作的对象涉及到两个结点X和Y，当X结点的平衡因子的值超过限制范围的时候，而且右子树比左子树要“重”，这是后就需要把Y作为新的根节点，相当于对X施加左旋的基本操作，操作完成后，整个树满足AVL树的基本要求。

旋转前：

左旋后，Y将作为子树的新根节点，同时满足平衡因子满足AVL树的基本要求。

3-2 右旋操作

右旋操作与左旋操作相反，如上图所示，需要以对Y进行右旋操作，旋转操作之后，二叉树的平衡因子满足AVL树的基本条件和要求，重新回归到AVL树的属性。

3-3 先左旋后右旋

先左旋后右旋的操作会涉及到三个结点，结点Z,X和Y，操作需要自下而上，先对X-Y结点组合施加左旋操作，

操作前：

第一步，左旋操作，

第二步，右旋操作

操作完成后，二叉树重新取得平衡，回归AVL树的属性。

3-4 先右旋再左旋

先右旋再左旋也涉及到三个结点，操作顺序也是自下而上（利用递归回退前的信息属性进行操作），先对靠近底部的子树进行右旋操作，而后再进行左旋处理。

先右旋处理

后左旋处理

4. AVL树的平衡因子和结点高度

平衡因子定义为左子树高度和右子树高度差，由于在旋转过程中需要对平衡因子进行维护和更新，所以需要动态求出每个结点的子树在插入或删除后，本身的平衡因子的变化。结点的平衡因子取决于左右子树的高度差，所以如果需要更新结点的平衡因子，那么首先首先求解本节点两个子树的高度。
$$balance\_factor=height(left\_subtree)-height(right\_subtree);$$

5. AVL树的插入操作

AVL树的插入操作与普通二叉树插入操作基本相同，唯一不同点在于，插入完成后，需要对节点自底而上进行平衡因子的更新及相应的转动操作。这些反转操作必须在插入完成后才能进行，插入前无法进行更新，这就类似单个递归的后续操作，当递归完成后，然后再对相应的信息进行相关操作。

在进行插入操作之前，需要进行对相关的辅助函数进行编写。其中get_height(Node *node)函数返回节点当前的高度，如果节点没有左右子树，节点高度定义为1。

typedef struct Node
{
    int key;
    struct Node *lchild;
    struct Node *rchild;
    int height;
}Node;


int get_height(Node *node)
{
    if(node==NULL)
    {
        return 0;
    }
    else
    {
        return node->height;
    }
}

根据上面的公式，可以求出每个节点的平衡因子，get_balance_factor(Node *node)函数的作用为求出某个节点的平衡因子。

int get_balance_factor(Node *node)
{
    if(node==NULL)
    {
        return 0;
    }
    else
    {
        return (get_height(node->lchild) - get_height(node->rchild));
    }
}

如果要得到某个节点的后继节点，那么就需要使用函数find_successor(Node *node)进行求解，然后返回某个相关的节点。

Node *find_successor(Node *node)
{
    Node *p;

    if(node==NULL)
    {
        return NULL;
    }

    p=node->rchild;

    while(p && p->lchild)
    {
        p=p->lchild;
    }

    return p;
}

如果需要创建新的节点，那么就需要采用函数make_node，创建新的节点，然后返回创建的节点即可。

Node *make_node(int key)
{
    Node *node;

    node=(Node*)malloc(sizeof(Node));
    node->height=1;
    node->lchild=node->rchild=NULL;
    node->key=key;

    return node;
}

左旋操作

Node *left_rotation(Node *node)
{
  	Node *rc;
  	Node *new_node;

  	rc=node->rchild;
  	node->rchild=rc->lchild;
  	rc->lchild=node; //node =rc;
  	new_node=rc;

    // from the bottom to top
  node->height=max(get_height(node->lchild),get_height(node->rchild))+1;

  new_node->height = max(get_height(new_node->lchild), get_height(new_node->rchild)) + 1;

  return new_node;
}

右旋操作

Node *right_rotation(Node *node)
{
    Node *lc;
    Node *new_node;

    lc=node->lchild;
    node->lchild=lc->rchild;
    lc->rchild=node;
    new_node=lc;

    //from the bottom to top
    node->height = max(get_height(node->lchild), get_height(node->rchild)) + 1;

    new_node->height = max(get_height(new_node->lchild), get_height(new_node->rchild)) + 1;

    return new_node;
}

节点插入的函数分析，插入节点的函数当中，出现node->lchild=insert_node(node->lchild,key)表达是，这个表达式的作用是把前一个栈弹出的值赋给node->lchild即可，所以它不需要返回值，只需要赋值即可。

Node *insert_node(Node *node, int key)
{
    int bf; //balance factor;
    if(node==NULL)
    {
        return make_node(key); //create the new node
    }

    if(key < node->key)
    {
        node->lchild=insert_node(node->lchild,key);
    }
    else if(key > node->key)
    {
        node->rchild=insert_node(node->rchild,key);
    }
    else
    {
        return node; //termination condition had been reached;
    }

    //update the balance factor of each node and rebalance the AVL tree
    node->height=max(get_height(node->lchild),get_height(node->rchild))+1;
    bf=get_balance_factor(node);

    if(bf>1 && key < node->lchild->key)
    {
        return right_rotation(node);
    }

    if(bf<-1 && key >node->rchild->key)
    {
        return left_rotation(node);
    }

    if(bf>1 && key > node->lchild->key)
    {
        node->lchild=left_rotation(node->lchild);
        return right_rotation(node);
    }

    if(bf<-1 && key < node->rchild->key)
    {
        node->rchild=right_rotation(node->rchild);
        return left_rotation(node);
    }
    

    return node; //general root node;
}

节点删除函数分析，节点的删除分为三类情况：

如果节点的左子树或右子树为空，那么直接把其右子树或左子树赋给当前节点即可。如果左右子树均不为空，那么就需要找到此节点的后继节点，用后继节点的值替换待删除节点的值，最后把后继节点删除即可，后继节点可以为叶子节点也可以为中间的某个节点。

具体的实现函数为

Node *delete_node(Node *root, int key)
{
    //Deleting the node is the best algorithm we've ever had, it deserves learning
    
    Node* temp;
    int bf;
    
    
    if(root==NULL)
    {
        return root; //failure to find the target node
    }

    if(key < root->key)
    {
        root->lchild=delete_node(root->lchild,key);
    }
    else if(key > root->key)
    {
        root->rchild=delete_node(root->rchild,key);
    }
    else
    {
        if(root->lchild==NULL || root->rchild==NULL)
        {
            temp=(root->lchild?root->lchild:root->rchild);

            if(temp==NULL)
            {
                temp=root;
                root=NULL;
            }
            else
            {
                *root=*temp; //it will equal to left child or righ child;
            }

            free(temp);
            temp=NULL;
        }
        else
        {
            temp=find_successor(root);
            root->key=temp->key;

            //Highlight these application
            root->rchild=delete_node(root->rchild,temp->key); //delete the leaf key
        }
    }

    if(root==NULL) //key steps, if the last node is empty, then return empty
    {
        return root;
    }

    root->height=max(get_height(root->lchild),get_height(root->rchild))+1;

    bf=get_balance_factor(root);

    if(bf>1 &&get_balance_factor(root->lchild)>=0) //>=0;
    {
        return right_rotation(root);
    }

    if (bf > 1 && get_balance_factor(root->lchild) < 0)
    {
        root->lchild=left_rotation(root->lchild);
        return right_rotation(root);
    }


    if(bf<-1 && get_balance_factor(root->rchild)<=0)//<=0
    {
        return left_rotation(root);
    }

    if (bf < -1 && get_balance_factor(root->rchild) >0)
    {
        root->rchild=right_rotation(root->rchild);
        return left_rotation(root);
    }

    return root;
}

5. 小结

要理解AVL算法，关键和核心是理解递归后的处理逻辑，递归后如果需要对子树进行旋转，那么旋转后直接返回即可，否则则需要原来的节点。这里面涉及到比较复杂的递归利用。

不同于严蔚敏《数据结构》，这里实现的算法比较直观，没有《数据结构》里面taller对树的高度的判断，如果有时间将分析严蔚敏版本的AVL树，里面的代码简洁，但是对于删除操作实现，难度很高。

参考资料

https://www.programiz.com/dsa/avl-tree