注意事项:
本题是"区间DP—能量项链"的扩展题,可以先理解下那道题。
本题使用了"高精度乘法"和"高精度加法",可以去这两篇文章看,有详解。
题目:
给定一个具有 N 个顶点的凸多边形,将顶点从 1 至 N 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 N,表示顶点数量。
第二行包含 N 个整数,依次为顶点 1 至顶点 N 的权值。
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N≤50,
数据保证所有顶点的权值都小于10^9
输入:
5
121 122 123 245 231
输出:
12214884
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 55;
int n, w[N]; //w[i]为第i个顶点的权值
vector<int> f[N][N]; //注意这是个三维数组(第三维是用来算高精度),f[l][r]为从l点到r点整个区域内的不相交的三角形的选法,属性为min(三角形权值之和)
//高精度加法
vector<int> add(vector<int> &A, vector<int> &B) {
if (A.size() < B.size()) return add(B, A);
vector<int> res;
int t = 0;
for (int i = 0; i<A.size(); i++) {
t += A[i];
if (i < B.size()) t += B[i];
res.push_back(t % 10);
t /= 10;
}
if (t) res.push_back(t);
return res;
}
//高精度乘法
vector<int> multi(vector<int> &A, LL B) {
vector<int> res;
LL t = 0;
for (int i = 0; i<A.size() || t; i++) {
if (i < A.size()) t += (A[i] * B);
res.push_back(t % 10);
t /= 10;
}
while (res.size() > 1 && res.back() == 0) res.pop_back();
return res;
}
//高精度比较 compare(A < B)?
bool cmp(vector<int> &A, vector<int> &B) {
if (A.size() != B.size()) return A.size() < B.size();
for (int i = A.size()-1; i>=0; i--) {
if (A[i] != B[i]) {
return A[i] < B[i];
}
}
return true;
}
int main() {
//读入
cin >> n;
for (int i = 1; i<=n; i++) cin >> w[i];
//dp (区间长度len -> 左端点l -> 分界线k)
for (int len = 3; len <= n; len++) {
for (int l = 1; l+len-1 <= n; l++) {
int r = l+len-1;
for (int k = l+1; k<r; k++) {
vector<int> new_value;
new_value.push_back(1); //初始化设为1,这样就能计算乘法了
//w[l]*w[k]*w[r]
new_value = multi(new_value, w[l]);
new_value = multi(new_value, w[k]);
new_value = multi(new_value, w[r]);
//f[l][k] + f[k][r]
new_value = add(new_value, f[l][k]);
new_value = add(new_value, f[k][r]);
//f[l][r] = min(f[l][r], new_value)
if (f[l][r].empty() || cmp(new_value, f[l][r])) f[l][r] = new_value;
}
}
}
//f[1][n]为答案,注意存的是高精度,所以要倒着输出一下
for (int i = f[1][n].size()-1; i>=0; i--) cout << f[1][n][i];
return 0;
}
思路:
先来理解讲下题目吧,
在选定两个点后,和剩余的点组成三角形的方案为n-2个(彩铅佬的图):
对于任意一个这样的三角形,都可以用它来划分区间(假设选择1-4-6这个三角形):
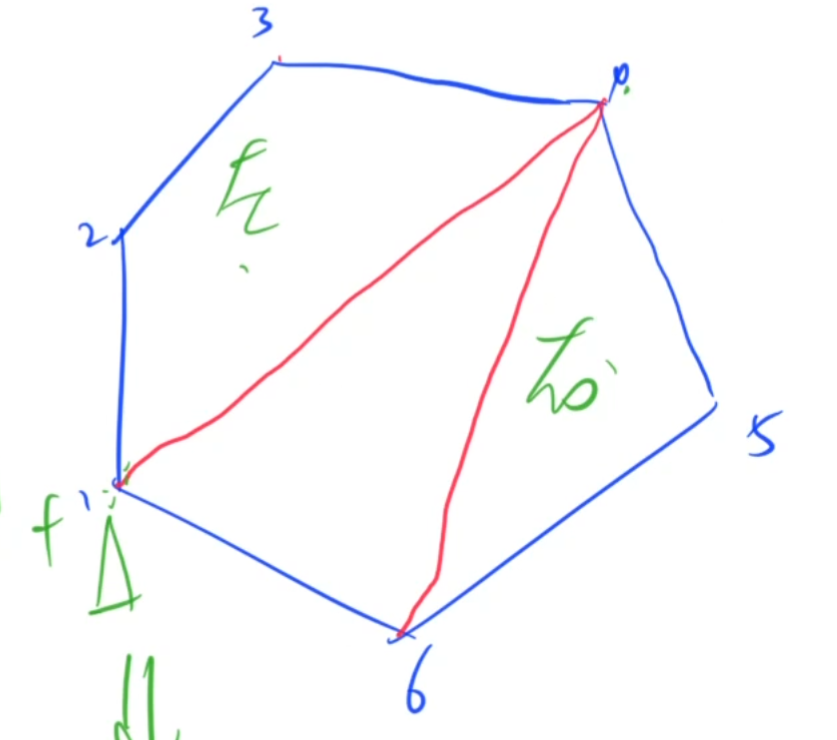
那么左侧区间(1-2-3-4)和右侧区间(4-5-6)互不干扰,
就可以求出左侧区间的最小值f[1][4]和右侧区间的最小值f[4][6]再加上当前w[1]*w[4]*w[6],即为选择(1-4-6)这个三角形的答案。
然后动态规划,还是经典的y式dp法:
1.状态表示
f[L][R]: 当前区域(多边形)的最左侧端点为L,最右侧端点为R的所有方案,
属性为Min(三角形权值的和)。
2.状态计算
以L和R为底边,分界点K为顶点:
左侧区间 + 当前三角形权值 + 右侧区间
f[l][r] = min(f[l][r], f[l][k] + f[k][r] + w[l]*w[k]*w[r])
如果有所帮助请给个免费的赞吧~有人看才是支撑我写下去的动力!
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流