提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、锯齿和反锯齿
- 二、Xiaolin Wu 算法代码
- 1.C#完整代码如下
- 2.举例和测试
- 总结
前言
笔者前几日自己写了个佳明手表表盘的的一个入门级App,模拟指针的。发现在个别角度,指针的锯齿非常拉胯啊,搞得手表不是很美观。准备研究一下直线的反锯齿算法。 试了试GPT,柴先生推荐了几个算法,最后给的是XiaolinWu 的反锯算法,但是因为GPT的一贯的随意性,代码虽然看着好像不错,但是运行不了。只好继续探索该算法的原理,否则它的代码我也看不懂,也改不了。经过一天的研究,终于搞出来了代码,并基本理解了反锯齿算法的核心思想。下面的讨论指的都是基于计算机图形处理范畴,除非特别说明。
一、锯齿和反锯齿
由于显示器的像素是有限集合,因此在分辨率不出特别高的前提下,画一条斜直线,就会出现锯齿现象。如图,下图是windows画图工具经过放大之后的样子:
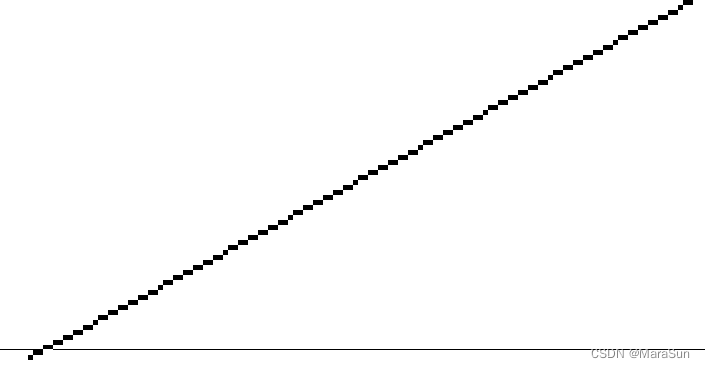
可以看到很明显的锯齿,在某些角度,这个锯齿现象会更加明显。因此如何消除锯齿现象,在要求较高的场合是很重要的。那么,锯齿能消除吗?答案是否定的。为啥呢?因为,这个显示器的特点就是这样。因为它的像素不能很小,在理论上,这些锯齿就是客观存在的。那么就没有办法了吗?实际上计算机图形,只不过是一个示意图而已,因此如果它看起来锯齿消失了,或者变小了,就可以了。没有必要纠结,真正的消失。这也是反锯齿算法依赖的基础。反锯齿算法,就是利用直线和背景的合理混合,使得人眼在观看时,感觉锯齿变小了,甚至有消失的感觉。因此问题的核心,就是怎么实现。
二、Xiaolin Wu 算法代码
本文代码主要是参考了
Wu反走样算法介绍(简单易懂) -Xiaolin Wu’s Algorithm
该博客解释的比较清楚,并给出了伪代码。改代码只能处理 第一象限的小于四十五度的斜线,对水平直线和垂直直线以及其他象限的画线方法都没有处理,但是仍然具有一定的参考价值。为了实用,本文对代码进行了完善,下面代码给出了一个完整的解决方案。
另一个更加详细的解释请参考:
计算机图形学-反走样
1.C#完整代码如下
代码说明:
1、使用了 bitmap 用以完成画点的操作(C#GDI中居然没有画点的函数,只好用图形处理)
2、使用了 Color.FromArgb(alpha, pen_color) 函数实现和背景色彩的 blend(混合?) 运算
3、线段的画法都是从小到大完成的,并对不同斜率的线段,分别采用了不同的坐标。例如小于45度的线段,采用 x 轴从小到大的计算方法;而大于 45度的线段,采用y从小到大的方法。这样做的目的,是防止出现断点。
4、 代码中的Dx 和 Dy 用于匹配3 所说的情况,就是在选择相邻点时是选择横向还是纵向的点。
5、由于是逐个像素计算的,因此直接使用斜率作为累加步长(1*K, 省了了1)
private static void DrawXiaoLnWuLine(Bitmap bitmap ,Color pen_color, PointF p0, PointF p1)
{
PointF p;
float dx, dy;
var Dx = 0;
var Dy = -1;
if (p1.X < p0.X)
{
p = p0;
p0 = p1;
p1 = p;
}
dx = p1.X - p0.X;
dy = p1.Y - p0.Y;
if (dy < 0)
{
Dy = 1;
}
double k = (double)dy / dx, e;
var V1 = p0.X;
var V2 = p1.X;
float val;
if (Math.Abs( k )> 1)
{
Dx = -1;
Dy = 0;
if (p1.Y < p0.Y)
{
p = p0;
p0 = p1;
p1 = p;
}
dx = p1.X - p0.X;
dy = p1.Y - p0.Y;
if (dx < 0)
{
Dx = 1;
}
k = (double)dx / dy;
V1 = p0.Y;
V2 = p1.Y;
}
p = p0;
for (val = V1, e = 0; val < V2; val+=1f)
{
var alpha = (int)(Math.Abs(e) * 255);
Color color = Color.FromArgb(alpha, pen_color);
bitmap.SetPixel( (int)p.X,(int) p.Y, color);
color = Color.FromArgb(255-alpha, pen_color);
bitmap.SetPixel((int)p.X +Dx, (int)p.Y + Dy, color);
e += k;
if (Dy != 0)
{
p.Y += (float)k;
p.X = val;
}
else
{
p.X += (float)k;
p.Y = val;
}
e = e % 1;
}
}
2.举例和测试
测试代码:
var sx = pbx_01.Width / 2;
var sy = pbx_01.Height / 2;
var mHandLen = (int)pbx_01.Width / 2 -4;
var angle = Math.PI / 30 ;
var ex = sx + mHandLen * Math.Cos(angle);
var ey = sy - mHandLen * Math.Sin(angle);
var g1 = pbx_01.CreateGraphics();
pbx_01.BackColor = Color.White;
g1.DrawLine(new Pen(Color.Green), sx, sy, (int)ex, (int)ey);
Bitmap bitmap = new Bitmap(pbx_02.Width, pbx_02.Height);
//SolidBrush brush = new SolidBrush(Color.FromArgb(128, 0, 0, 128));
Graphics g2 = Graphics.FromImage(bitmap);
g2.FillRectangle(Brushes.White, 0, 0, bitmap.Width, bitmap.Height);
var p0 = new Point(sx, sy);
var p1 = new Point((int)ex,(int) ey);
DrawXiaoLnWuLine(bitmap, Color.Green, p1, p0);
pbx_02.Image = bitmap;
该处使用的url网络请求的数据。
测试效果如下:
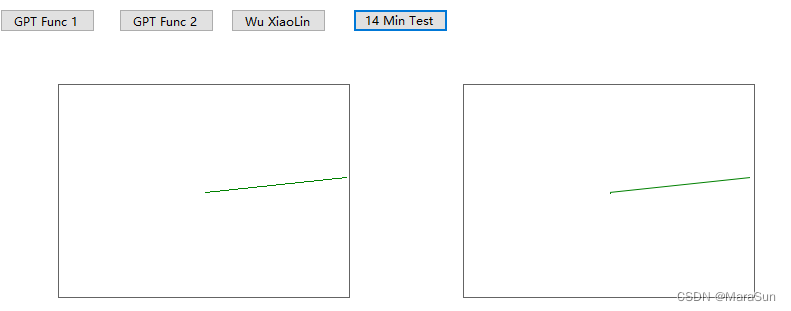
左面是普通画线的效果,右面是使用了XiaolinWu算法之后的效果,可以看出,线段的锯齿得到了较好的弱化。
总结
其实不是所有的线段都要使用这个算法,只有在角度较小或者较大时才比较明显,因此使用时可根据实际情况进行判断,否则效率太低。
MaraSun BJFWDQ
2012-04-27