---

题目要求

给你一个 m x n 的矩阵 M ，初始化时所有的 0 和一个操作数组 op ，其中 ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。

在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。

示例 1:
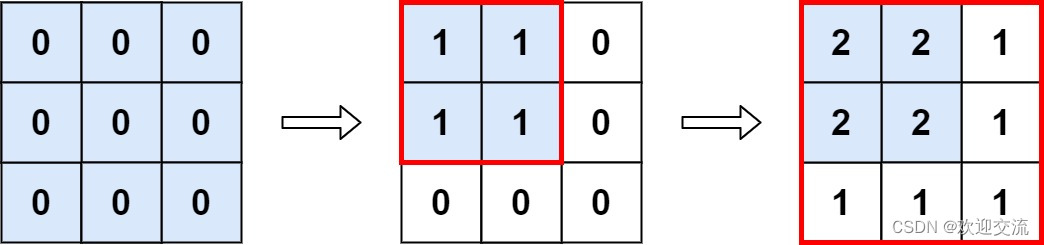输入: m = 3, n = 3，ops = [[2,2],[3,3]]
输出: 4
解释: M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。

示例 2:

输入: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
输出: 4

示例 3:

输入: m = 3, n = 3, ops = []
输出: 9

代码（包含解题思路）

//思路 ： 最大整数的个数一定会出现左上角最小的矩形当中。我们只要求出那个最小矩形的宽和高就可以求出其最大整数的个数
//但是，要考虑示例3这种特殊情况
int maxCount(int m, int n, int** ops, int opsSize, int* opsColSize){
    //注意  最小宽度 对应二维数组某行第二个元素  最小高度对应二维数组中某行第一个元素  
    int minW = n, minH = m;  
    if (opsSize == 0) {  //应对实例三这种情况
        return m * n;
    }

    for (int i = 0; i < opsSize; i++) {
        minW = fmin(ops[i][1], minW);
        minH = fmin(ops[i][0], minH);
    }

    return minW * minH;
}
/*
    时间复杂度为 O(n)
    空间复杂度为 O(1)
*/